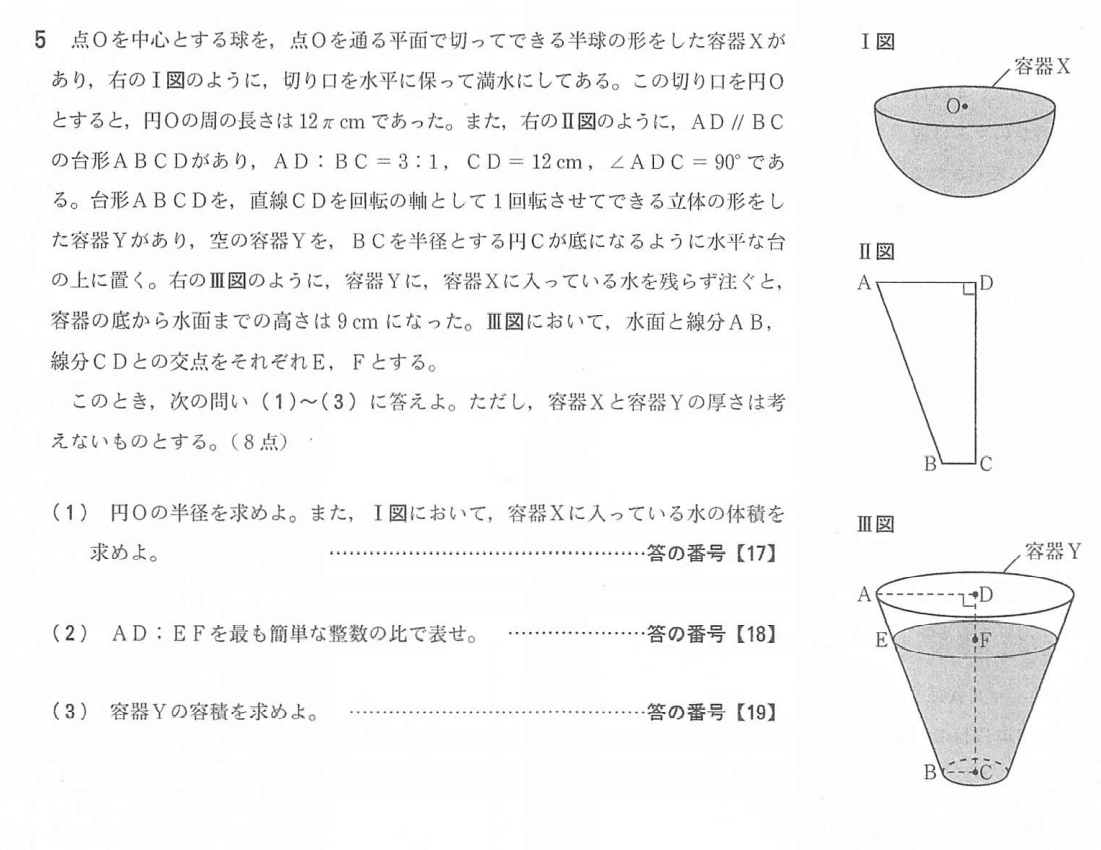
大問3
大問3(3)解答例
(2)で解っていること
\(0 \leq x \leq 4\) のとき \(y=2x^2\)
\(4 \leq x \leq 8\) のとき \(y=16x-32\)
\(x:2 \rightarrow 3\) のとき \(y\)の増加量は
\(2 \times 3^2- 2 \times 2^2=18-8=10\)
この\(6\)倍は \(60\)
\(a=4\) ならば \(x:3 \rightarrow 4\) のとき
\(y\)の増加量は
\(2 \times 4^2- 2 \times 3^2=32-18=14\)
となり不適
すなわち \(4 \lt a \leq 8\)
\(x:3 \rightarrow a\) のとき
\(y\)の増加量は
\(\{2 \times 4^2-2 \times 3^2\}\)
\(+\{16a-32-(16 \times 4-32)\}\)
\(=14+16a-64=16a-50\)
よって
\(16a-50=60 \iff a=\frac{55}{8}\)
(3) (答) \(a=\large \frac{55}{8}\)
大問4
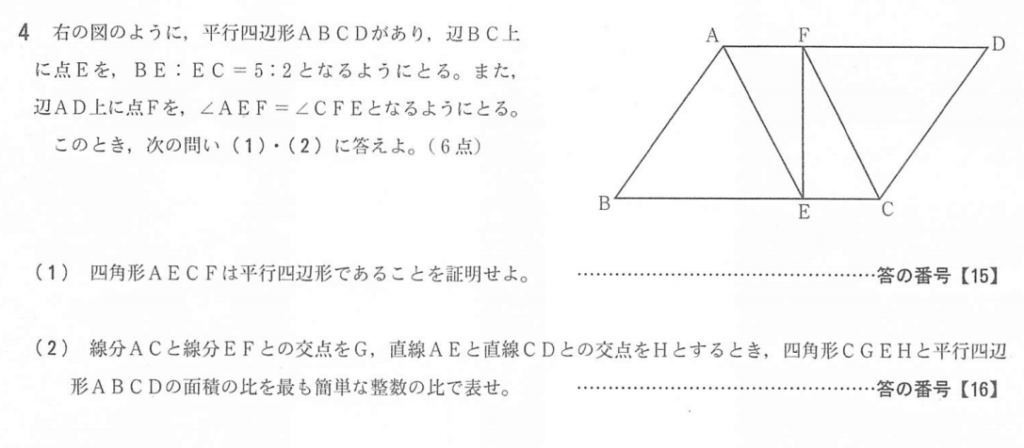
(2)解答例
辺の比や相似比だけで次の順番で計算する。
\(\triangle CGE\)は
平行四辺形\(ABCD \rightarrow \triangle ABC\)
\( \rightarrow AEC \rightarrow \triangle CGE\)
\(\Downarrow\)
平行四辺形\(ABCD \times \frac{1}{2} \times \frac{2}{7} \times \frac{1}{2}\)
\(=\)平行四辺形\(ABCD \times \frac{1}{14}=\triangle CGE\)
\(\triangle EHC\)は
平行四辺形\(ABCD \rightarrow \triangle ABC\)
\( \rightarrow ABE \rightarrow \triangle EHC\)
\(\Downarrow\)
平行四辺形\(ABCD \times \frac{1}{2} \times \frac{5}{7} \times (\frac{2}{5})^2\)
\(=\)平行四辺形\(ABCD \times \frac{2}{35}=\triangle EHC\)
ゆえに
四角形\(CGEH =\triangle CGE +\triangle EHC\)
\(=\)平行四辺形\(ABCD \times \frac{1}{14}\)
\(+\)平行四辺形\(ABCD \times \frac{2}{35}\)
\(=\)平行四辺形\(ABCD \times \frac{9}{70}\)
(2) (答) \(9:70\)
【別解】
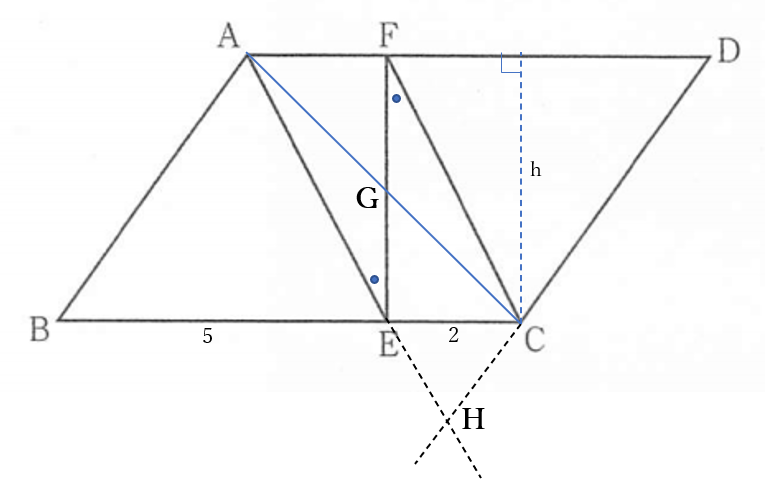
右の図のように
平行四辺形\(ABCD\)の高さを\(h\)とする。
また、\(BE:BC=5:2\) より
\(BE=5,\quad EC=2\) とする。
\(G\)は、平行四辺形\(AECF\)の対角線の中点だから、
\(\triangle CGE\)の底辺を\(EC\)としたときの
高さは\(\frac{1}{2}h\)である。
よって、\(\triangle CGE\)の面積は
\(2\times \frac{1}{2}h \times \frac{1}{2}=\frac{1}{2}h\)
また、\(\triangle DFC \sim \triangle CEH\)
\(DF=5,\quad CE=2\)
だから
\(\triangle CEH\)の高さは
\(\frac{2}{5}h\)
よって、\(\triangle CEH\)の面積は
\(2\times \frac{2}{5}h \times \frac{1}{2}=\frac{2}{5}h\)
ゆえに四角形\(CGEH\)の面積は
\(\triangle CGE + \triangle CEH\)
\(=\frac{1}{2}h+\frac{2}{5}h=\frac{9}{10}h\)
平行四辺形\(ABCD\)の面積は
\(7h\)
ゆえに四角形\(CGEH\)と平行四辺形\(ABCD\)の面積の比は
\(\frac{9}{10}h:7h=9:70\)
(2) (答) \(9:70\)
大問5
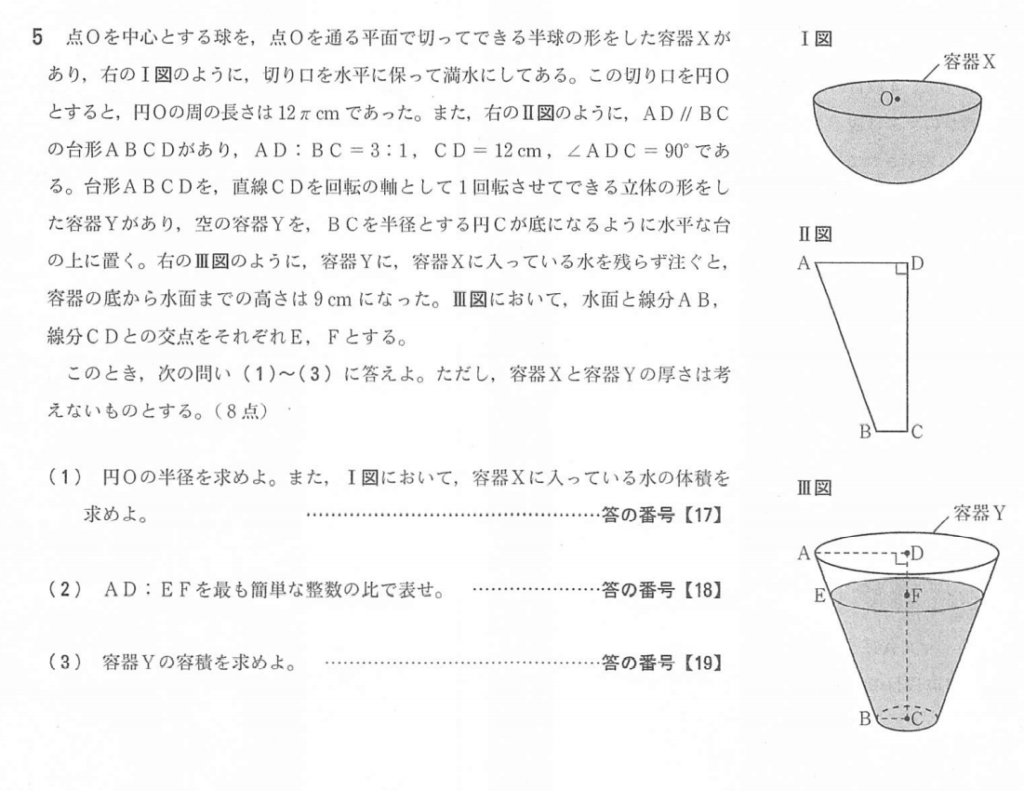
(2)解答例
右下の図のように、
直線\(AB\)と直線\(DC\)との交点を\(G\) とする。
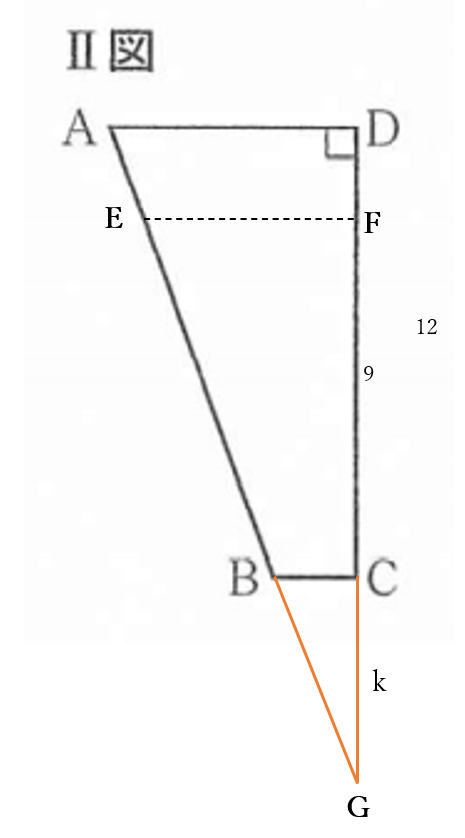
\(CG=k\) とおくと、
\(AD:BC=3:1\) より
\(DG:CG=(12+k):k\)
\(=3:1\)
\(\iff 3k=12+k\)
\(\iff k=6\)
よって
\(AD:EF=DG:FG\)
\(=(12+6):(9+6)=6:5\)
(2)(答) \(AD:EF=6:5\)
(3)解答例
直角三角形\(EFG\)を直線\(CD\)を回転の軸として1回転してできる円錐の体積と容器\(Y\)に入れられた水の体積から\(EF\)を求める。
\(EF=r\)とおくと円錐\(EFG\)の体積は
\(FG=15\)より
\(15\pi r^2 \times \frac{1}{3}=5\pi r^2\)
\(EF=r\)としたときの水の体積は、
\(\triangle EFG\)と\(\triangle BCG\)の相似比
\(15:6=5:2\)から
\(5\pi r^2 \times \{1-(\frac{2}{5})^3\}\)
\(=5\pi r^2 \times \frac{117}{125}=\frac{117}{25}\pi r^2\)
(1)より
\(\frac{117}{25}\pi r^2=144\pi\)
\(\iff r^2=\frac{25\times 144}{117}\)
\(\iff r=\frac{5\times 12}{3\sqrt{13}}\)
\(=\frac{20}{\sqrt{13}}\)
よって(2)より
\(AD=\frac{6}{5}r=\frac{24}{\sqrt{13}}\)
ゆえに求める容器\(Y\)の容積は
\(DG:CG=18:6=3:1\)より
\(\pi (\frac{24}{\sqrt{13}})^2\times 18 \times \frac{1}{3} \times \{1-(\frac{1}{3})^3\}\)
\(=\frac{24^2}{13}\times 6\times \frac{26}{27}\pi\)
\(=256\pi\)
(3) (答) \(256 \Large \pi\) \((cm^3)\)
大問6

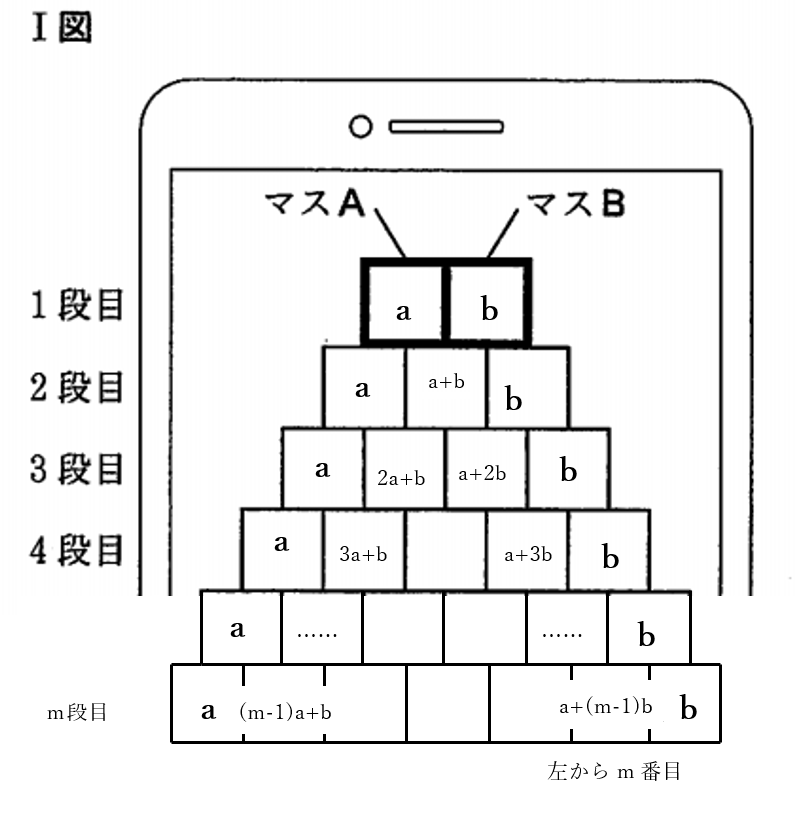
(3)解答例
右下の図のように
マス \(A\) に \(a\)
マス \(B\) に \(b\)
を入力すると
\(m\)段目の
左から2番目のマスには
\((m-1)a+b\)
左から\(m\)番目のマスには
\(a+(m-1)b\)
が表示される。
したがって題意より
\(a=22, \ b=-2\) のとき
\(\{22+(m-1)(-2)\}^2=(2m-1)22+(-2)\)
\(\iff 4m^2-96m+24^2=44m-24\)
\(\iff m^2-35m+150=0\)
\(\iff (m-5)(m-30)=0\)
\(\iff m=5, \ 30\)
(3) (答) \(m=5, \ 30\)