解答に時間を要する問題が2題出題されている。大問3(2)② と、 大問4(2)である。時間を要するとは、計算にではなく、問題の理解や解法そのものにである。とくに、大問4(2)はてごわい。
50分という限られた時間の中でこの2題を解くことのできた受験生はいったいどれくらい居たのだろうか?
大問3(2)②の考察
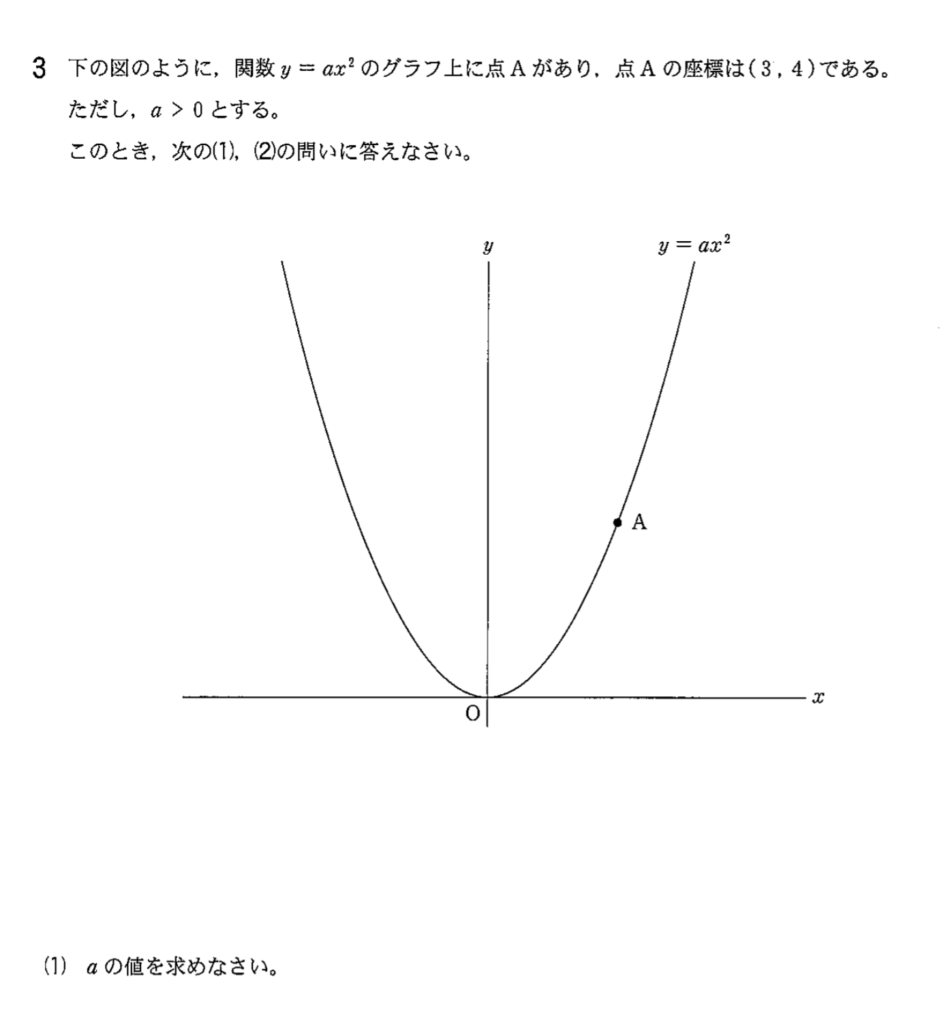

(2)②
①までに分かっていること
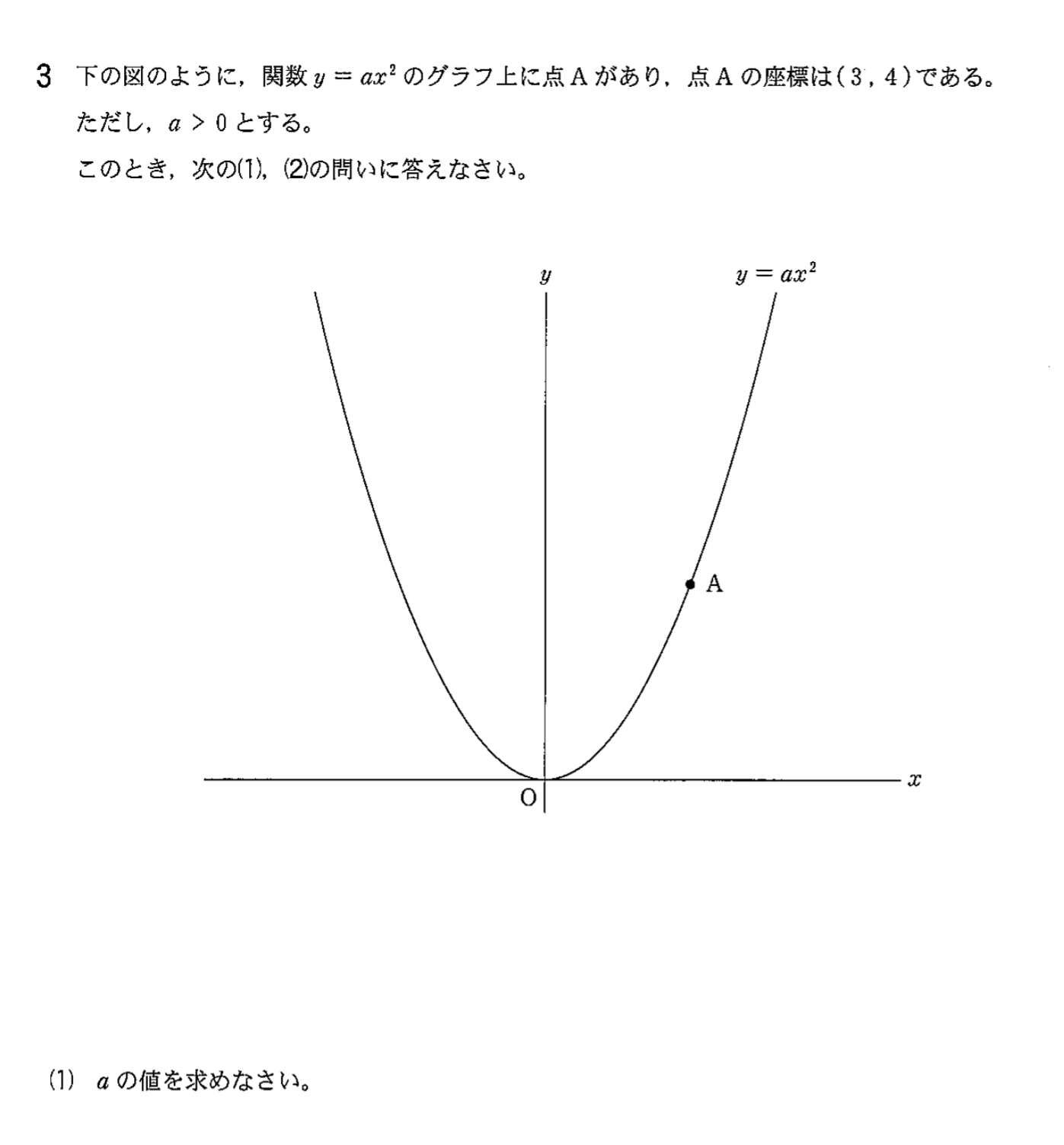
点A(3,4)、 放物線の方程式 \(y=\frac{4}{9}x^2\)
直線ABの方程式 \(y=\frac{1}{2}x+\frac{5}{2}\)
したがって、直線\(l\)の方程式は
\(y=\frac{1}{2}x\) 点Cの座標は\((3,\frac{3}{2})\)
直線OAの方程式は
\(y=\frac{4}{3}x\) 点Dの\(x\)座標を\(k\)とおくと
\(k>3\) 、 \(D(k,\frac{4}{9}k^2)\)、 \(E(k,\frac{4}{3}k)\) 、 \(F(k,\frac{1}{2}k)\)
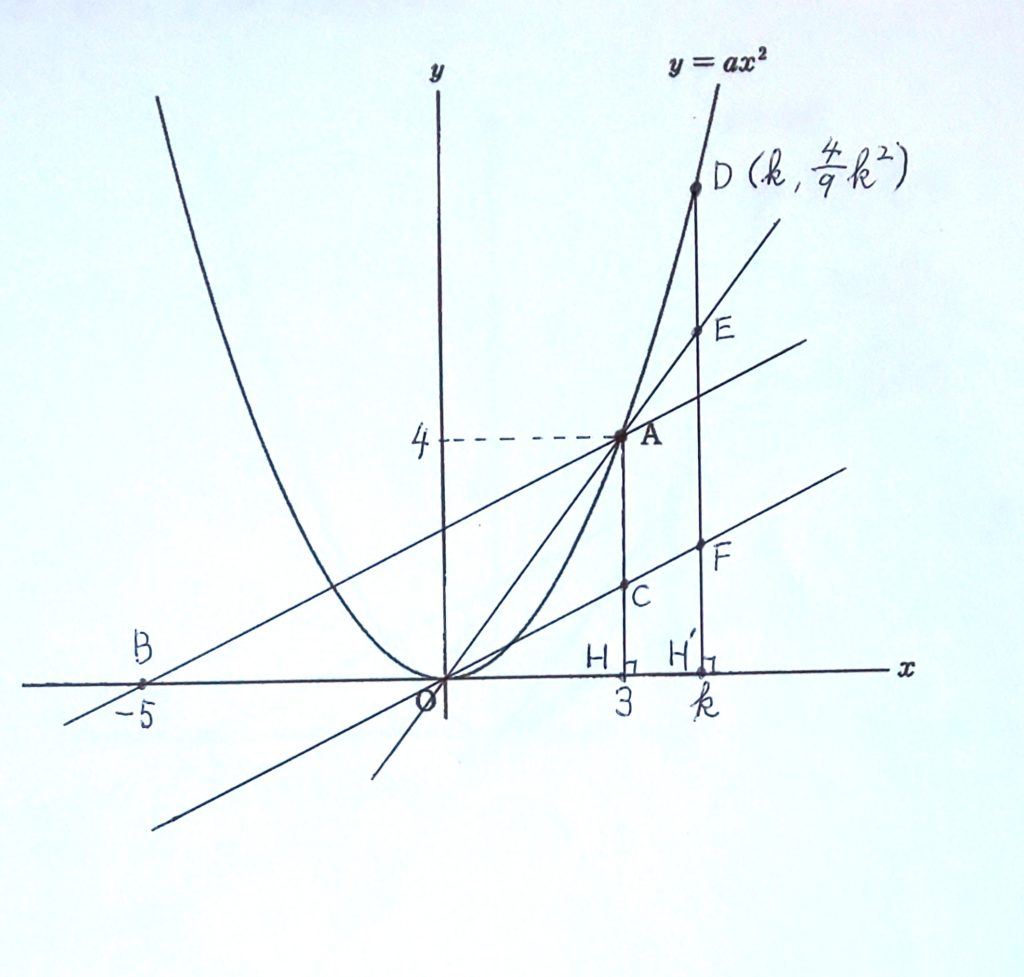
ここで、点Aからx軸に下した垂線の足をH、点Dからx軸に下した垂線の足をH’とする。
\(\triangle AOC\) の面積と
四角形\(ACFE\)の面積の比が
16:9であるから、
\(\triangle AOC\)と\(\triangle EOF\)に着目して
\(\triangle AOC \sim \triangle EOF\)ゆえ
\(\triangle AOC\) の面積と\(\triangle EOF\)の面積の比は\(16:(16+9)=16:25\)
面積比は相似比の2乗に比例するから
\(OA:OE=OH:OH’=4:5\)
\(\iff 3:k=4:5 \iff k=\frac{15}{4}\)
よって、求める点Dの座標は
\(D(\frac{15}{4},\frac{25}{4})\)
(2)②(答) \(D(\frac{15}{4},\frac{25}{4})\)
解法のポイントとしては、
・問題文を読んで作図する
・\(\triangle AOC\) の面積と四角形\(ACFE\)の面積の比が16:9ということから、\(\triangle AOC\) の面積と\(\triangle EOF\)の面積の比に持っていく
の2点である。
大問4(2)の考察

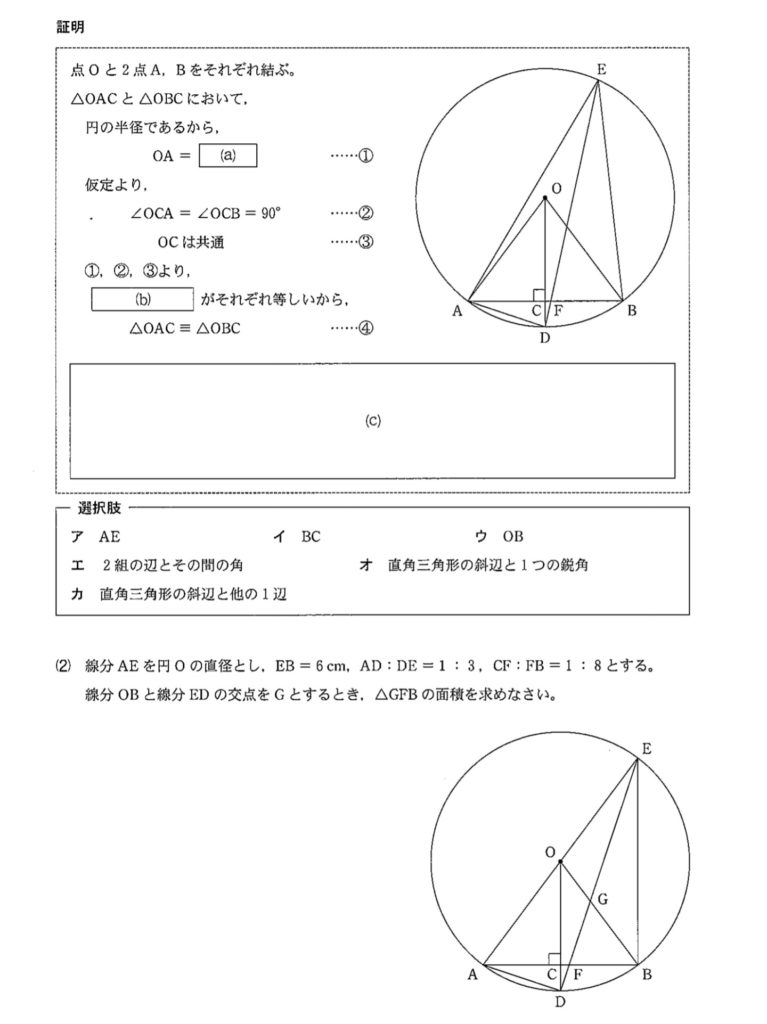
大問4 解答例1
全問より \(\triangle EAD \sim \triangle EFB\) 、\(OC \perp AB\)
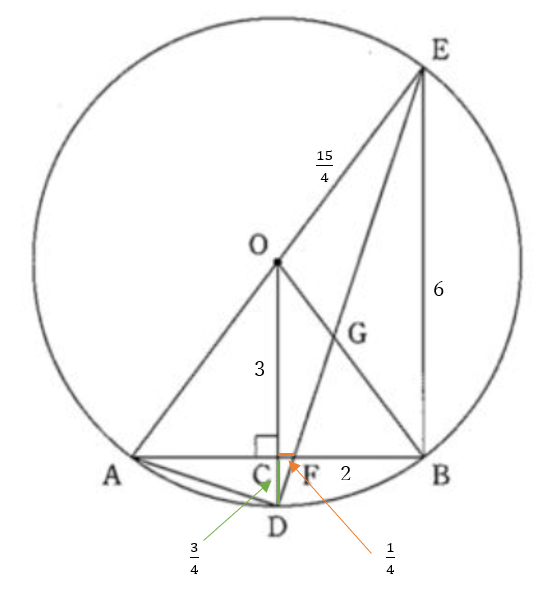
線分\(AE\)は円\(O\)の直径だから
\(\angle EBA =90^{\circ}\)
\(AD:DE=1:3, EB=6\) より
\(FB=2\) また、\(OC=3\)
\(CF:GB=1:8\cdots\)① だから
\(CF:2=1:8 \iff CF=\frac{1}{4}\)
よって \(CB=\frac{1}{4}+2=\frac{9}{4}\)
\(\triangle OCB\) の面積は
\(\triangle OCB=3\times \frac{9}{4} \times \frac{1}{2}\)
\(=\frac{27}{8}\cdots\)②
\(\triangle EBF \sim \triangle DCF\)だから
\(\iff CF:CD=1:3\)
\(\iff CD=\frac{3}{4}\)
\(\iff OD=3+\frac{3}{4}\)
\(=\frac{15}{4}=EO\)
\(\triangle EAD \sim \triangle EFB\)だから
\(\angle OEG=\angle BEG\) よって
\(EO:EB=OG:GB=\frac{15}{4}:6\)
\(=5:8\cdots\)③
①②③より
\(\triangle GFB=\triangle OCB \times \frac{8}{9} \times \frac{8}{13}\)
\(=\frac{27}{8}\times \frac{8}{9} \times \frac{8}{13}\)
\(=\frac{24}{13}\)
大問4(2) (答) \(\large \frac{24}{13}\) \((cm^2)\)
大問4 解答例2
線分\(AE\)は円\(O\)の直径だから\(\angle EBA =90^{\circ}\)
\(AD:DE=1:3, EB=6\) より \(FB=2\) ,\(CF:GB=1:8\) だから \(CF:2=1:8 \iff CF=\frac{1}{4}\)
よって\(CB=\frac{1}{4}+2=\frac{9}{4}\)
\(\triangle OAB\) は \(AC=CB\) の二等辺三角形だから \(AB=2CB=2 \times \frac{9}{4}=\frac{9}{2}\)
よって \(AE=\sqrt{AB^2+EB^2}=\sqrt{(\frac{9}{2})^2+6^2}\)
\(=\sqrt{\frac{81+4 \times 36}{4}}=\sqrt{\frac{225}{4}}=\frac{15}{2}\)
ゆえに \(OA=OD=\frac{15}{4}\)
ここで \(OD/\!/EB\) だから \(\triangle ODG \sim \triangle BEG\)
よって \(OG:BG=OD:BE\)
\(=\frac{15}{4}:6=5:8\)・・・(*)
\(\triangle OBE\)の面積は \(\frac{1}{2} \times BE \times CB=\frac{1}{2} \times 6 \times \frac{9}{4}=\frac{27}{4}\)
だから \(\triangle BEG\)の面積は(*)より
\(\triangle OBE \times \frac{8}{5+8}=\frac{27}{4} \times \frac{8}{13}=\frac{54}{13}\)
ゆえに求める \(\triangle GFB\) の面積は
\(\triangle GFB=\triangle EFB – \triangle BEG \)
\(=6-\frac{54}{13}=\frac{6 \times 13-54}{13}=\frac{78-54}{13}=\frac{24}{13}\)
大問4(2) (答) \(\large \frac{24}{13}\) \((cm^2)\)
【解放のポイント】
限られた時間の中で、答えを導き出すのはかなり困難と思える。
\(OG:BG=5:8\) を求めることができるかが解法の鍵である。