では、2次関数の一般形 $$ \Large y=ax^2+bx+c \quad (a\neq 0) $$ のグラフを描いてみましょう。
例題3
次の2次関数の頂点と軸を求め、グラフをかきなさい。
(1) \(\Large y=x^2-6x+5\)
(2) \(\Large y=x^2+3x+1\)
(3) \(\Large y=-x^2+4x-4\)
(4) \(\Large y=-2x^2-4x+5\)
(5) \(\Large y=\frac{1}{2}x^2-2x+4\)
解答
(1) \(\Large y=x^2-6x+5\)
\(y=a(x-p)^2+q\) の形に式変形します。
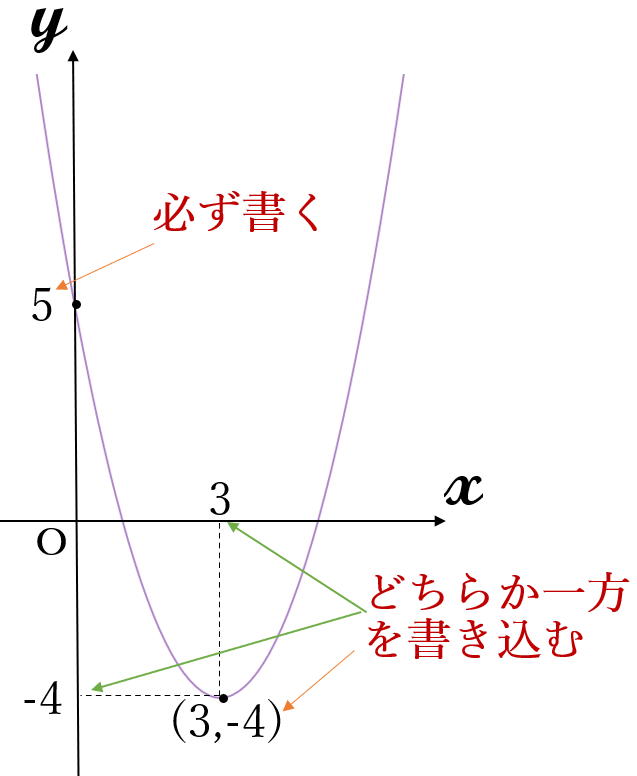
\(y=(x-3)^2-4\)
頂点\((3, \ -4)\)
軸 \(x=3\)
下に凸
《注意》:\(x \ \)軸との交点を書き込むかは、学校の先生の指示に従ってください。2次方程式を解く必要があります。2次方程式については、後でやります。
解答
(2) \(\Large y=x^2+3x+1\)
\(y=a(x-p)^2+q\) の形に式変形します。
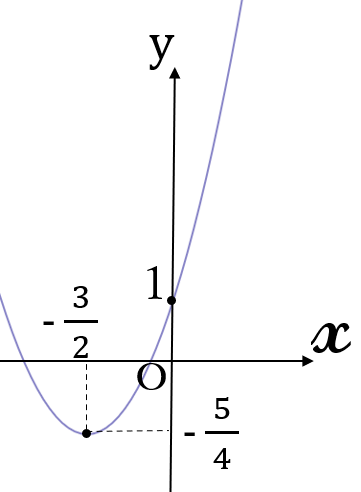
\(y=\large (x+ \frac{3}{2})^2-\frac{5}{4}\)
頂点\(\large (-\frac{3}{2}, \ -\frac{5}{4})\)
軸 \(x=\)\(\large -\frac{3}{2}\)
下に凸
解答
(3) \(\Large y=-x^2+4x-4\)
\(y=a(x-p)^2+q\) の形に式変形します。
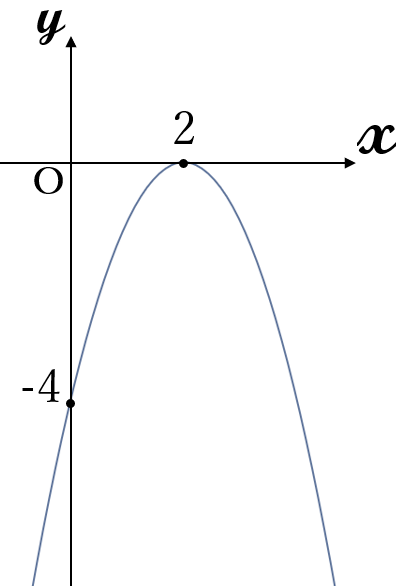
\(y=-(x-2)^2\)
頂点\((2, \ -4)\)
軸 \(x=2\)
上に凸
解答
(4) \(\Large y=-2x^2-4x+5\)
\(y=a(x-p)^2+q\) の形に式変形します。
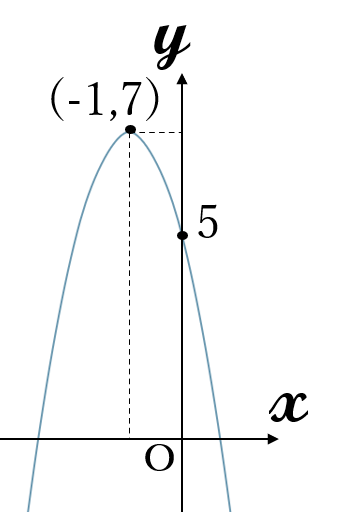
\(y=-2(x+1)^2+7\)
頂点\((-1, \ 7)\)
軸 \(x=-1\)
上に凸
解答
(5) \(\Large y=\frac{1}{2}x^2-2x+4\)
\(y=a(x-p)^2+q\) の形に式変形します。
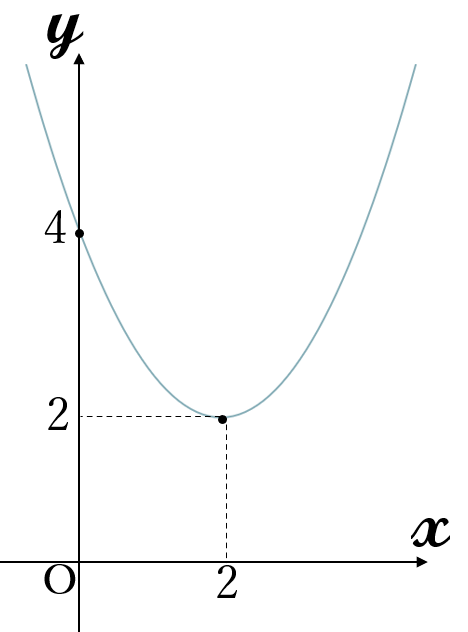
\(y=\)\(\large \frac{1}{2}\)\((x-2)^2+2\)
頂点\((2, \ 2)\)
軸 \(x=2\)
下に凸
練習3
次の2次関数のグラフをかきなさい。また、その軸と頂点を求めなさい。
(1) \(\Large y=x^2-6x+4\)
(2) \(\Large y=2x^2+4x+3\)
(3) \(\Large y=-2x^2+8x-4\)
(4) \(\Large y=2x^2+2x+2\)
(5) \(\Large y=-\frac{1}{2} x^2-3x\)
解答
(1) \(\Large y=x^2-6x+4\)
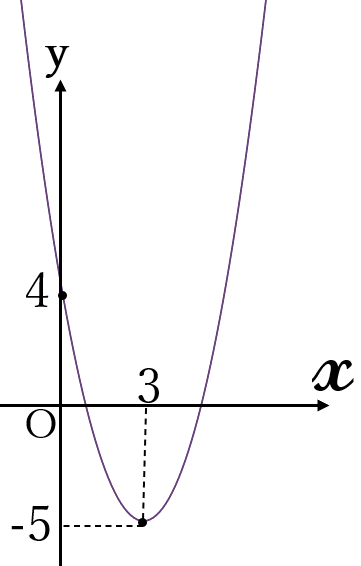
\(y=(x-3)^2-5\)
頂点\( \ (3,-5)\)
軸\( \ x=3\)
(2) \(\Large y=2x^2+4x+3\)
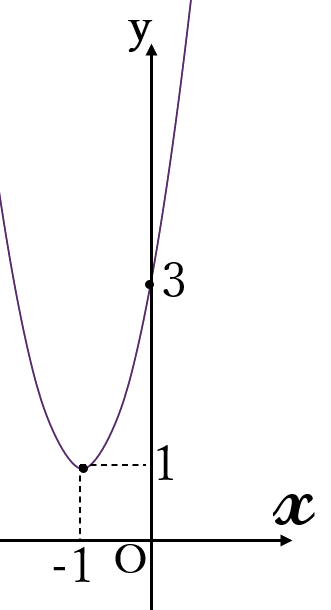
\(y=2(x+1)^2+1\)
頂点\( \ (-1,1)\)
軸\( \ x=-1\)
(3) \(\Large y=-2x^2+8x-4\)
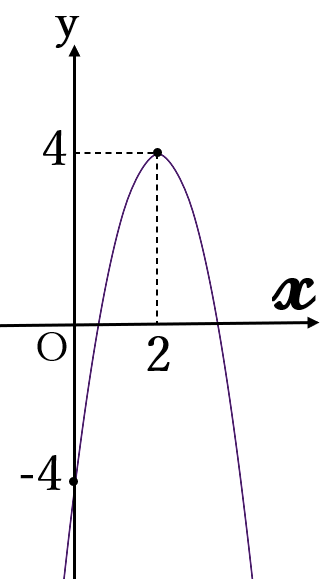
\(y=-2(x-2)^2+4\)
頂点\( \ (2,4)\)
軸\( \ x=2\)
(4) \(\Large y=2x^2+2x+2\)
\(y=2x^2+2x+2=2(x^2+x)+2\)
\(=2\{(x+\frac{1}{2})^2-\frac{1}{4}\}+2\)
\(=2(x+\frac{1}{2})^2-\frac{1}{2}+2\)
\(=2(x+\frac{1}{2})^2+\frac{3}{2}\)
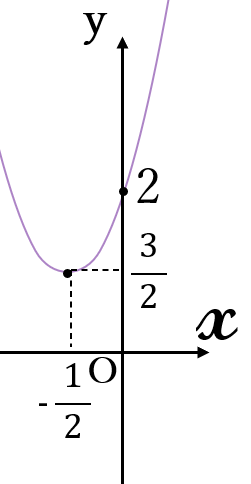
頂点\(\large \ (-\frac{1}{2},\frac{3}{2})\)
軸\(\large \ x=-\frac{1}{2}\)
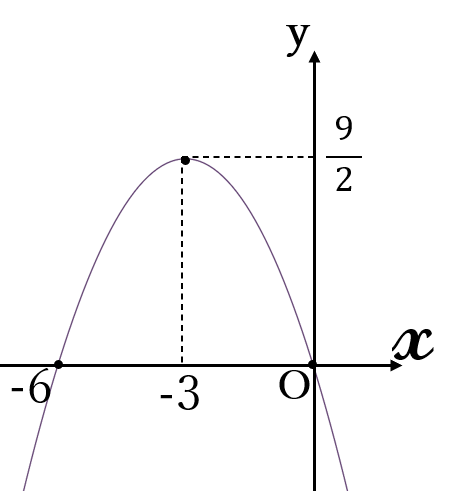
(5) \(\Large y=-\frac{1}{2} x^2-3x\)
\(y=-\frac{1}{2} x^2-3x=-\frac{1}{2}(x^2+6x)\)
\(=-\frac{1}{2}\{(x+3)^2-9\}\)
\(=-\frac{1}{2}(x+3)^2+\frac{9}{2}\)
頂点\( \ (-3, \ \)\(\large \frac{9}{2}\)\()\quad\) 軸\( \ x=-3\)
2次関数の最大値・最小値
第一段階での2次関数のグラフ(放物線)を描くことはできました。いよいよ次は、メインの最大値最小値です。大学入試にもよく出題される分野です。
定義域と値域
関数\( \ y=f(x) \ \)において、\(x \ \)のとりうる値の範囲を、この関数の定義域といいます。また、その定義域にたいして、\(y \ \)のとりうる値の範囲をこの関数の値域といいます。
定義域は、次の例ように、関数の式の後ろに(右に)表示されることが多いです。
例5
\(y=x^2-2x-3\) \((-1 \leq x \leq 5)\)
また、2次関数\( \ y=f(x) \ \)の定義域について特に断りがない場合には、2次関数\( \ y=f(x) \ \)の定義域は、実数\( \ x \ \)の全体になります。
2次関数の値の増加減少と
2次関数のグラフ
2次関数の値(\( \ y \ \)の値)は、放物線の頂点を境にして増加と減少が入れ替わります。
グラフとともに、視覚的に捉えましょう。
\(a \gt 0 \ \)の場合、グラフは下に凸だから
\(x \lt p \ \)のとき、関数の値(\( \ y \ \)の値)は、減少
\(x \gt p \ \)のとき、関数の値(\( \ y \ \)の値)は、増加します。
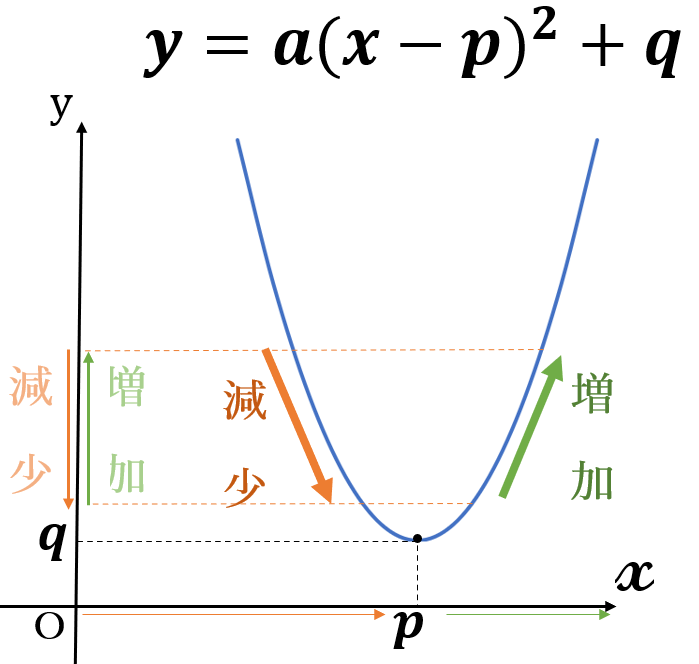
関数の値(\( \ y \ \)の値)は、上(\(y\)軸の矢印の方向)に行くほど大きくなり、下に行くほど小さくなります。
\(a \lt 0 \ \)の場合、グラフは上に凸だから
\(x \lt p \ \)のとき、関数の値(\( \ y \ \)の値)は、増加
\(x \gt p \ \)のとき、関数の値(\( \ y \ \)の値)は、減少します。
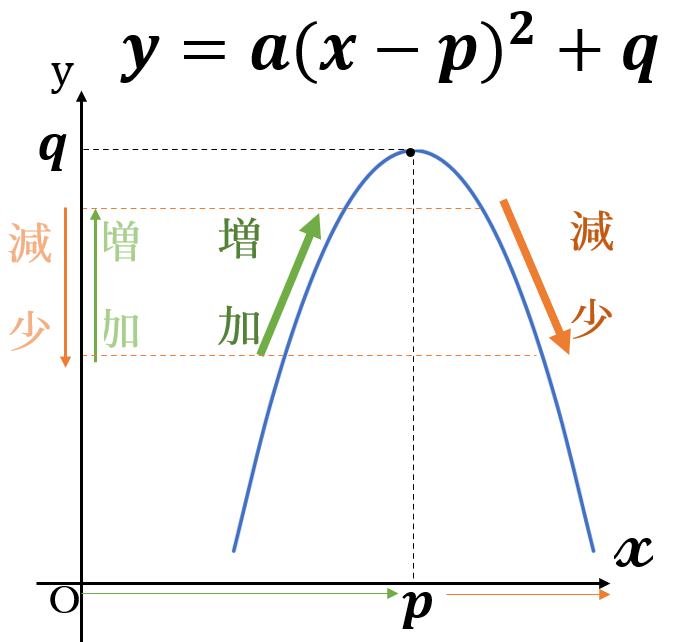
関数の値(\( \ y \ \)の値)は、上(\(y\)軸の矢印の方向)に行くほど大きくなり、下に行くほど小さくなります。
2次関数の増加減少と
最大値最小値 その1
定義域がすべての実数であるとき
関数の増加減少が放物線の頂点で入れ替わることから、頂点の\( \ y \ \)座標が2次関数の最大値または最小値になります。
\(a \gt 0 \ \)で、定義域がすべての実数のとき、
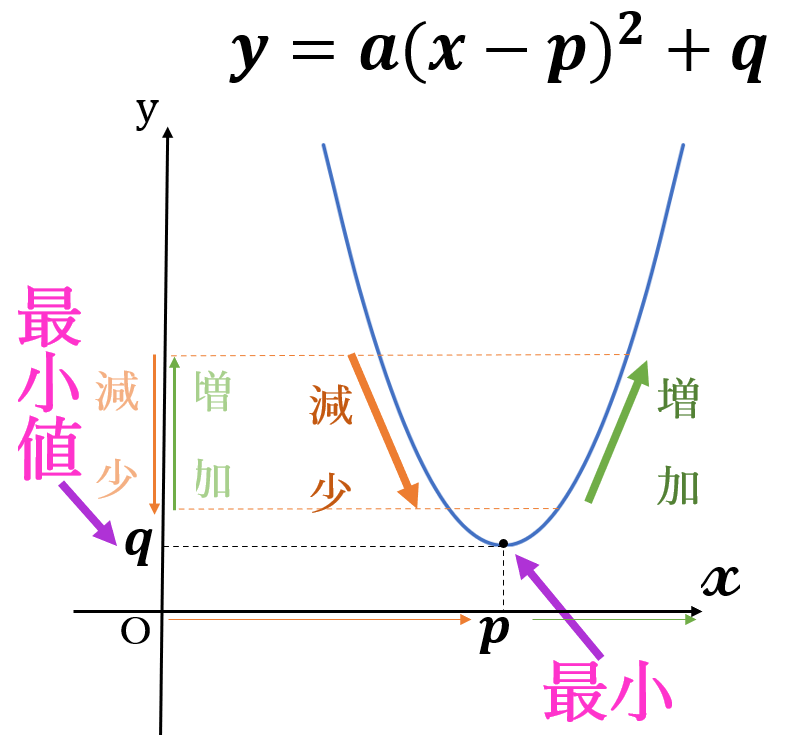
「言い方(書き方)」は次のようになります。
「この関数は、\(x=p \ \)のとき、最小となり、最小値は\( \ q \ \)である。最大値はない。」
このことをつぎのように書きます。
最小値\( \ q \ \) \((x=p)\)、 最大値はない
\(\large \Uparrow \ \)この書き方を覚えると、テストのとき楽です。
\(a \lt 0 \ \)で、定義域がすべての実数のとき、
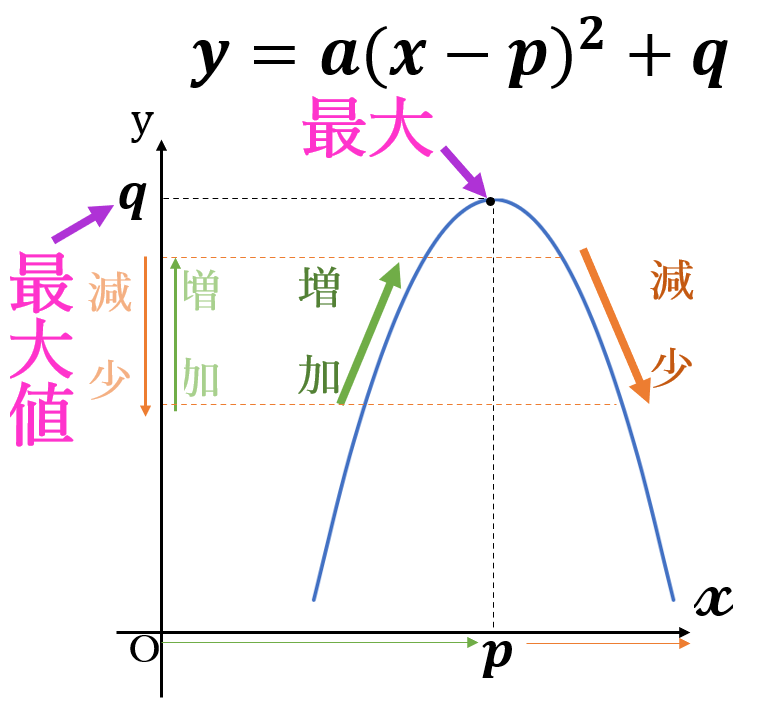
「言い方(書き方)」は次のようになります。
「この関数は、\(x=p \ \)のとき、最大となり、最大値は\( \ q \ \)である。最小値はない。」
このことをつぎのように書きます。
最大値\( \ q \ \) \((x=p)\)、 最小値はない
注意
定義域に指定がない場合には
定義域は
「すべての実数」
ということになります。
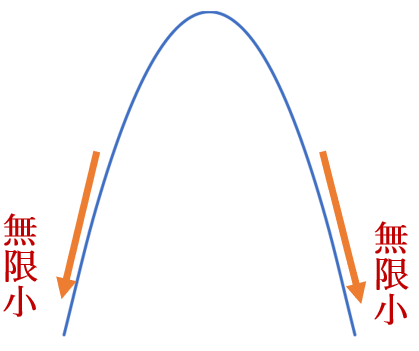
最大最小が
無限大無限小になるとき、
値としては定まらないので
「最大値はない」「最小値はない」
となります。
例題4
次の2次関数の最大値、最小値があれば、それを求めなさい。
(1) \(\Large y=2(x-3)^2-1\)
(2) \(\Large y=-x^2+4x+3\)
(3) \(\Large y=2x^2+4x+3\)
(4) \(\Large y=-x^2-4x-1\)
解答
(1) \(\Large y=2(x-3)^2-1\)
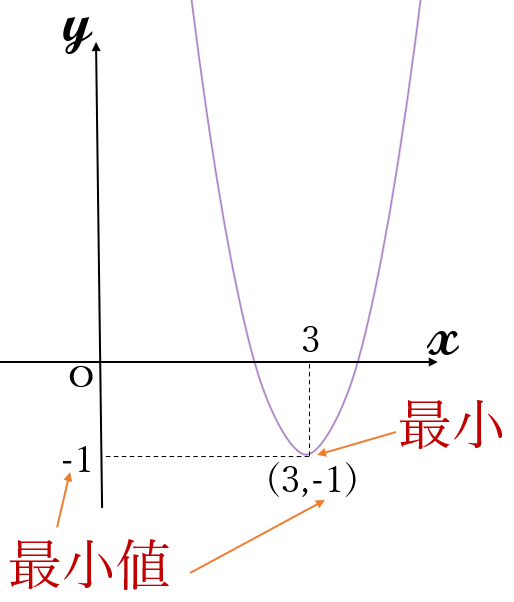
頂点\((3, \ -1)\)
下に凸
最小値\( \ -1 \quad (x=3)\)
最大値はない
\(\Uparrow\)
書き忘れない!
解答にグラフを書く必要はありません。グラフは頭の中でイメージし、答えだけを書けばよいです。「グラフをかきなさい」という指示があれば書きましょう。
解答
(2) \(\Large y=-x^2+4x+3\)
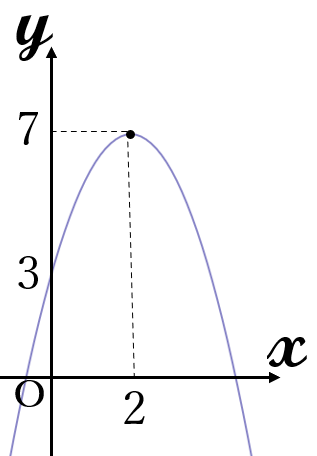
\(y=-x^2+4x+3\)
\(=-(x^2-4x)+3\)
\(=-\{(x-2)^2-4\}+3\)
\(=-(x-2)^2+4+3\)
\(\Large =-(x-2)^2+7\)
頂点\((2, \ 7)\)
上に凸
最大値\( \ 7 \quad (x=2)\)
最小値はない
\(\Uparrow\)
書き忘れない!
解答
(3) \(\Large y=2x^2+4x+3\)
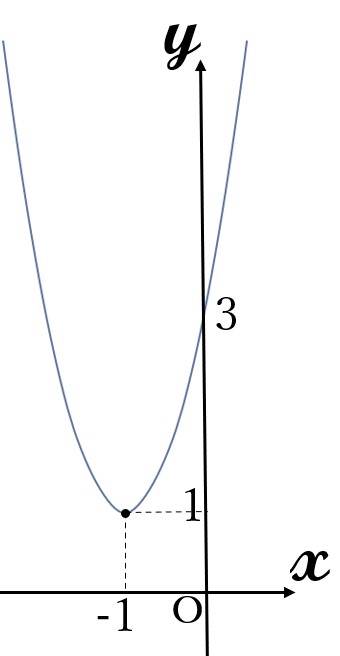
\(y=2x^2+4x+3\)
\(=2(x^2+2x)+3\)
\(=2\{(x+1)^2-1\}+3\)
\(=2(x+1)^2-2+3\)
\(\Large =2(x+1)^2+1\)
頂点\((-1, \ 1)\)
下に凸
最小値\( \ 1 \quad (x=-1)\)
最大値はない
\(\Uparrow\)
書き忘れない!
解答
(4) \(\Large y=-x^2-4x-1\)
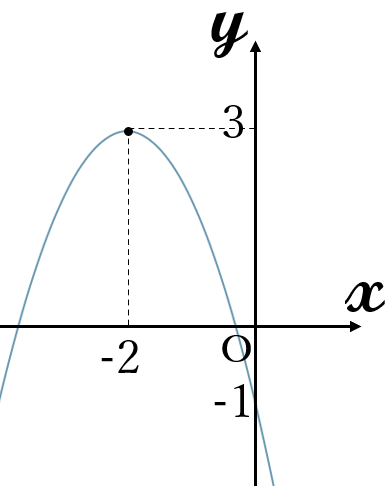
\(y=-x^2-4x-1\)
\(=-(x^2+4x)-1\)
\(=-\{(x+2)^2-4\}-1\)
\(=-(x+2)^2+4-1\)
\(\Large =-(x+2)^2+3\)
頂点\((-2, \ 3)\)
上に凸
最大値\( \ 3 \quad (x=-2)\)
最小値はない
\(\Uparrow\)
書き忘れない!
練習4
次の2次関数の最大値、最小値があれば、それを求めなさい。
(1) \(\Large y=x^2+4x+2\)
(2) \(\Large y=-x^2+6x-4\)
(3) \(\Large y=2x^2+4x+3\)
(4) \(\Large y=-2x^2-6x\)
解答
下に凸なら最小値が、上に凸なら最大値があります。解答用紙に、グラフを書く必要はありません。グラフを頭の中でイメージして、答えを出しましょう。
(1) \(\Large y=x^2+4x+2\)
\(y=x^2+4x+2=(x+2)^2-2\)

頂点\( \ (-2, \ 2)\) 下に凸
最小値 \(2\) \((x=-2)\)
最大値はない
\(\Uparrow\)
書き忘れない!
解答
(2) \(\Large y=-x^2+6x-4\)
\(y=-(x^2-6x)-4\)
\(=-\{(x-3)^2-9\}-4\)
\(=-(x-3)^2+9-4\)
\(=-(x-3)^2+5\)
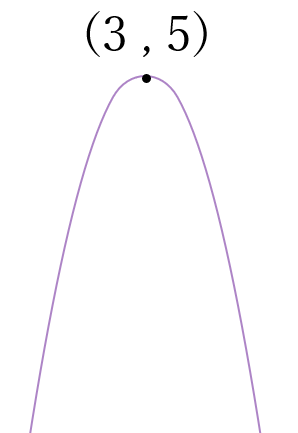
頂点\( \ (3, \ 5)\) 上に凸
最大値 \(5\) \((x=3)\)
最小値はない
\(\Uparrow\)
書き忘れない!
解答
(3) \(\Large y=2x^2+4x+3\)
\(y=2x^2+4x+3=2(x^2+2x)+3\)
\(=2\{(x+1)^2-1\}+3\)
\(=2(x+1)^2-2+3=2(x+1)^2+1\)

頂点\( \ (-1, \ 1)\) 下に凸
最小値 \(1\) \((x=-1)\)
最大値はない
\(\Uparrow\)
書き忘れない!
解答
(4) \(\Large y=-2x^2-6x\)
\(y=-2(x^2+3x)=-2\{(x+\frac{3}{2})^2-\frac{9}{4}\}\)
\(=-2(x+\frac{3}{2})^2+\frac{9}{2}\)
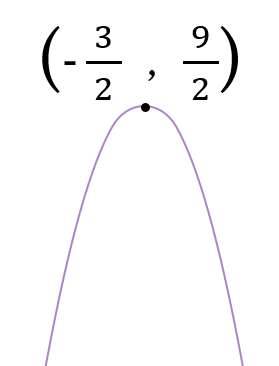
頂点\(\large \ (-\frac{3}{2} \ , \ \frac{9}{2})\)
上に凸
最大値 \(\large \frac{9}{2}\) \(\large (x=-\frac{3}{2})\)
最小値はない
\(\Uparrow\)
書き忘れない!
