関数って何 ❓
関数の概念
多くの高校生が、「関数って何?」という疑問を持つようです。簡単に言えば、次のようになります。
\(x \ \)の値を定めると、その\( \ x \ \)の値に対して、\( \ y \ \)の値がただ一つ定まるとき、\( \ y \ \)を\( \ x \ \)の関数と言います。
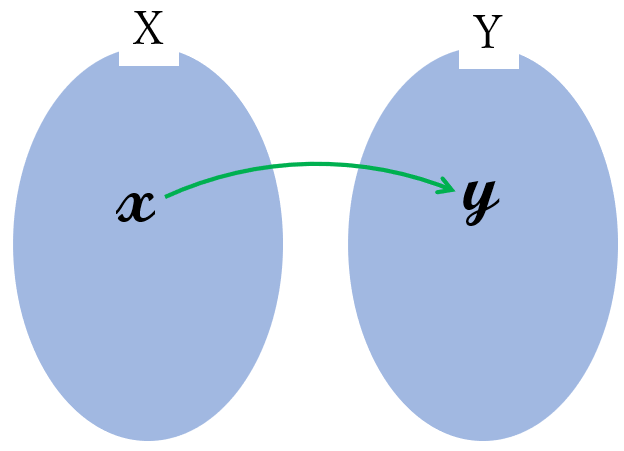
この表現は、少し不正確かもしれませんが、これから2次関数を勉強するのに、この表現で十分と思われます。正確な表現だと、集合と集合の対応でとらえる必要があり、かえって分かりにくくなってしまいます。参考までに、関数の定義をなるべく正確に表現すると、次のようになります。

空でない二つの集合\( \ X \ \)と\( \ Y \ \)の間の対応において、集合\( \ X \ \)のある任意の要素\( \ x \ \)に対して、それに対応する集合\( \ Y \ \)の要素\( \ y \ \)がただ一つ定まるとき、このような対応を、集合\( \ X \ \)から集合\( \ Y \ \)への関数と言います。
関数の表し方
\(y \ \)が\( \ x \ \)の関数であることを、文字\( \ f, \ g \ \)などを用いて、\( \ y=f(x), \ y=g(x) \ \)と表わします。また、この関数を、単に、関数\( \ f(x), \ g(x) \ \)とも表記します。
そして、関数\( \ y=f(x) \ \)において、\(x=a \ \)のときの関数の値(\( \ y \ \)の値)を、\( \ f(a) \ \)で表します。
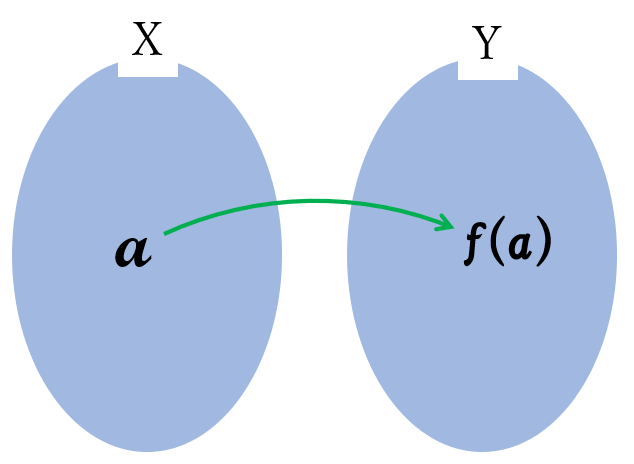
集合を用いると
関数\( \ y=f(x) \ \)
において、
集合\( \ X \ \)の要素\( \ a \ \)に対応して定まる集合\( \ Y \ \)の要素を\( \ f(a) \ \)で表します。
例1
\(\large f(x)=3x-5 のとき、\)
\(\large f(2)=3\times 2-5=1\)
\(\large f(-1)=3\times (-1)-5=-8\)
\(\large \begin{eqnarray} f(a+1) &=& 3\times (a+1)-5 \\ &=& 3a+3-5 \\ &=& 3a-2 \end{eqnarray} \)
練習1
関数\( \ f(x)=-2x+3 \ \)について、次の値を求めなさい。
(1) \(f(0)\) (2) \(f(2)\)
(3) \(f(-1)\) (4) \(f(a-1)\)
解答
(1) $$ \large \begin{eqnarray} f(0) &=& -2 \times 0+3 \\&=& 0+3=3 \end{eqnarray} $$
(2) $$ \large \begin{eqnarray} f(2) &=& -2 \times 2+3 \\ &=& -4+3=-1 \end{eqnarray} $$
(3) $$ \large \begin{eqnarray} f(-1) &=& -2 \times (-1)+3 \\ &=& 2+3=5 \end{eqnarray} $$
(4) $$ \large \begin{eqnarray} f(a-1) &=& -2 \times (a-1)+3 \\ &=& -2a+2+3 \\ &=& -2a+5 \end{eqnarray} $$
中学で勉強した2次関数のグラフ
頂点が原点の放物線
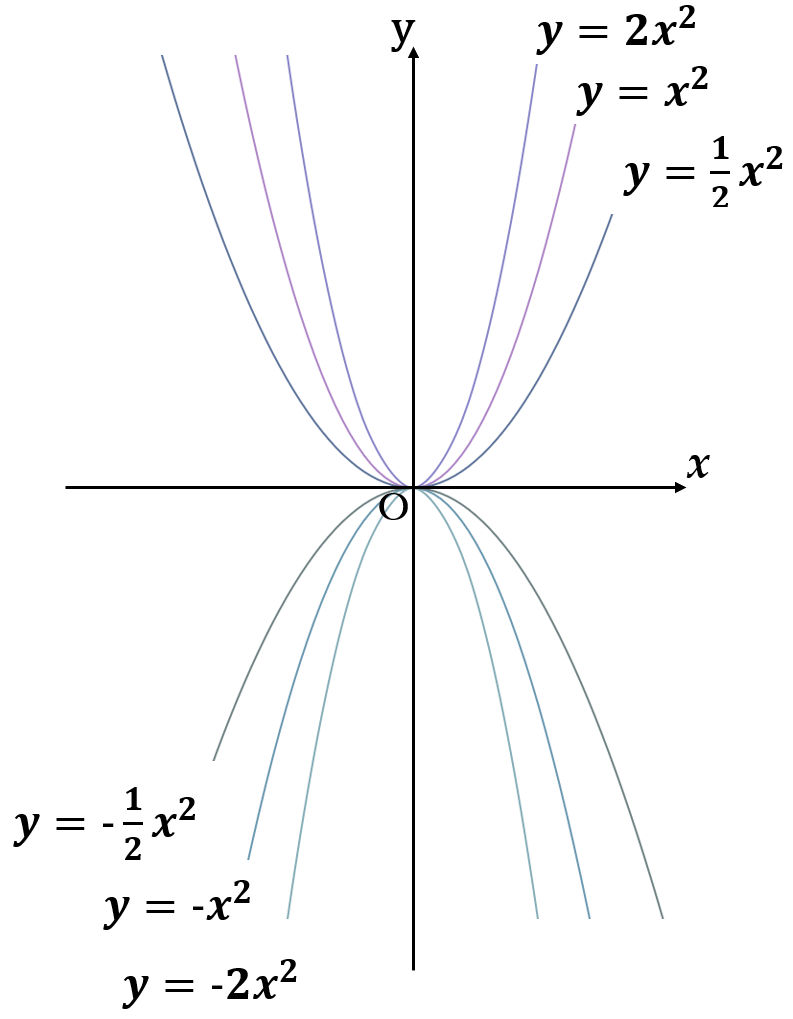
2次関数
\(y=ax^2\)
\((a \neq 0)\)
で表される2次関数を勉強してきました。このグラフは、頂点が原点である放物線で、右の図のようになりました。
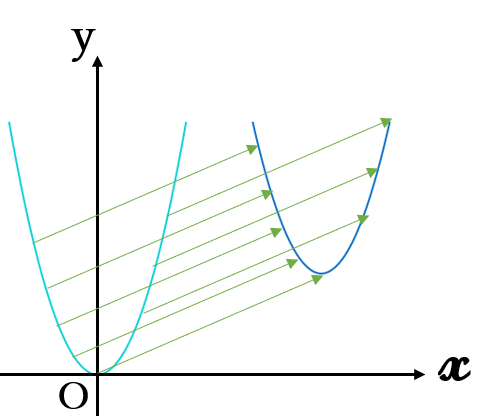
高校では下の図のように頂点が原点から離れた放物線を主に扱います。中学で勉強した2次関数、\(y=ax^2\)は、高校で勉強する2次関数の特別な場合になります。
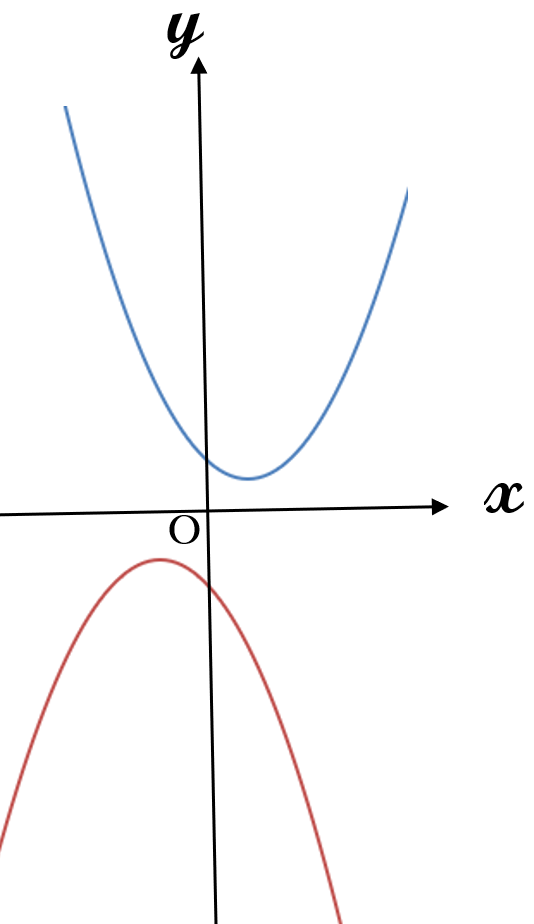
平行移動
頂点が原点ではない放物線は、「頂点が原点である放物線を、移動させたもの」として捉えます。そして、その移動の仕方は
グラフ上のすべての点を、「同じ方向に同じ距離だけ移動」させるものです。
これを「平行移動」と言います。
第一段階として
平行移動した式を求められる。
式の形から、どのような平行移動
かを認識できる。
平方完成することができる。
グラフを描くことができる。
ようにします。
この4つの中で、一番の難敵は
「平方完成」
です
学校の教科書では、この平行移動を次の順番で記述しています。
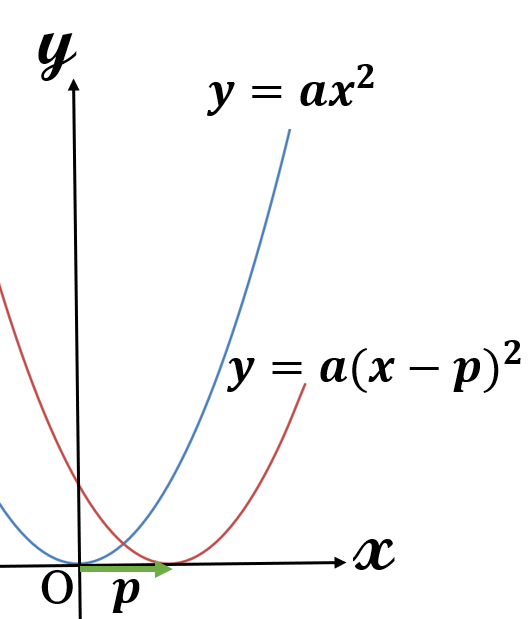
\(x \ \)軸の正の方向に\( \ p \ \)だけ移動
\(y=ax^2 \rightarrow y=a(x-p)^2 \)
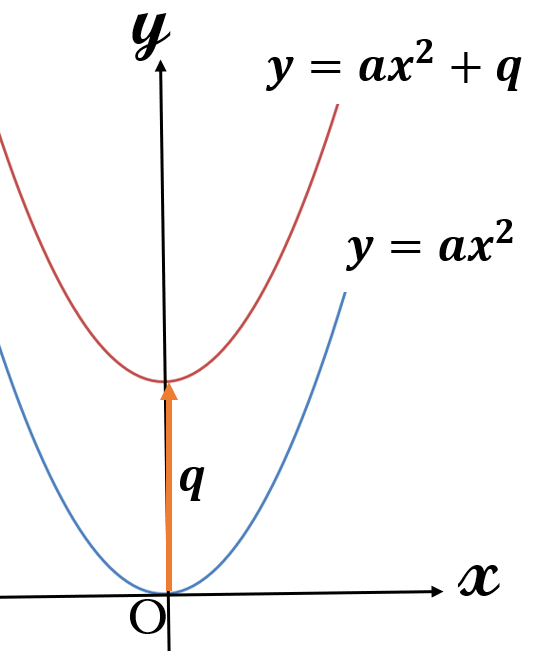
\(y \ \)軸の正の方向に\( \ q \ \)だけ移動
\(y=ax^2 \rightarrow y=ax^2+q\)
\( \Large \Downarrow \)
次ページ
\(x \ \)軸の正の方向に\( \ p \ \)
\(y \ \)軸の正の方向に\( \ q \ \)だけ移動
\(y=ax^2 \rightarrow y=a(x-p)^2+q\)
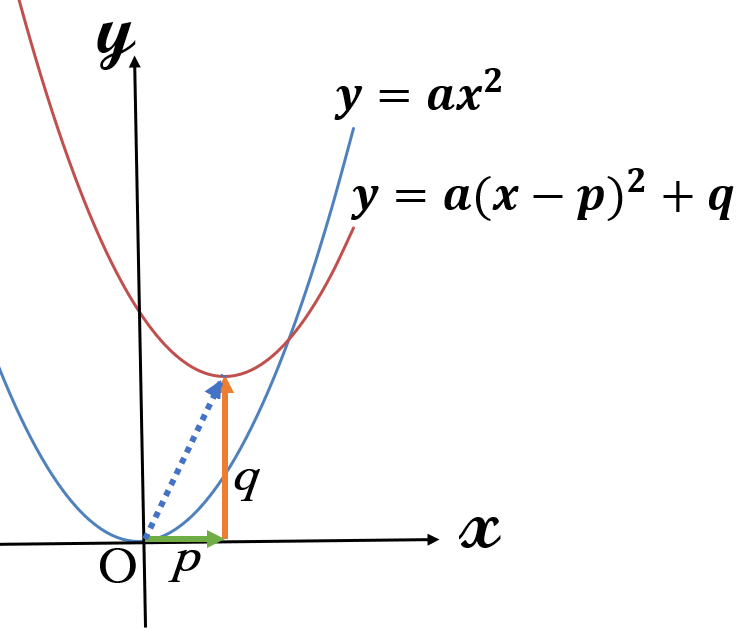
\(y=ax^2 \ \)のグラフを
\(x \ \)軸の正の方向に\( \ p\)
\(y \ \)軸の正の方向に\(q \ \) だけ
平行移動したグラフの方程式は $$ \Large y=a(x-p)^2+q $$
ですが、なぜそうなるのかを理解することは、多くの生徒にとって難しいようです。
具体的な例で平行移動を考察します。
例2
放物線\( \ y=x^2 \ \cdots \ \)①
を\( \ x \ \)軸方向に2,\( \ y \ \)軸方向に1だけ平行移動した放物線の方程式を求めてみましょう。
放物線\( \ y=x^2 \ \cdots \ \)①
放物線①上のある点\( \ P(x,y) \ \)を\( \ x \ \)軸方向に2,\( \ y \ \)軸方向に1だけ平行移動した点を\( \ Q(X,Y) \ \)とおくと、
\(\begin{eqnarray} \left\{ \begin{array}{1} X=x+2 \\ Y=y+1 \end{array} \right. \end{eqnarray} \quad \cdots \ \)②
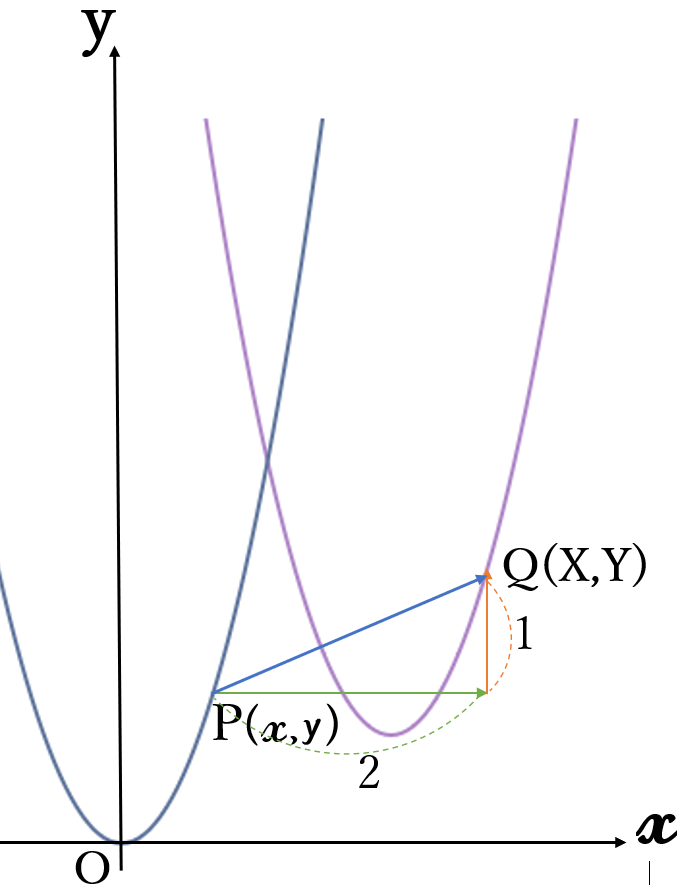
点\( \ P(x,y) \ \)は、\(y=x^2 \ \)上の点だから、\(x \ \)と\( \ y \ \)の間には、\(y=x^2 \ \)という関係が成り立ちます。
②を\( \ x, \ y \ \)について解くと
\(\begin{eqnarray} \left\{ \begin{array}{1} x=X-2 \\ y=Y-1 \end{array} \right. \end{eqnarray} \quad \cdots \ \)③
この\( \ x \ \)と\( \ y \ \)は、①を満たすので、③を①に代入して
\(Y-1=(X-2)^2\)
が得られます。
\(Y-1=(X-2)^2\)

これが点\( \ P(x,y) \ \)を平行移動した点\( \ Q(X,Y) \ \)の満たす方程式です。
\(X \ \)を\( \ x \ \)、\(Y \ \)を\( \ y \ \)に書き換えて、求める放物線の方程式は
\(y=(x-2)^2+1\)
となります。
したがって、放物線\( \ y=x^2 \ \cdots \ \)①
を\( \ x \ \)軸方向に2,\( \ y \ \)軸方向に1だけ平行移動した放物線の方程式は $$ \Large y=(x-2)^2+1 $$ となります。
本書では、2次関数の平行移動を、学校の教科書の順番ではなく、 $$ \large y=a(x-p)^2+q $$ の形からスタートします。 $$ \large y=ax^2, \quad y=a(x-p)^2, \quad y=ax^2+q $$ は、$$ \large y=a(x-p)^2+q $$ の特別な場合として扱います。
このページは、グラフとともに暗記してください。

一般に
\(y=ax^2\)
のグラフを
\(x \ \)軸の正の方向に\( \ p\)
\(y \ \)軸の正の方向に\( \ q \ \)だけ
平行移動したグラフの方程式は $$ \Large y=a(x-p)^2+q $$
です。
\(p\)の前の符号は\(\Large \ – \ \)、\( \ q \ \)の前の符号は\(\Large \ + \ \)です。
練習2
次の(1)~(4)の2次関数のグラフは、$$ \large y=x^2 \quad (a \neq 0) $$ のグラフをどのように平行移動したグラフか答えなさい。
(1) \(\large y=(x-3)^2+1\)
(2) \(\large y=(x+2)^2-3\)
(3) \(\large y=x^2-4\)
(4) \(\large y=(x-1)^2\)
解答
(1) \(\large y=(x-3)^2+1\)
\(x \ \)軸方向に\( \ 3 \ \)、\( \ y \ \)軸方向に\( \ 1 \ \)だけ
平行移動したグラフ
(2) \(\large y=(x+2)^2-3\)
\(x \ \)軸方向に\( \ 3 \ \)、\( \ y \ \)軸方向に\( \ 1 \ \)だけ
平行移動したグラフ
(3) \(\large y=x^2-4\)
\(x \ \)軸方向に\( \ 3 \ \)、\( \ y \ \)軸方向に\( \ 1 \ \)だけ
平行移動したグラフ
(4) \(\large y=(x-1)^2\)
\(x \ \)軸方向に\( \ 3 \ \)、\( \ y \ \)軸方向に\( \ 1 \ \)だけ
平行移動したグラフ
平行移動について理解したところで、2次関数について基本から学習しましょう。
定義域と値域
関数\( \ y=f(x) \ \)において、\(x \ \)のとりうる値の範囲を、この関数の定義域といいます。また、その定義域にたいして、\(y \ \)のとりうる値の範囲をこの関数の値域といいます。
定義域は、次の例ように、関数の式の後ろに(右に)表示されることが多いです。
例3
\(y=x^2-2x-3\) \((-1 ≦ x ≦ 5)\)
また、2次関数\( \ y=f(x) \ \)の定義域について特に断りがない場合には、2次関数\( \ y=f(x) \ \)の定義域は、実数\( \ x \ \)の全体になります。
2次関数のグラフ
\(x \ \)の2次式で表される関数を、\(x \ \)の2次関数といいます。
\(y=f(x) \ \)の\( \ f(x) \ \)が\( \ x \ \)の2次式ならば、\(y=f(x) \ \)は、\(x \ \)の2次関数になります。
2次関数の表し方
2次関数は主に、次の2つの形で表されます。
\(a \neq 0 \ \)で、\(p \ , \ q, \ a, \ b, \ c \ \)を定数として $$ \Large y=a(x-p)^2+q (標準形)$$ $$ \Large y=ax^2+bx+c (一般形) $$
整った形で見た目の良いのが
一般形 \( \Large y=ax^2+bx+c\)
ですが、一般形については、後半で解説します。
2次関数の学習は、
標準形 \( \Large y=a(x-p)^2+q\)
から始めます。
なぜなら、標準形だと、式の形から、平行移動や放物線の頂点が解り、グラフが描きやすいからです。
\(y=a(x-p)^2+q \ \) のグラフ
\(y=a(x-p)^2+q \ \)のグラフは、
\(y=ax^2 \ \)のグラフを
\(x\)軸の正の方向に\(p\)、\(y\)軸の正の方向に\(q\)
だけ平行移動した放物線です。
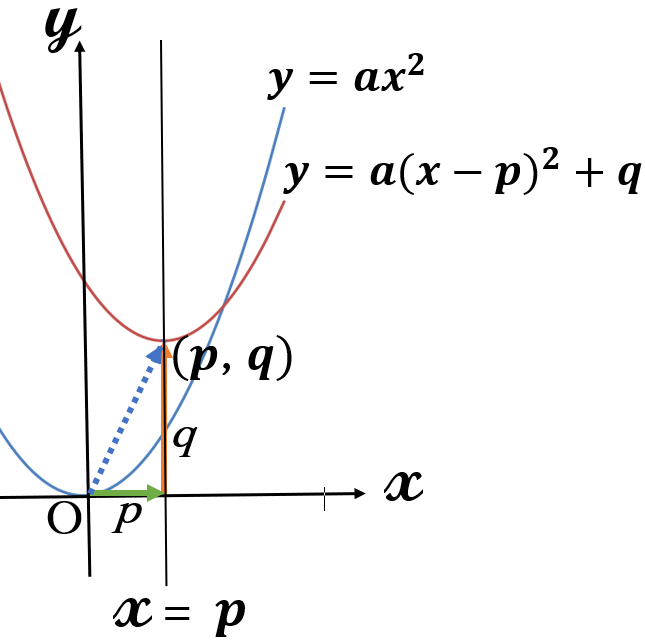
軸は
直線\( \ x=p\)
頂点は
点\( \ (p,q)\)
です。
図と一緒に暗記してください。
しっくりとこない人が多いと思いますが、例2を参考にし、多くの例や例題をよく読み、練習問題を解くことによって、理解が深まっていくと思います。
注意点1
放物線\( \ y=a(x-p)^2+q \ \)は、\(y=ax^2 \ \)を平行移動した放物線ですから
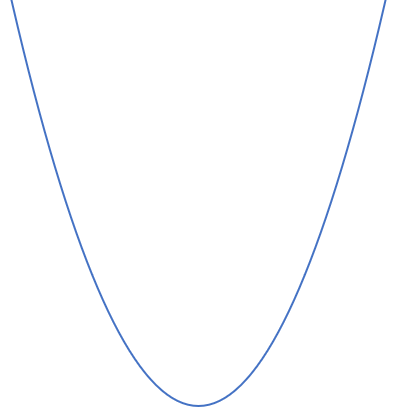
\(a \gt 0 \ \)のとき、下に凸(とつ)
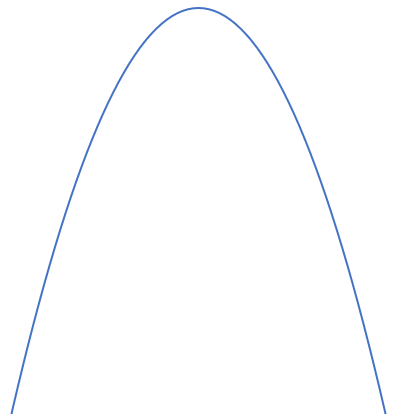
\(a \lt 0 \ \)のとき、上に凸(とつ)
です。
忘れがちですが、 \(\Large a \neq 0\) です。
注意点2
放物線\( \ y=a(x-p)^2+q \ \)の頂点の座標と軸の方程式は、\( \ p, \ q \ \)を求めることによって求まりますが、\( \ p \ \)と\( \ q \ \)の符号に気を付けてください。
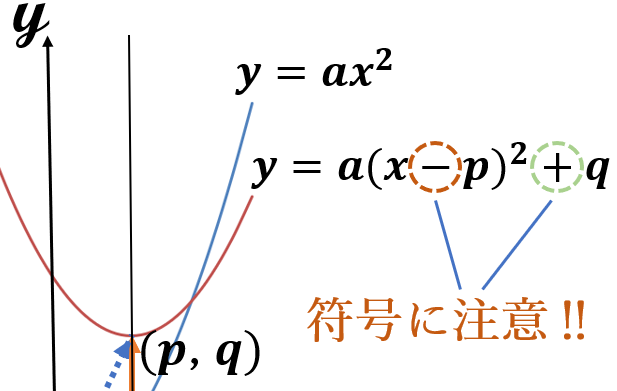
かならず
\( \ p \ \)の前の符号を\( \ \Large – \ \)、\( \ q \ \)の前の符号を\( \ \Large + \ \)にして
\( \ p, \ q \ \)を求めてください。
それでは、例をたくさん紹介しましょう。
例4
(1) \(\large y=(x-1)^2+3\)
\(y=a(x-p)^2+q \ \)の形ですから、
\(p=1, \ q=3 \ \)です。したがって、
\(y=x^2 \ \)のグラフを、\(x \ \)軸方向に\(1\)、\(y \ \)軸方向に\(3 \ \)だけ
平行移動したグラフです。
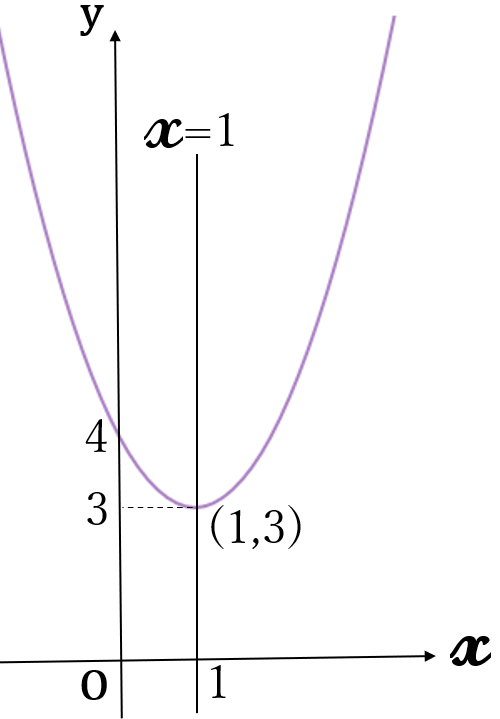
\(a=1 \gt 0 \ \)ですから、
下に凸の放物線です。
軸 \(x=1\)
頂点 \((1, \ 3)\)
(2) \(\large y=(x-1)^2-3\)
\(y=a(x-p)^2+q \ \)の形にします。
\(y=(x-1)^2+(-3) \ \)ですから、
\(p=1, \ q=-3 \ \)です。したがって、
\(y=x^2 \ \)のグラフを、\(x \ \)軸方向に\(1\)、\(y \ \)軸方向に\(-3 \ \)だけ
平行移動したグラフです。
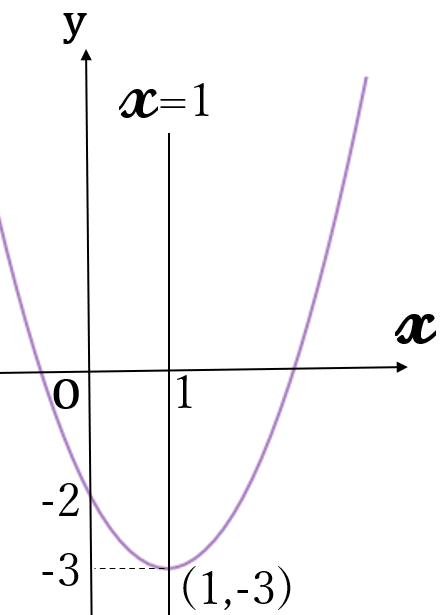
\(a=1 \gt 0 \ \)ですから、
下に凸の放物線です。
軸 \(x=1\)
頂点 \((1, \ -3)\)
(3) \(\large y=(x+1)^2+3\)
\(y=a(x-p)^2+q \ \)の形にします。
\(y=\{x-(-1)\}^2+3 \ \)ですから、
\(p=-1, \ q=3 \ \)です。したがって、
\(y=x^2 \ \)のグラフを、\(x \ \)軸方向に\(-1\)、\(y \ \)軸方向に\(3 \ \)だけ
平行移動したグラフです。
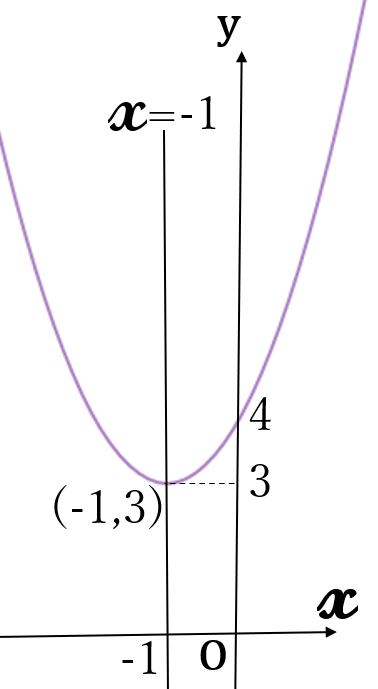
\(a=1 \gt 0 \ \)ですから、
下に凸の放物線です。
軸 \(x=-1\)
頂点 \((-1, \ 3)\)
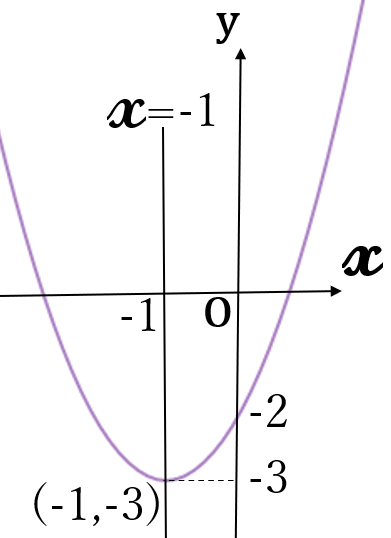
(4) \(\large y=(x+1)^2-3\)
\(y=a(x-p)^2+q \ \)の形にします。
\(y=\{x-(-1)\}^2+(-3) \ \)ですから、
\(p=-1, \ q=-3 \ \)です。したがって、
\(y=x^2 \ \)のグラフを、\(x \ \)軸方向に\(-1\)、\(y \ \)軸方向に\(-3 \ \)だけ
平行移動したグラフです。
\(a=1 \gt 0 \ \)ですから、
下に凸の放物線です。
軸 \(x=-1\)
頂点 \((-1, \ -3)\)
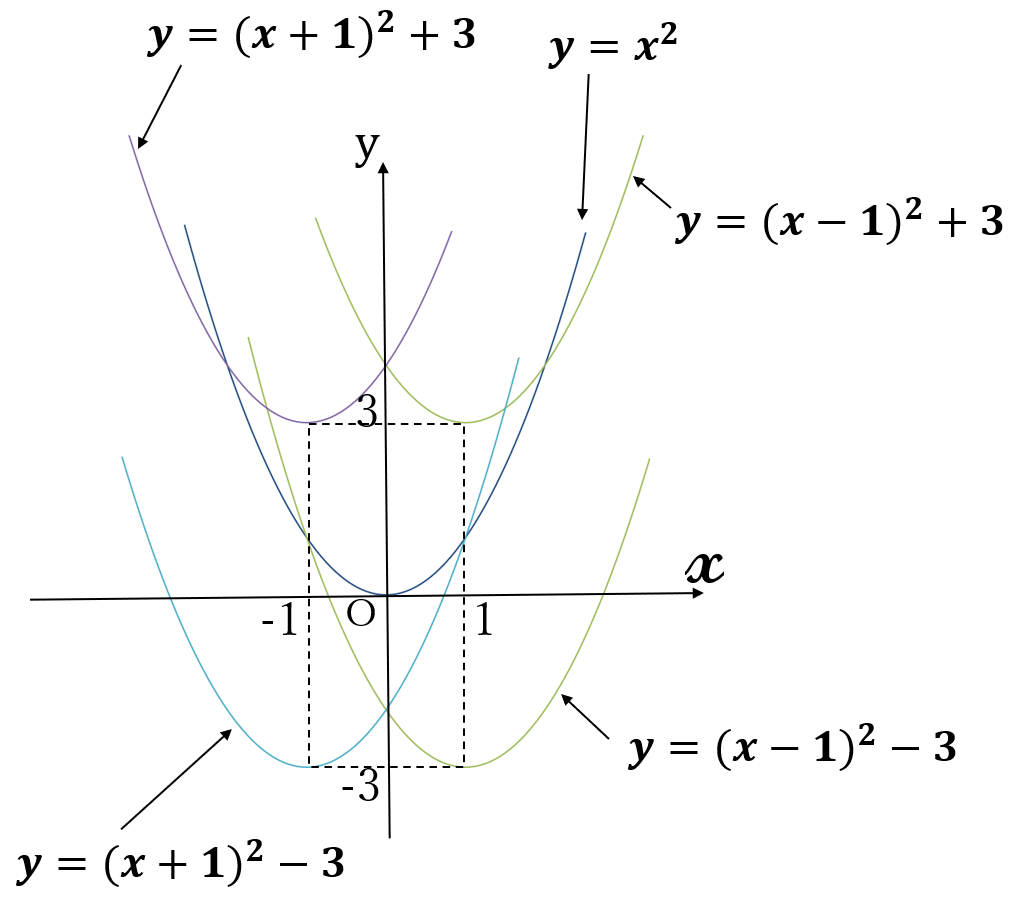
例4の4つの放物線と放物線\( \ y=x^2 \ \)
をまとめて描きます。
例5
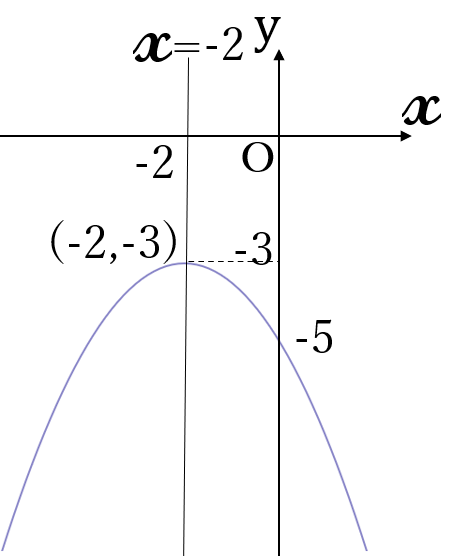
(1) \(\large y=-\frac{1}{2}(x+2)^2-3\)
\(y=a(x-p)^2+q \ \)の形にします。
\(y=-\frac{1}{2}\{x-(-2)\}^2+(-3) \ \)ですから、
\(p=-2, \ q=-3 \ \)です。したがって、
\(y=-\frac{1}{2}x^2 \ \)のグラフを、
\(x \ \)軸方向に\(-2\)、\(y \ \)軸方向に\(-3 \ \)だけ
平行移動したグラフです。
\(a=-\frac{1}{2} \lt 0 \ \)ですから、
上に凸の放物線です。
軸 \(x=-2\)
頂点 \((-2, \ -3)\)
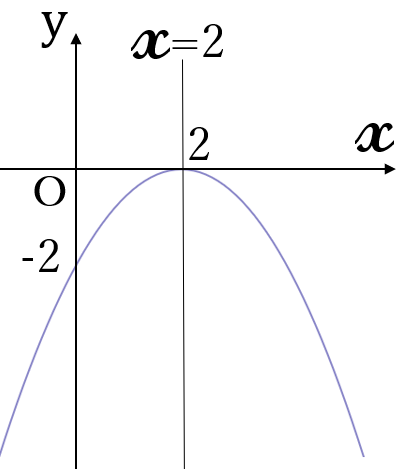
(2) \(\large y=-\frac{1}{2}(x-2)^2\)
\(y=a(x-p)^2+q \ \)の形にします。
\(y=-\frac{1}{2}(x-2)^2+0 \ \)ですから、
\(p=2, \ q=0 \ \)です。したがって、
\(y=-\frac{1}{2}x^2 \ \)のグラフを、
\(x \ \)軸方向に\( \ 2 \ \)だけ平行移動したグラフです。
\(a=-\frac{1}{2} \lt 0 \ \)
ですから、
上に凸の放物線です。
軸 \(x=2\)
頂点 \((2, \ 0\)
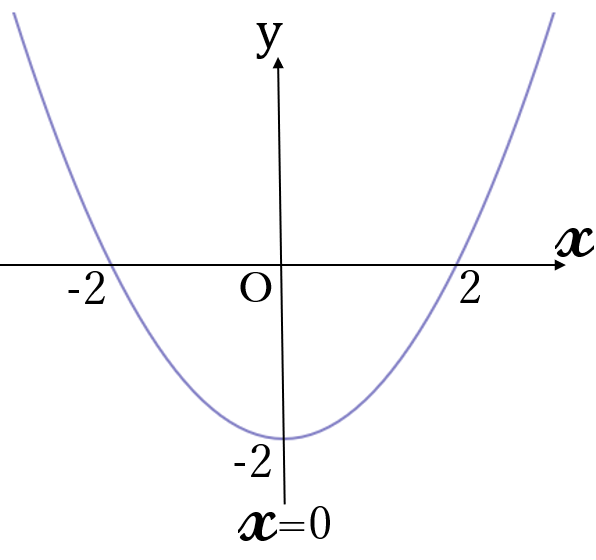
(3) \(\large y=\frac{1}{2}x^2-2\)
\(y=a(x-p)^2+q \ \)の形にします。
\(y=\frac{1}{2}(x-0)^2+(-2) \ \)ですから、
\(p=0, \ q=-2 \ \)です。したがって、
\(y=\frac{1}{2}x^2 \ \)のグラフを、
\(y \ \)軸方向に\( \ -2 \ \)だけ平行移動したグラフです。
\(a=\frac{1}{2} \gt 0 \ \)
ですから、
下に凸の放物線です。
軸 \(x=0 \ \)(\(y \ \)軸)
頂点 \((0, \ -2)\)
注意点3
\(\Large y=ax^2+q\) や \(\Large y=a(x-p)^2\) は、
\(\Large y=a(x-p)^2+q\) の特別な場合です。
\(\Large y=a(x-p)^2+q\) において
\(\Large p=0\) のとき、\(\Large y=ax^2+q\)
放物線の頂点は、\(y \ \)軸上にあります。
\(\Large q=0\) のとき、\(\Large y=a(x-p)^2\)
放物線の頂点は、\(x \ \)軸上にあります。
注意点4
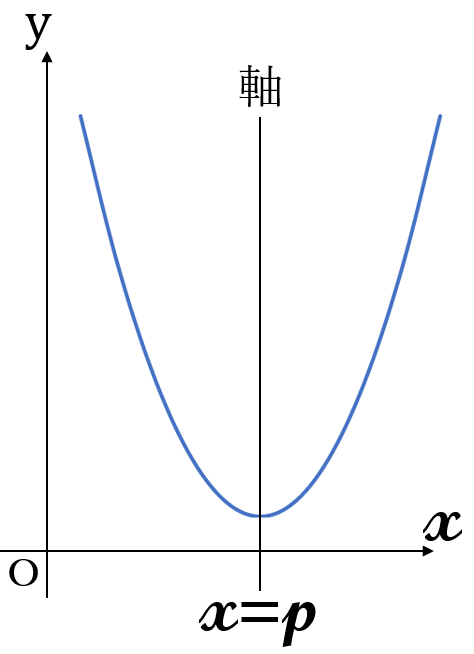
放物線の頂点を通り、
\(x \ \)軸に垂直な直線を、
「放物線の軸」
といいます。
放物線の軸の方程式は、
「\(x= \ \)定数」
という形になります。
このことに抵抗のある生徒が多いです。
「\(x=p \ \)(定数)」
は、\(xy \ \)座標平面上では、直線を表してます。
「すべての\( \ y \ \)の値に対して、つねに\( \ x \ \)の値は\( \ p \ \)である点の集まり」で、\(x \ \)軸に垂直な直線になります。
方程式の解である 「\(x=\)定数」 とは意味が違います。
それでは、例を参考にして、例題をやってみましょう。筆記用具が無くても大丈夫です。スマホの画面を見ながら、解法を目で追ってください。頭の中でグラフ(放物線)をイメージするだけで良いです。
