問題48
下の図で、
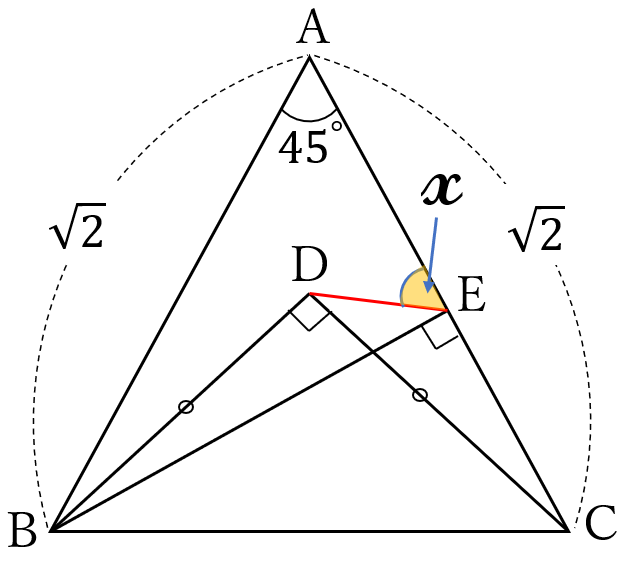
\(AB=AC=\sqrt{2}, \ \angle BAC =45^{\circ}, \ BE \perp AC \ \)
です。
\(\triangle DBC \ \)は、\(\angle BDC =90^{\circ}, \ DB=DC \ \)
の直角二等辺三角形です。
このとき、\(\angle AED \ \)の大きさ\(\Large \ x \ \)と、線分\( \ DE \ \)の長さを求めなさい。
解答
(答) \(\Large x(\angle AED) =45^{\circ}, \ DE=\sqrt{2}-1\)
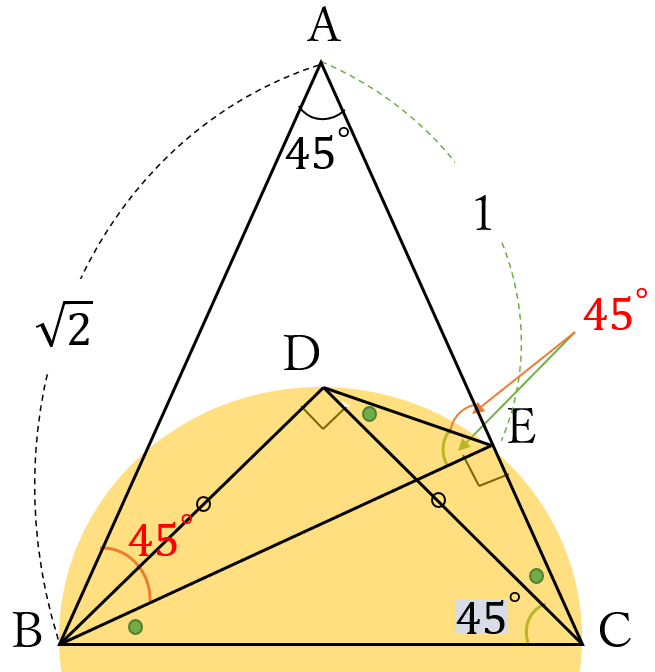
\(\angle BDC =\angle BEC \)
\(=90^{\circ} \ \)だから
点\( \ B, \ D, \ E, \ C \ \)
は、線分\(BC \ \)を直径
とする円周上に
あります。
よって、
円周角の定理より
\(\angle DCB =\angle DEB\)
\(=45^{\circ}\)
\(BE \perp AC \ \)ゆえ
\(\large x(\angle AED)=90^{\circ}-\angle DEB\)
\(\large =90^{\circ}-45^{\circ}\)\(\Large =45^{\circ}\)
\(DE \ \)の解答は次ページ⇒

\(\triangle ABE \ \)は、
\(\angle AEB=90^{\circ} \ \)の
直角二等辺三角形
なので
\(\angle ABE =45^{\circ}\)
\(\angle EBC= \angle ABC-45^{\circ}\)
\(\cdots \ \)①
\(\angle ECD=\angle ACB -45^{\circ}\)
\(\cdots \ \)②
\(\triangle ABC \ \)は、\(AB=AC \ \)の二等辺三角形だから
\(\angle ABC =\angle ACB \ \cdots \ \)③
①②③より、\(\angle EBC =\angle ECD\)
また、円周角の定理より\( \ \angle EBC =\angle EDC \ \)だから
\(\angle EDC= \angle ECD\) よって、
\(\triangle EDC \ \)は、\(ED=EC \ \)の二等辺三角形です。
\(\triangle ABE \ \)は、\(1:1:\sqrt{2} \ \)の直角二等辺三角形だから
\(AE=1\) ゆえに
\(\large DE=EC=AC-AE=\sqrt{2}-1\)
次の問題47は、今年(令和4年)の埼玉県高校入試問題を、解きやすいようにアレンジしたものです。高校の教科書に出てくるような問題ですが、中学で勉強した知識で解くことができます。
埼玉県の原文は、参考問題として、問題47の後に掲載しておきました。
問題50
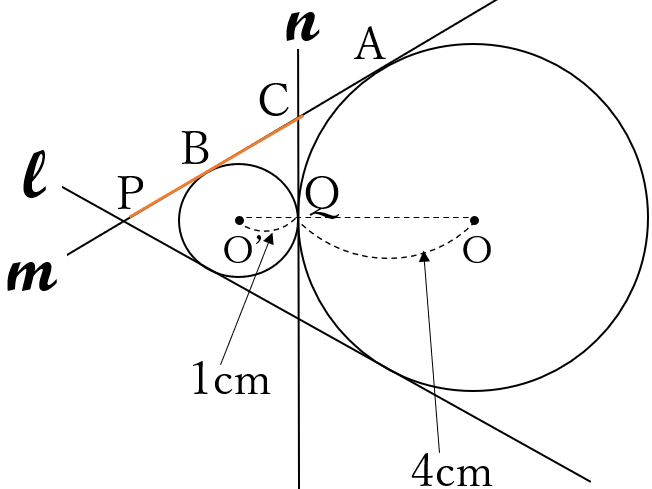
下の図のように、半径\(4cm\)の円\(O\)と半径\(1cm\)の円\(O’\)が接しています。円\(O\)の中心を\(O\)、円\(O’\)の中心を\(O’\)、二つの円の接点を\(Q\)とします。また、二つの円の共通接線は3本ありますが、下の図のように3本の接線をそれぞれ、\(l,m,n\)とします。接線\(m\)と円\(O\)、円\(O’\)の接点をそれぞれ\(A,B\)、接線\(m\)と接線\(l\)、接線\(n\)の交点をそれぞれ\(P,C\)とします。このとき、線分\(PC\)の長さを求めてください。
解答
(答)\(\Large \frac{10}{3}\)\((cm)\)
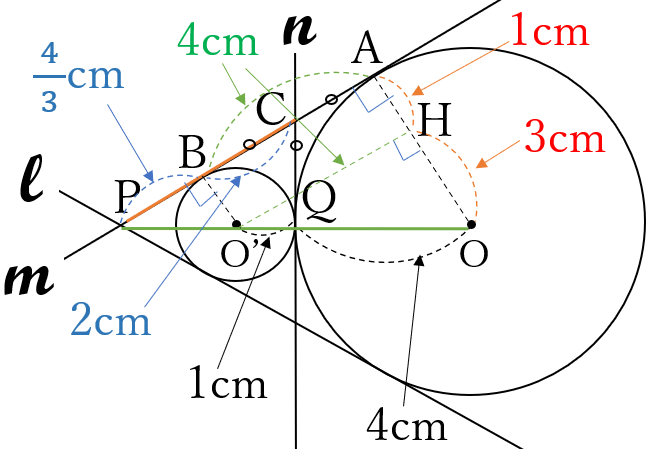
点\(O\)と点\(A\)、
点\(O’\)と点\(B\)
を結びます。
点\(O’\)から線分\(OA\)に引いた垂線と線分\(OA\)との交点を\(H\)とします。
\(\triangle HO’O \ \)は、\(3:4:5 \ \)の直角三角形だから、
\(O’H=4cm\) また、\(OA \perp m, \ O’B \perp m \ \)より、
四角形\(ABO’H\)は長方形です。よって、
\(BO’=AH=1cm, \ AB=O’H=4cm \ \cdots \ \)①
\(OH=3cm\) ここで、\(CA=CQ, \ CB=CQ \ \)ゆえ
\(CA=CB\) したがって①より、\( \ CB=2cm \ \cdots \ \)②
さらに、\(\triangle HO’O \ \)∽\( \ \triangle BPO’ \ \)で、相似比は
\(OH:O’B=3:1 \ \)だから、\(BP=\frac{1}{3}O’H=\frac{4}{3}cm\)
②より、\(PC=BP+CB=\)\(\large \frac{4}{3}+2=\frac{10}{3}\) \((cm)\)
参考問題
令和4年 埼玉県高校入試問題
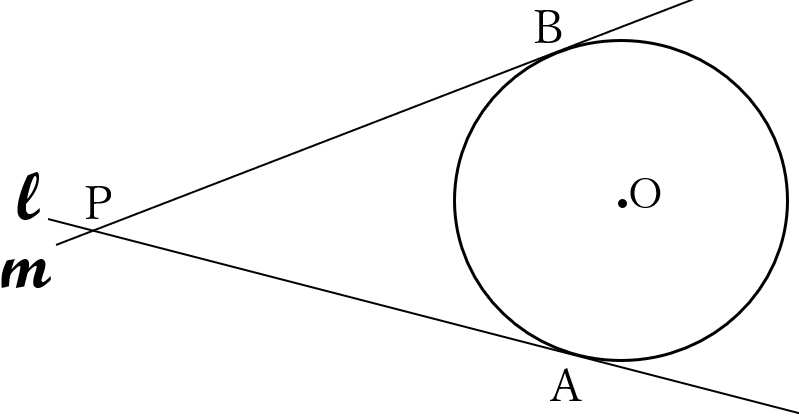
下の図のように、点\( \ O \ \)を中心とする円\( \ O \ \)の円周上に2点\( \ A, \ B \ \)をとり、\( \ A, \ B \ \)を通る円\( \ O \ \)の接線をそれぞれ\( \ l, \ m \ \)とします。
直線と\( \ l \ \)と\( \ m \ \)が点\( \ P \ \)で交わるとき、次の各問に答えなさい。
(1) \(PA=PB \ \)であることを証明しなさい。
(2)は、次ページ⇒
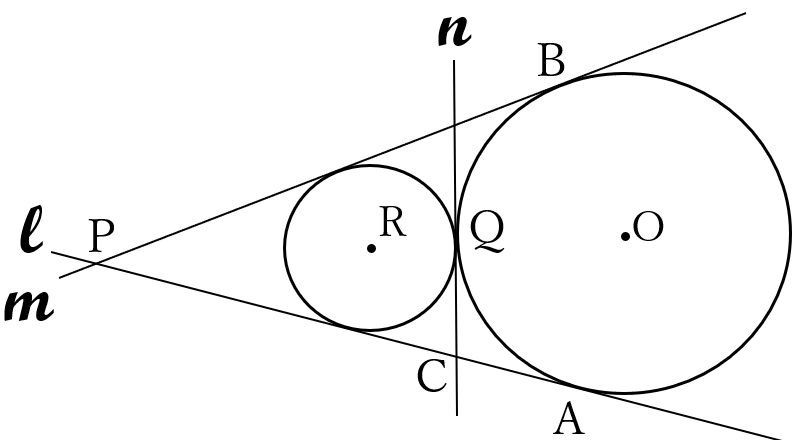
(2) 下の図のように、直線\( \ l, \ m \ \)に接し、円\( \ O \ \)に点\( \ Q \ \)で接する円の中心を\( \ R \ \)とします。また、点\( \ Q \ \)を通る円\( \ O \ \)と円\( \ R \ \)の共通接線を\( \ n \ \)とし、\( \ l \ \)と\( \ n \ \)の交点を\( \ C \ \)とします。
円\( \ O \ \)の半径が\( \ 5cm \ \)、円\( \ R \ \)の半径が\( \ 3cm \ \)であるとき、線分\( \ PC \ \)の長さを求めなさい。
解答
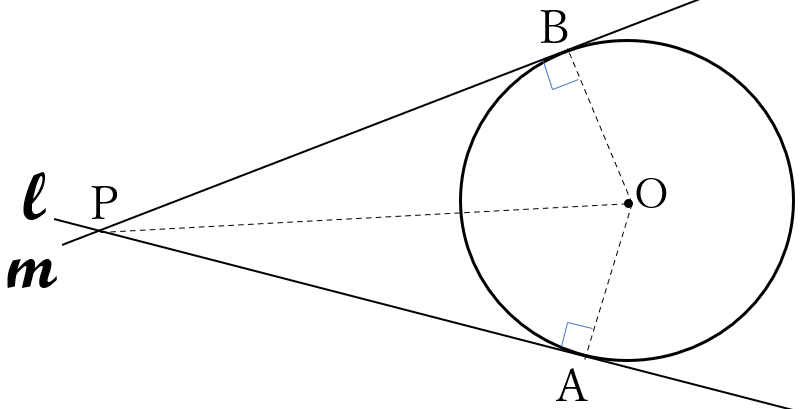
(1) (証明) (例)
\(\triangle APO \ \)と\( \ \triangle BPO \ \)において
\(PO \ \)は共通\( \ \cdots \ \)①
円の半径なので、\(OA=OB \ \cdots \ \)②
\(A, \ B \ \)は接点なので、
\(\angle PAO=\angle PBO =90^{\circ} \ \cdots \ \)③
①②③から、
直角三角形で、斜辺と他の1辺がそれぞれ等しいので、
\(\triangle APO \equiv \triangle BPO\)
したがって、\(PA=PB\)
(2)の解答は次ページ⇒
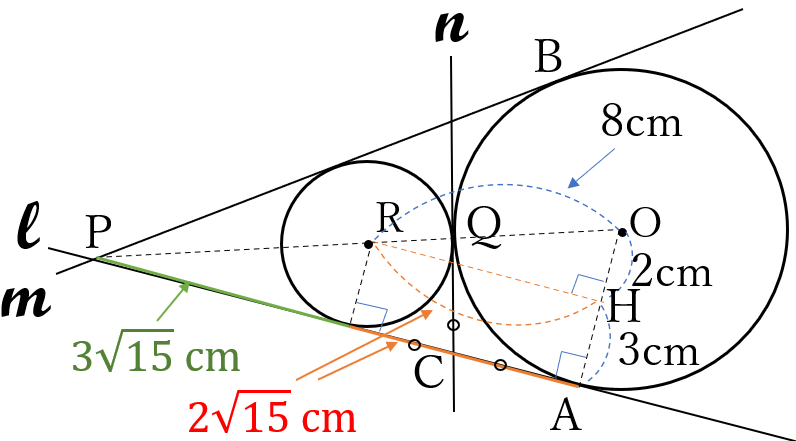
(2) \(\Large 4 \sqrt{15}\) \((cm)\)
問題50と同様に求められます。
詳細な解答は省略します。
下図を参考にして解いてみてください。
\(RH\)は、三平方の定理で求めます。
問題18
下の図のように、円\(O \ \)があります。円\(O \ \)の中心を\(O \ \)とします。線分\(AB \ \)は円\(O \ \)の直径です。直線\(l \ \)は、円\(O \ \)に接しています。接線\(l \ \)と円\(O \ \)との接点を\(C \ \)とし、接線\(l \ \)と直線\(AB \ \)との交点を\(P \ \)とします。また、点\(A \ \)と点\(C \ \)とを結びます。
\(\angle APC=30^{\circ} \ \)のとき、\(\angle ACP \ \)の大きさ\(\large x \ \)を求めなさい。
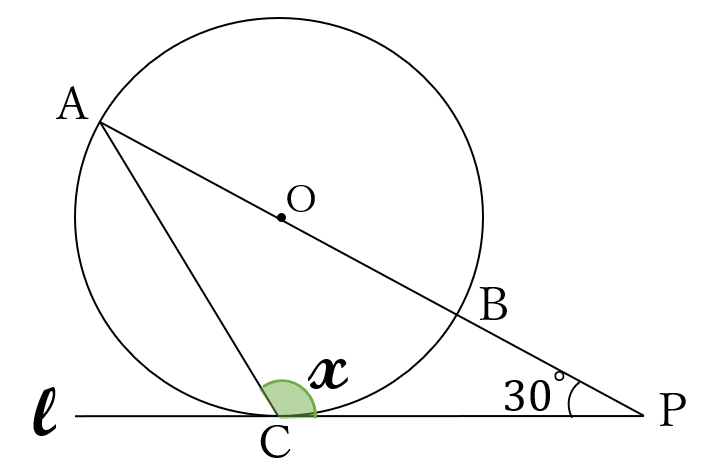
解答
(答) \(\Large 120^{\circ}\)
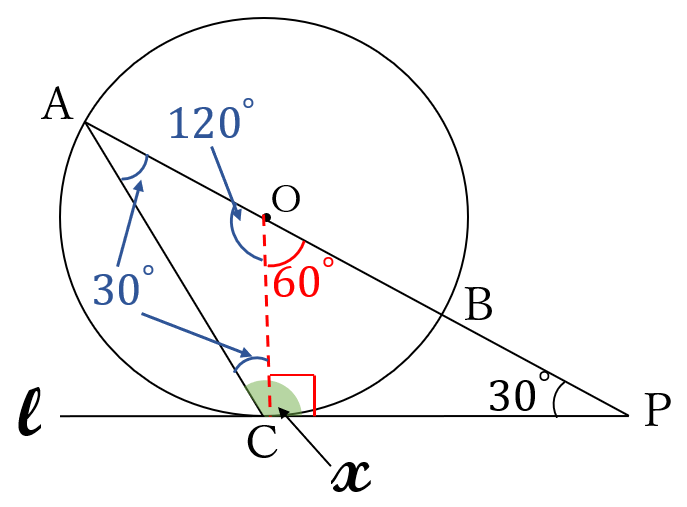
円の中心\(O \ \)と接点\(C \ \)を結びます。
\(OC \perp l \ \)より、\(\angle POC =60^{\circ}\)
\(\triangle OAC \ \)は二等辺三角形だから、
\(\angle OAC =\angle OCA=30^{\circ}\)
よって、\(\Large x\)\((\angle ACP)=90^{\circ}+30^{\circ}=120^{\circ}\)
次の問題は、ある県の高校入試の過去問題です。計算というよりは、発見です。
問題51
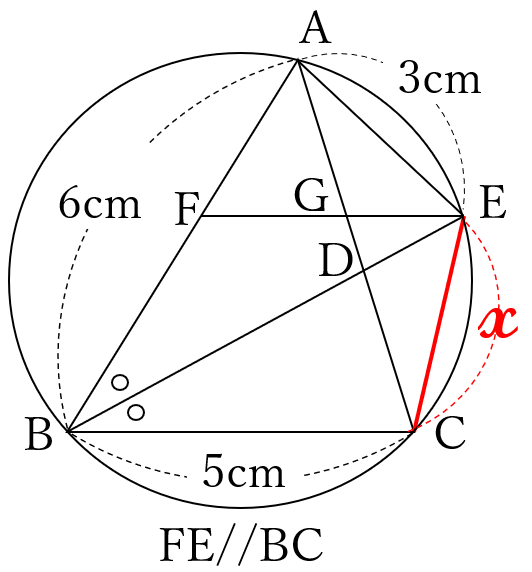
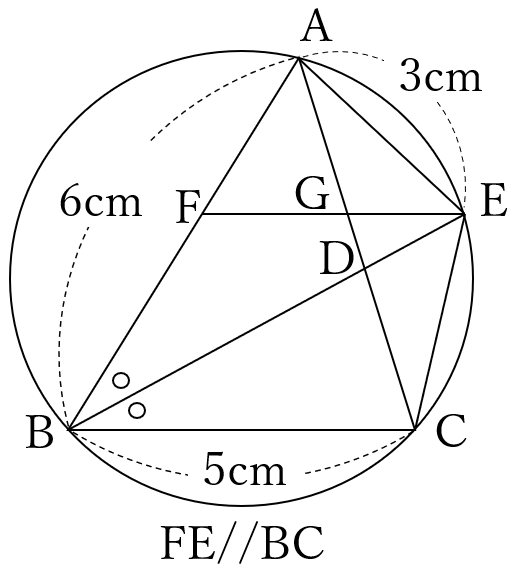
右の図のように、円周上の点\(A, \ B, \ C \ \)を頂点とする\(\triangle ABC \ \)があり、\(\angle ABC \ \)の二等分線と線分\(AC \ \)との交点を\(D\)、円との交点のうち点\(B \ \)と異なる点を\(E \ \)とします。また、線分\(AB \ \)上に点\(F \ \)を、\(EF//CB \ \)となるようにとり、線分\(EF \ \)と線分\(AC \ \)との交点を\(G \ \)とします。さらに、点\(A \ \)と点\(E \ \)、
点\(C \ \)と点\(E \ \)をそれぞれ結びます。
\(AB=6cm, \ BC=5cm, \ AE=3cm \ \)であるとき、
次の問いに答えなさい。
(1) 線分\(CE \ \)の長さを求めなさい。
(2) \(ED:DG \ \)を最も簡単な整数比で答えなさい。
解答
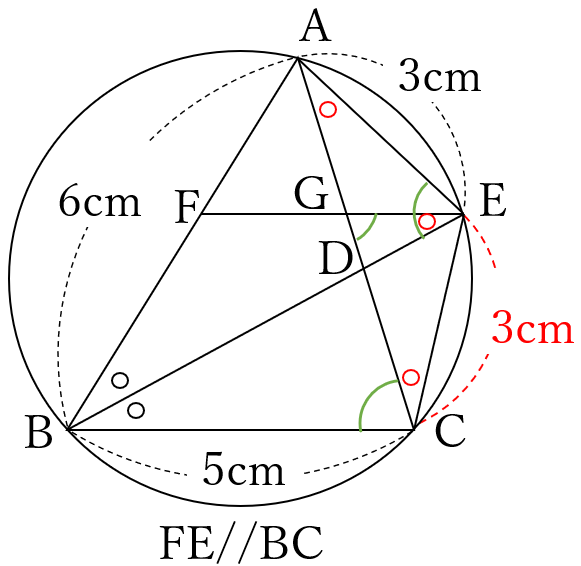
(1) \(\Large 3\) \((cm)\)
弧\(AE \ \)の円周角より
\(\angle ABE =\angle ECA\)
弧\(EC \ \)の円周角より
\(\angle EBC =\angle EAC\)
\(\angle ABE =\angle EBC\)
だから、
\(\angle ECA =\angle EAC\)
よって、\(\triangle EAC \ \)は
二等辺三角形
ゆえに、\(EC=EA=3cm\)
(2)の解答は次ページ
解答
(2) \(\Large ED:DG=2:1\)

弧\(AB \ \)の円周角より
\(\angle ACB =\angle AEB\)
\(\cdots\)①
\(\angle ACB =\angle EGD\)
\(\cdots\)②(錯角)
\(\angle EBC =\angle FEB\)
\(\cdots\)③(錯角)
与条件より
\(\angle EBC =\angle ABE\)
\(\cdots\)④
よって、\(\triangle ABE \ \)と\( \ \triangle DEG \ \)において
①②より、\(\angle AEB =\angle EGD \ \cdots\)⑤
③④より、\(\angle ABE =\angle DEG \ \cdots\)⑥
⑤⑥より2組の角が等しいので、\(\triangle ABE \ \)∽\( \ \triangle DEG\)
ゆえに、\(\large ED:DG=BA:AE=6:3\)
⇩ 次の文章は、Wordで
問題49は、ある県の高校入試の過去問題ですが、他に証明問題と(3)があります。証明問題は基本的な問題なのですが、(3)は、難問になっています。暗算では厳しいので、参考問題として掲載します。
参考問題
右の図のように、円周上の点\(A, \ B, \ C \ \)を頂点とする\(\triangle ABC \ \)があり、\(\angle ABC \ \)の二等分線と線分\(AC \ \)との交点を\(D\)、円との交点のうち点\(B \ \)と異なる点を\(E \ \)とします。また、線分\(AB \ \)上に点\(F \ \)を、\(EF//CB \ \)となるようにとり、線分\(EF \ \)と線分\(AC \ \)との交点を\(G \ \)とします。さらに、点\(A \ \)と点\(E \ \)、点\(C \ \)と点\(E \ \)をそれぞれ結びます。①、②に答えなさい。
① \(\triangle ABD \ \)∽\( \ \triangle ECD \ \)を証明しなさい。
② \(AB=6cm, \ BC=5cm, \ AE=3cm \ \)
であるとき、次の問いに答えなさい。
(1) 線分\(CE \ \)の長さを求めなさい。
(2) \(ED:DG \ \)を最も簡単な整数比で答えなさい。
(3) 線分\(AF \ \)の長さを求めなさい。
解答

①
\(\triangle ABD \ \)と\( \ \triangle ECD \ \)
において
弧\(AE \ \)の円周角より
\(\angle ABD = \angle ECD\)
\(\cdots\)①
\(\angle ADB =\angle EDC\)
\(\cdots\)②(対頂角)
①②より
2組の角が等しいので、
\(\triangle ABD \ \)∽\( \ \triangle ECD\)
(証明終わり)
②(3)の解答は次ページ⇒

②(3) \(\Large \frac{27}{11}\) \((cm)\)
弧\(AB \ \)の円周角より
\(\angle ACB =\angle AEB\)
\(\cdots\)①
\(\angle ACB =\angle EGD\)
\(\cdots\)②(錯角)
\(\angle EBC =\angle FEB\)
\(\cdots\)③(錯角)
弧\(EC \ \)の円周角より、\(\angle EBC =\angle EAC \ \cdots\)④
\(\triangle ADE \ \)と\( \ \triangle EDG \ \)において、①②より
\(\angle AED =\angle EGD\)、③④より\(\angle EAD =\angle GED\)
2組の角が等しいので、\(\triangle ADE \ \)∽\( \ \triangle EDG\)
(2)より、\(ED:DG=2:1, \ AD:DE=2:1\)
よって、\(AD:DG=4:1 \ \cdots\)⑤
\(BD\)は\(\angle ABC\)の二等分線だから、
\(AD:DC=6:5 \ \cdots\)⑥
⑤⑥より \(AG=\frac{3}{4}AD, \ AD=\frac{6}{11}AC\)
\(\iff AG=\frac{3}{4} \cdot \frac{6}{11}AC=\frac{9}{22}AC\)
\(FG//BC\)ゆえ\(AF=\frac{9}{22}AB=\frac{9}{22} \times 6\)\(\large =\frac{27}{11}\)
問題22
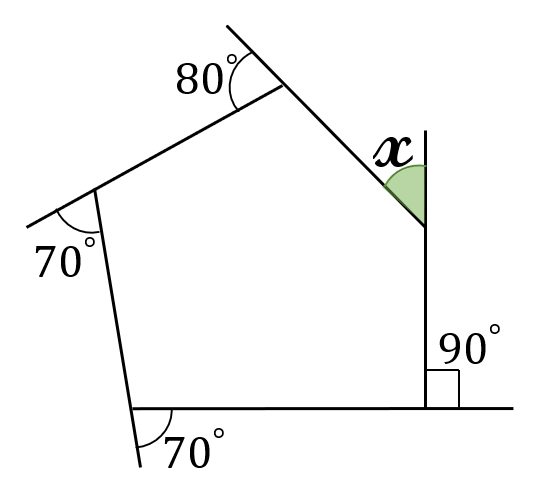
下の図で、\(\angle \ \)\(\large x \ \)の大きさを求めなさい。
解答
(答) \(\Large 50^{\circ}\)
\(n\)角形の内角の和は、\(180^{\circ} \times (n-2)\)
\(n\)角形の外角の和は、\(360^{\circ}\) です。
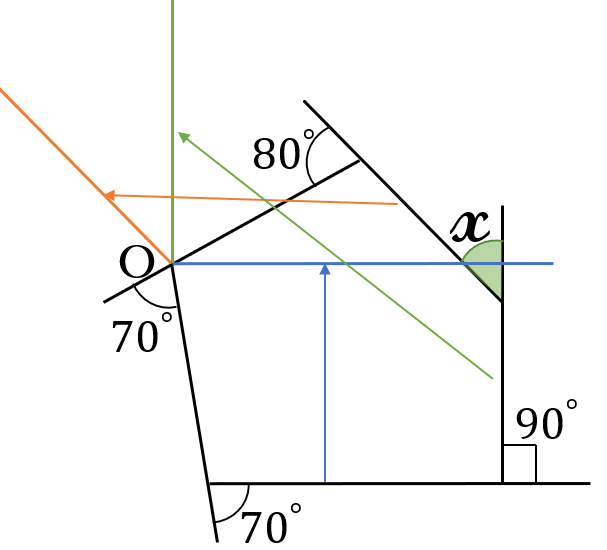
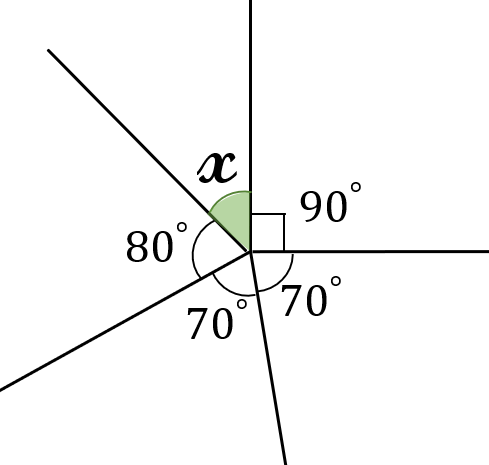
下の図のように、5角形の各辺を点\(O\)に移動させると、外角の和が\(360^{\circ}\)になることが確認できます。
したがって、
\(x=360^{\circ}-80^{\circ}-70^{\circ}-70^{\circ}-90^{\circ}=50^{\circ}\)
次の問題は、よく見かける図形問題で、ある県の2022年度入試問題でも出題されました。
問題26
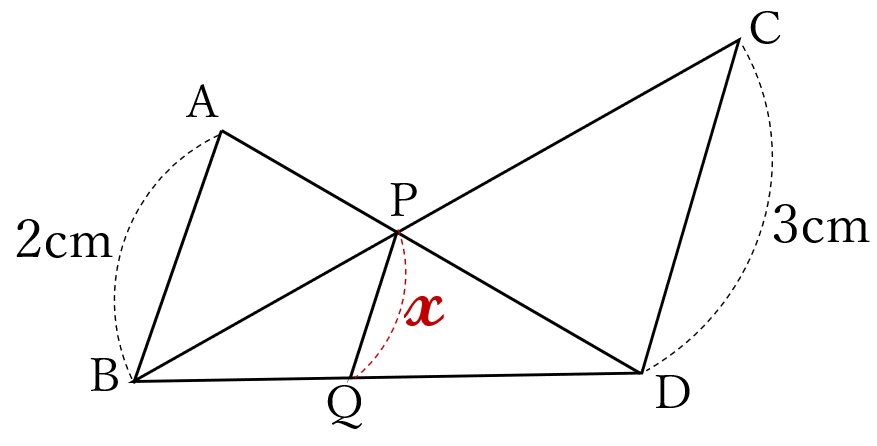
下の図で、
\(AB//PQ//CD, \ AB=2cm, \ CD=3cm\)
のとき、線分\(PQ \ \)の長さ\(\Large x \ \)を求めなさい。
解答
(答) \(\Large \frac{6}{5}\) \((cm)\)
\(AB//CD\)より、\(\triangle PAB \ \)∽\( \ \triangle PDC \ \)だから
\(AB:DC=2:3 \iff AP:PD=2:3\)
よって、\(\triangle DAB \ \)と\( \ \triangle DPQ \ \)において、
\(AB//PQ \ \)より、\(\triangle DAB \ \)∽\( \ \triangle DPQ \ \)
\(DA:DP=5:3 \iff AB:PQ=5:3\)
よって、\(DP \ \)は、\(DA \ \)の\( \ \frac{3}{5} \ \)倍
ゆえに\(PQ \ \)も、\(AB \ \)の\( \ \frac{3}{5} \ \)倍
\(PQ=AB \times \frac{3}{5}=2\times \frac{3}{5}=\)\(\large \frac{6}{5}\)
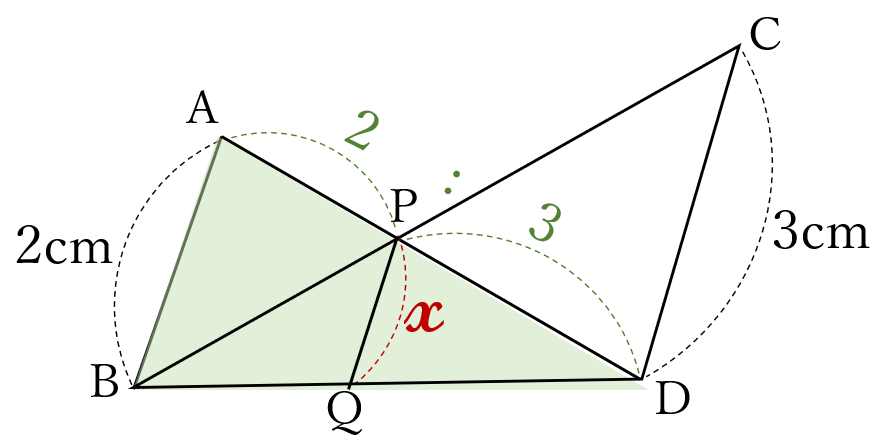
比
\( \ 2:x=5:3\)
から始めようとすると、暗算では厳しいかもしれません。
問題19
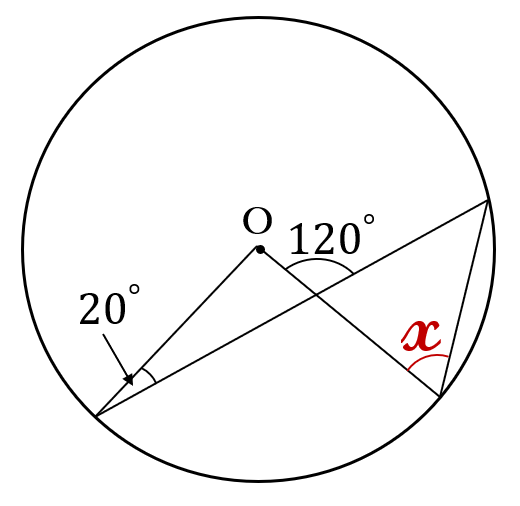
下の図で、\(\angle x\)の大きさを求めなさい。ただし、\(O \ \)は、円の中心です。
解答
(答) \(\Large 70^{\circ}\)
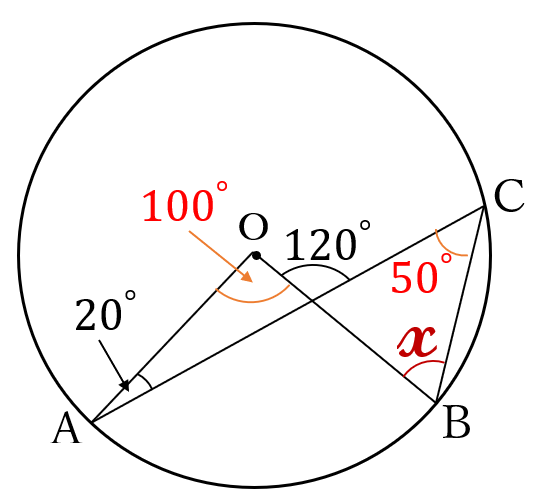
右の図のように、
円周上の点を、
\(A, \ B, \ C\)
とします。
\(\angle AOB + \angle OAC \)
\(=120^{\circ}\)
\(\angle AOB = 120^{\circ}-20^{\circ}\)
\(=100^{\circ}\)
よって、\(\angle ACB =\frac{1}{2} \angle AOB =\frac{1}{2} \times 100^{\circ}=50^{\circ}\)
\(50^{\circ} +x =120^{\circ}\)
\(x=120^{\circ}-50^{\circ}\)\(\Large =70^{\circ}\)
問題53
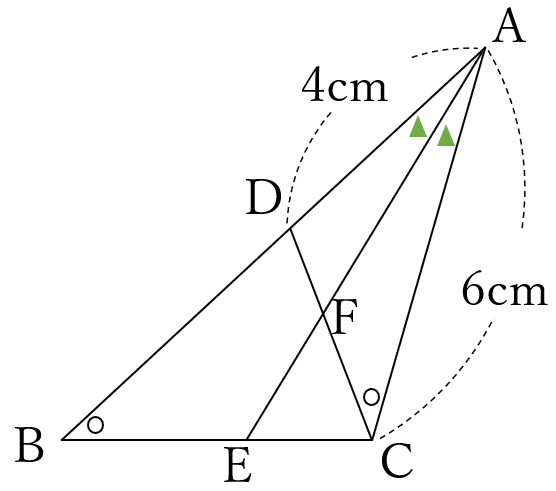
☆☆
右の図のように、
\(\triangle ABC \ \)の辺\( \ AB\)上に、
\(\angle ABC=\angle ACD \ \)となる点\(D \ \)をとります。
また、\(\angle BAC \ \)の二等分線と
辺\(BC\)、線分\(DC \ \)との交点を
それぞれ\(E, \ F \ \)とします。
\(AD=4cm,AC=6cm\)であるとき、
次の問いに答えなさい。
(1)線分\(DB\)の長さを求めなさい。
(2)\(\triangle ABC\)の面積が\(18cm^2\)であるとき、\(\triangle FEC\)の面積を求めなさい。
三角形の内角の二等分線が描かれている
面積問題です。頻出事項なので
しっかり解けるようにしておきましょう。
《参考》
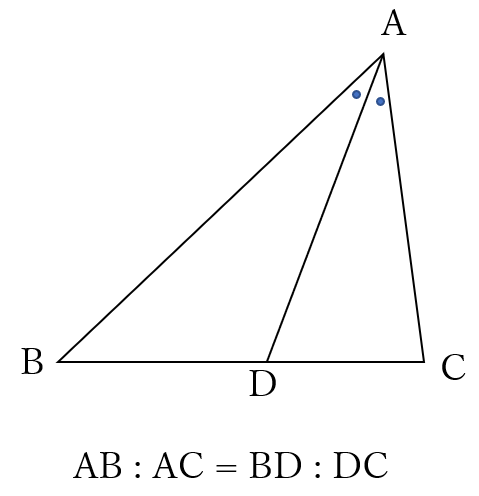
三角形の内角の二等分線と辺の比
右の図の\(\triangle ABC\)において\(\angle BAC\)の内角の二等分線と辺\(BC\)との交点を\(D\)とすると
\(AB:AC=BD:DC\)
である
証明は巻末資料
解答例
(1) \(\triangle ABC \ \)∽\( \ \triangle ACD\)だから
\(AB:AC=AC:AD\) よって
\( AB:6=6:4,\quad AB=9\)
したがって \( DB=5\)
(答) \(5\) \((cm)\)
(2) \(\triangle ABC \times \frac{5}{9} \times \frac{2}{5} \times \frac{3}{5} \ \cdots \ (\ast)\)
\(=18\times \frac{2}{3\times 5}=\frac{12}{5} \)
(答) \(\large \frac{12}{5}\) \((cm^2)\)
(補足)
(2)の解答例\((\ast)\)の計算は
\(\triangle ABC \rightarrow \triangle DBC \rightarrow \triangle DEC \rightarrow \triangle FEC\)の順で
「辺と辺の長さの比」をかけていってます。「辺と辺の長さの比」は
\(DB:AB=5:9, \ EC:BC=2:5, \ FC:DC=3:5\)
