関東地区から北上し、福島県。福島県公立高校入試の令和3年の問題は、何故かまだ公開されていない(2021年4月10日現在)。そこで、昨年度の入試問題から気になる問題を見つけたので、それを解答してみたい。最後の大問7(3)。難問と言っていい問題である。じっくりと考える時間も含め、15分は欲しい。

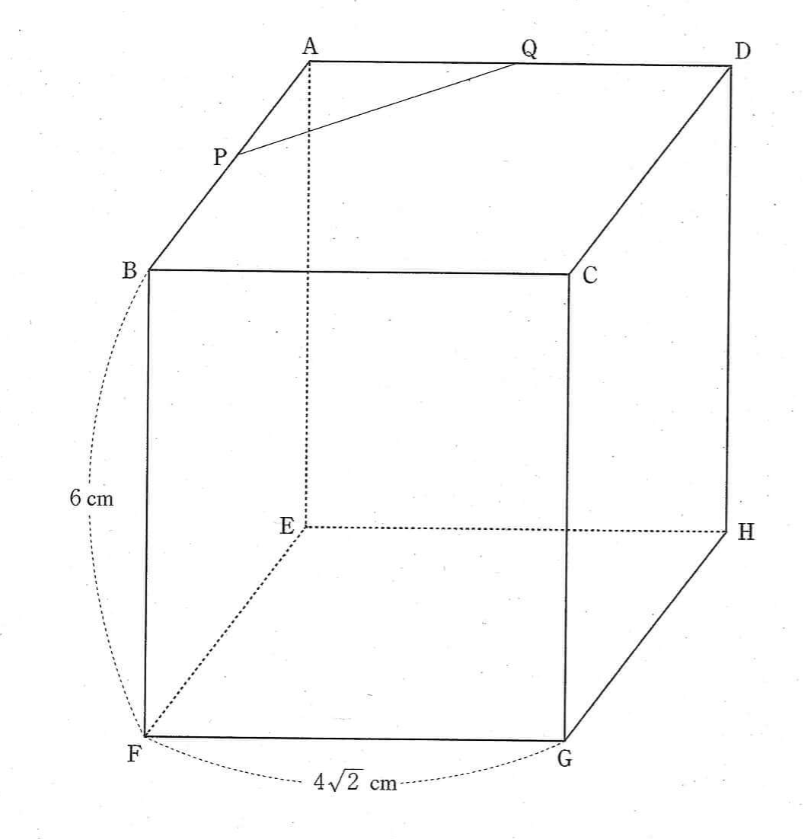
(3)を解くためには、(1)(2)を解く必要があるので、(1)から解いていく。
解答例
(1) 点 \(P, \quad Q\) は、それぞれ
\(AB,\quad AD\) の中点だから
\(AP=AQ=2 \sqrt{2}\)
\(AP:AQ:PQ=1:1:\sqrt{2}\) だから
\(PQ=\sqrt{2} \times 2\sqrt{2}=4\)
(答) \(4 \quad (cm)\)
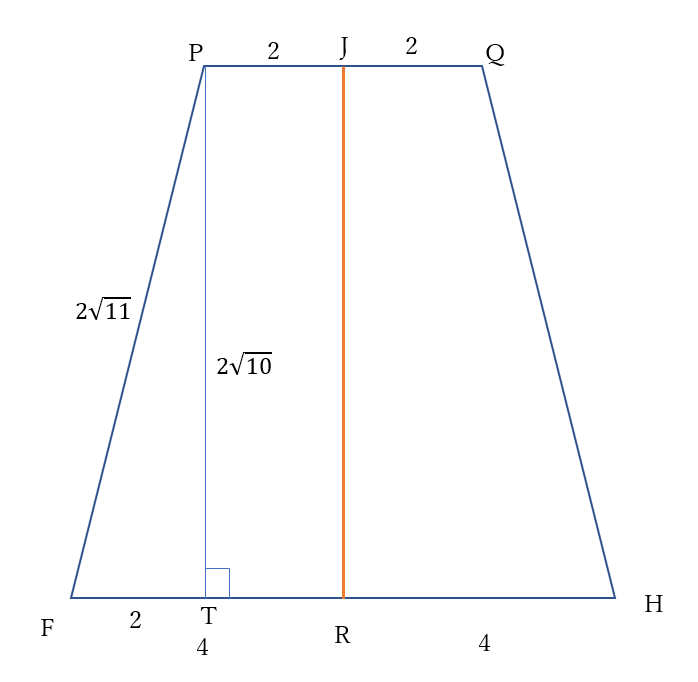
(2) \(FH=8\)
\(PF=\sqrt{PB^2+BF^2}\)
\(=\sqrt{(2\sqrt{2})^2+6^2}=\sqrt{48}=2\sqrt{11}\)
点\(P\)から辺\(FE\)に下した垂線の足を\(T\)とすると
\(PT=\sqrt{PF^2-FT^2}\)
\(=\sqrt{(2\sqrt{11})^2-2^2}=\sqrt{40}=2\sqrt{10}\)
よって、求める四角形\(PFHQ\)の面積は、
\((PQ+FH) \times PT \times \frac{1}{2}\)
\(=(4+8) \times 2\sqrt{10} \times \frac{1}{2}=12\sqrt{10}\)
(答) \(12\sqrt{10}\) \((cm^2)\)
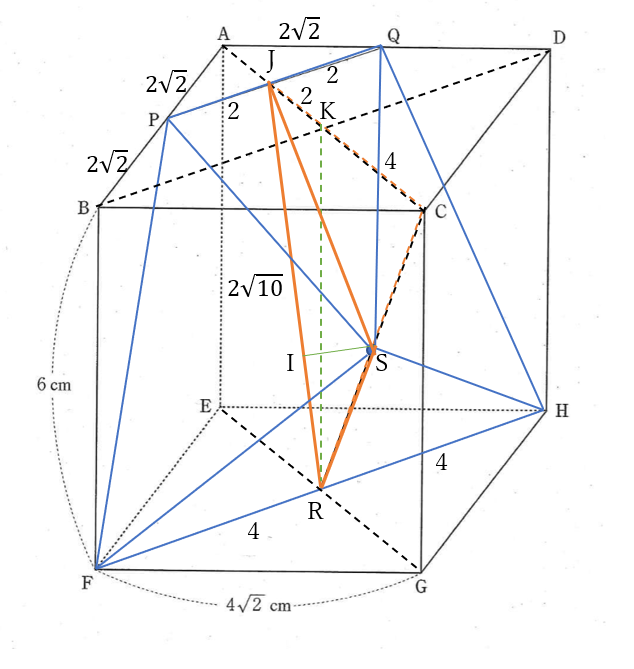
(3) 求める体積は、\(S\)を頂点とした底面\(PFHQ\)の四角錐だから、求める体積は
(底面\(PFHQ\)の面積)\(\times\)(高さ)\(\times \frac{1}{3}\)
底面\(PFHQ\)の面積は、(2)で求めているから、この四角錐の高さを求める。
右の図のように、線分\(PQ\)の中点を\(J\)、線分\(AC,BD\)の交点を\(K\)とする。
頂点\(S\)から線分\(JR\)に下した垂線の足を\(I\)とすると、\(SI\)がこの四角錐の高さである。
\(\triangle SJR\)の面積は、\(\triangle CJR\)の面積の\(\frac{1}{2}\)である。
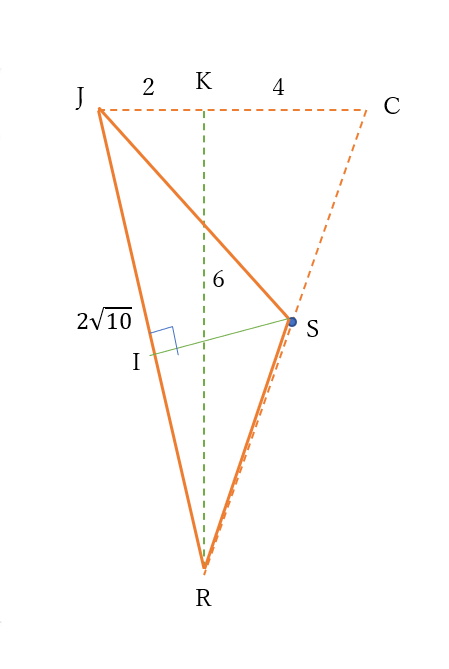
\(\triangle CJR\)の面積は
\(JC \times KR \times \frac{1}{2}\)
ここで、\(KR=6\)
\(JC=JK+KC=2+4=6\) だから
\(\triangle CJR=6 \times 6 \times \frac{1}{2}=18\)
\(\iff \triangle SJR=\frac{1}{2} \triangle CJR=9\)
\(\triangle SJR=JR \times SI \times \frac{1}{2}\) だから
\(JR \times SI \times \frac{1}{2}=9\)
\(\iff 2\sqrt{10} \times SI \times \frac{1}{2}=9\)
\(\iff SI=\frac{9}{\sqrt{10}}\)
よって、求める体積は
(底面\(PFEQ\)の面積)\(\times\)(高さ)\(\times \frac{1}{3}\)
\(=12\sqrt{10} \times SI \times \frac{1}{3}\)
\(=12\sqrt{10} \times \frac{9}{\sqrt{10}} \times \frac{1}{3}\)
\(=36\)
(答) \(36\) \((cm^3)\)
受験生は、四角錐の高さをすんなり求められるだろうか?かなり苦労すると思われる。じっくりと考える時間的余裕はないので、難問と言っていい問題である。
