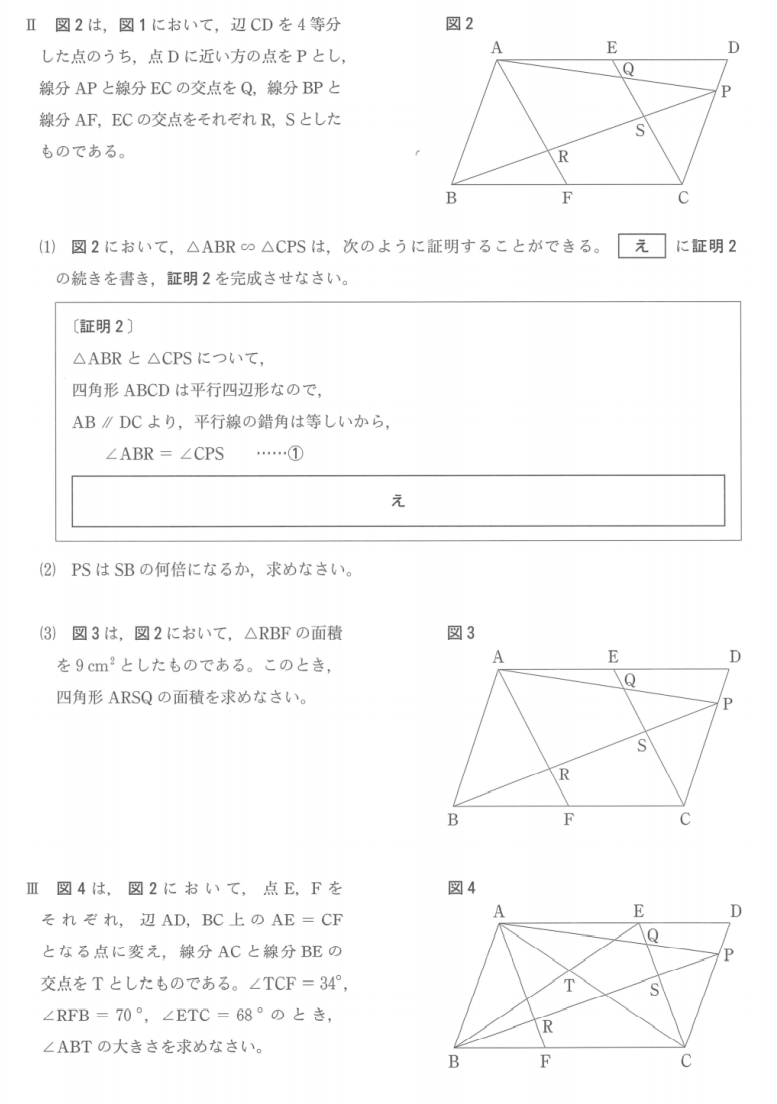
最後の図形問題に少してこずるかもしれない。全体的に基本的な問題が幅広く多数出題されている。計算が複雑になることもないので、できるだけ早くそつなく解答して最後の図形問題に臨めれば高得点が採れそうである。
大問4Ⅱ
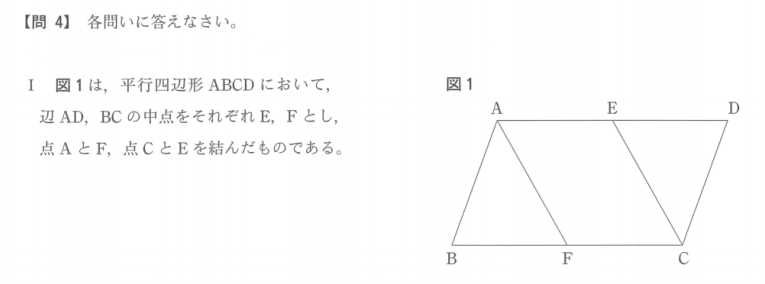
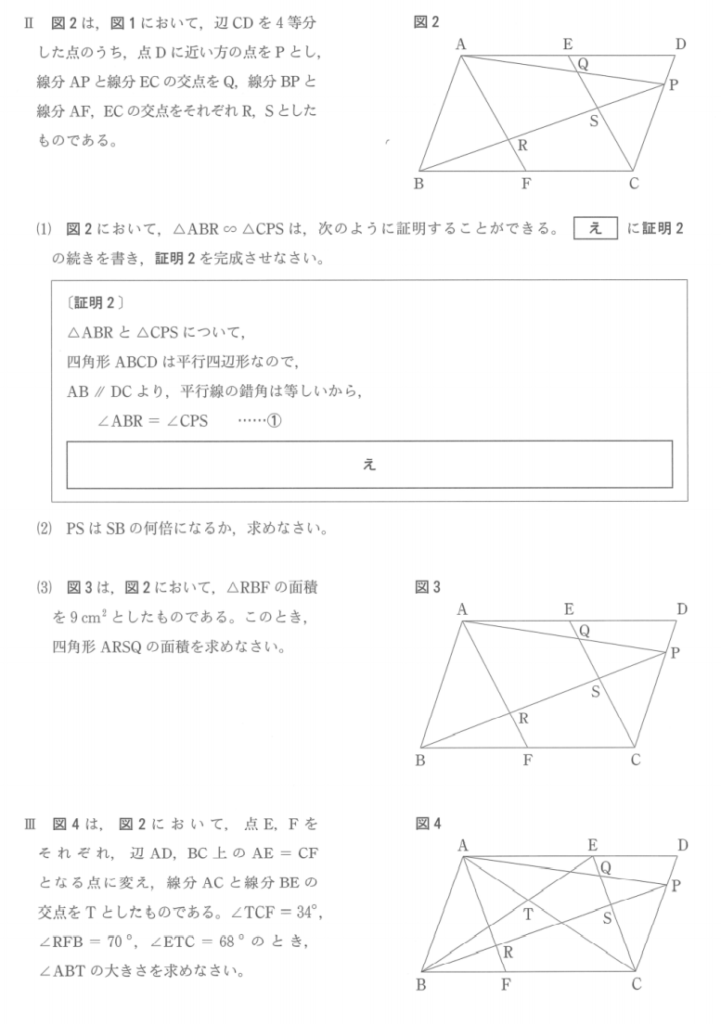
Ⅱ(2)解答例
(1)より、\(\triangle ABR \sim \triangle CPS\)
題意より
\(CP:AB=3:4\)
\(\iff PS:BR=3:4\)
また
\(BF=FC,RF//SC\)
\(\iff BR=RS\)
ゆえに
\(PS:SB=PS:2BR=3:8\)
\(\iff PS=\frac{3}{8}SB\)
(答) \(\large \frac{3}{8}\) (倍)
Ⅱ(3)解答例
\(\triangle RBF=9\)
\(\triangle BRF \sim \triangle BSC,BR=RS\)
\(\iff BS:BR=2:1\)
\( \iff \triangle BSC : \triangle BRF=4:1\)
\(\iff \triangle BSC=9 \times 4=36\)
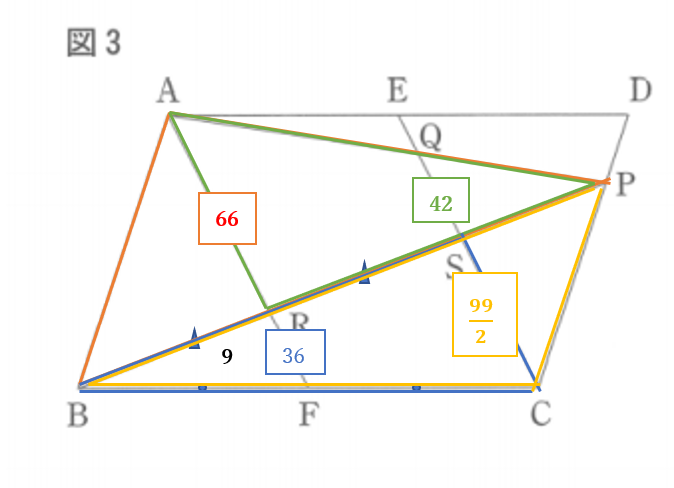
\(PB:SB=11:8\)
\(\iff \triangle BPC=\triangle BSC \times \frac{11}{8}\)
\(=36 \times \frac{11}{8}=\frac{99}{2}\)
\(AB:PC=4:3\)
\(\iff \triangle ABP=\triangle BPC \times \frac{4}{3}\)
\(=\frac{99}{2} \times \frac{4}{3}=66\)
\(BR:RS:SP=4:4:3\)
\( \iff \triangle ARP=\triangle ABP \times \frac{7}{11}\)
\(\iff 66 \times \frac{7}{11}=42\)
\(RP:SP=7:3\)
\(\triangle QSP=\triangle ARP \times (\frac{3}{7})^2\)
\(=\triangle ARP \times \frac{9}{49}\)
\(\iff \)四角形\(ARSQ\)
\(=\triangle ARP \times \frac{40}{49}\)
\(=42 \times \frac{40}{49}\)
\(=\frac{240}{7}\)
Ⅱ(3)(答) \(\large \frac{240}{7}\) \((cm^2)\)
【参考】
相似比の2乗と線分の比を連続して掛け合わせると次のようになります。
\(9\times 4\times \frac{11}{8}\times \frac{4}{3}\times \frac{7}{11}\times \{(1-(\frac{3}{7})^2\}\)
\(=\frac{240}{7}\)
計算の順番は
\(\triangle RBF \rightarrow \triangle SBC \rightarrow \triangle PBC\)
\(\rightarrow \triangle ABP \rightarrow \triangle ARP \rightarrow \triangle ARSQ\)
になってます。
Ⅲ 解答例
\(\angle ETC=68^{\circ},\angle TCF=34^{\circ}\)
\(\iff \angle TBC=34^{\circ}\)
よって
\(\triangle TBC\) は \(TB=TC\)
の二等辺三角形\(\dots\)①
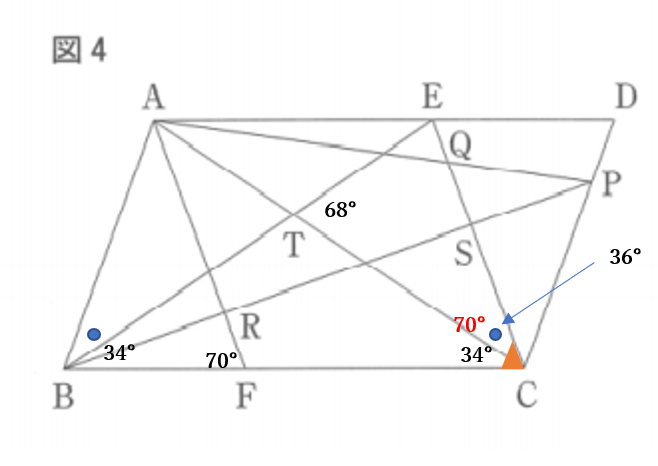
四角形\(AFCE\)は平行四辺形なので
\(\angle ECB=\angle RFB=70^{\circ}\)
\(\iff \angle ECT=\angle ECB-\angle TCF\)
\(=70^{\circ}-34^{\circ}=36^{\circ}\cdots\)②
\(\triangle TBC \sim \triangle TEA \iff TE=TA\cdots\)③
また、\(\angle ETC=\angle ATB\cdots\)④
よって①③④より
\(\triangle ETC \equiv \triangle ATB\)
ゆえに②より
\( \iff \angle ECT=\angle ABT=36^{\circ}\)
Ⅲ (答) \(36^{\circ}\)