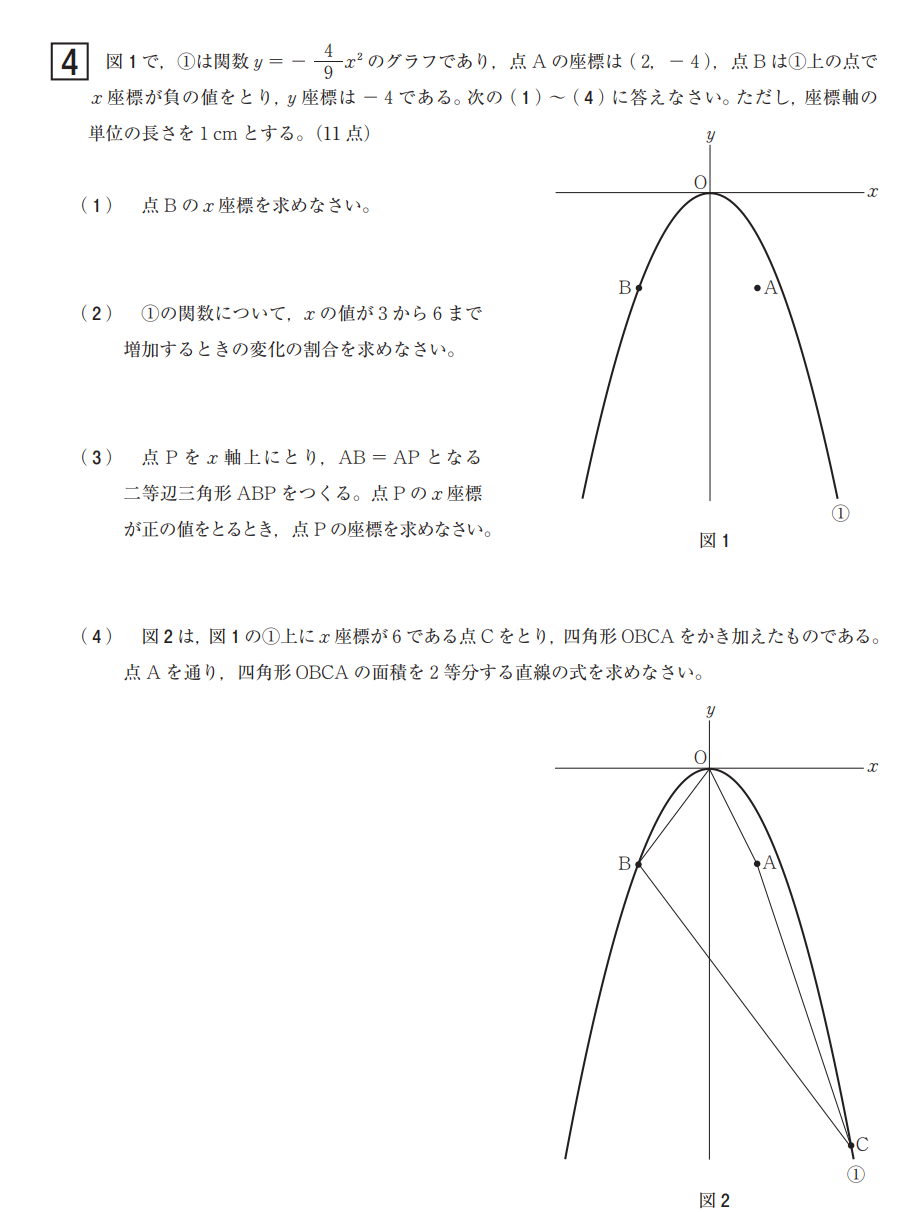
アクトイン代表：熊原 全体的に素直で解きやすい問題であるが、大問4⃣（４）の面積問題は頻出なので確認のために解答してみよう。
大問4⃣
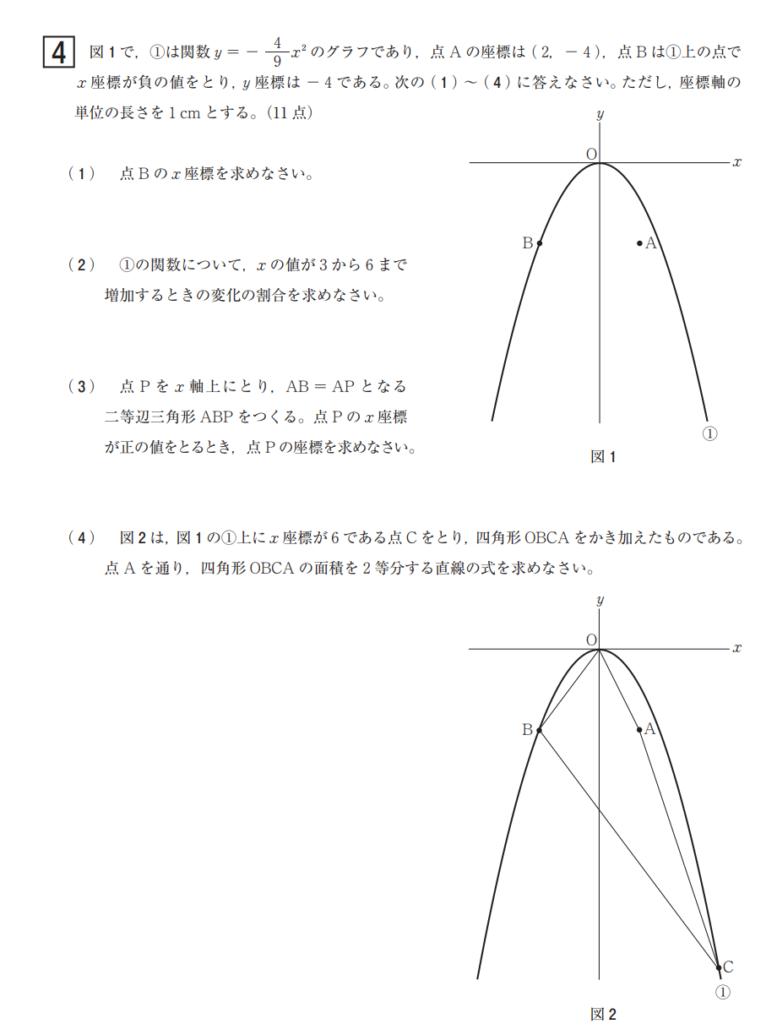
4⃣（４）解答例
\(B(-3,-4), \ A(2,-4)\)
点\(C\)の\(x\)座標は\(6\)であるから、点\(C\)の\(y\)座標は
\(y=-\frac{4}{9} \times 6^2=-16\)
\(C(6,-16)\)
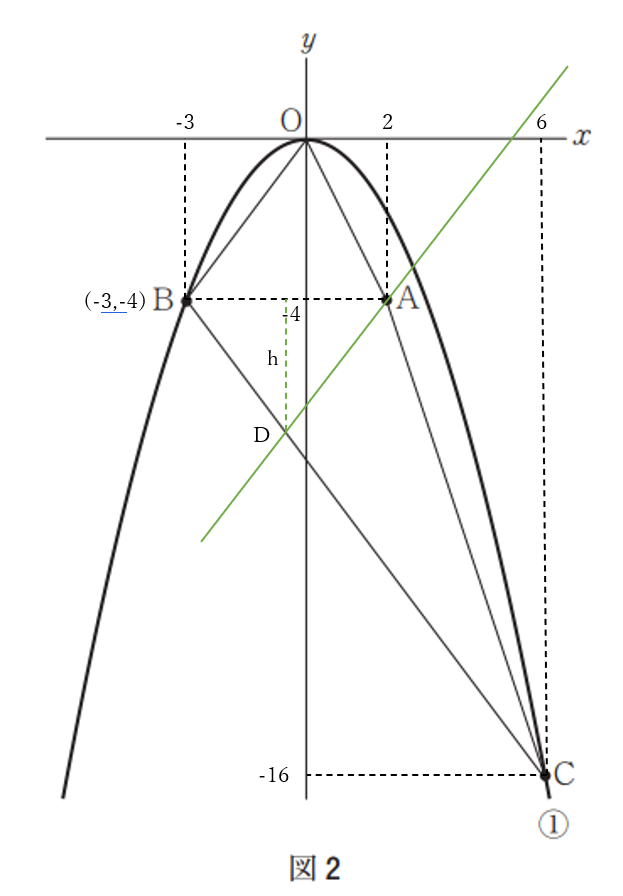
四角形\(OBCA\)の面積は、
\(\triangle OBA + \triangle BCA\)
\( =\frac{1}{2}AB \times 4 +\frac{1}{2}AB \times 12\)
\(=\frac{1}{2} \times 5 \times 4 + \frac{1}{2} \times 5 \times 12\)
\(=10+30=40\)
\(\triangle OBA=10, \ \triangle BCA=30\)だから、求める直線と線分\(BC\)は交わる。その交点を\(D\)とする。
\(\triangle ABD\)の面積が10になれば良いから、右の図のように、\(\triangle ABD\)の高さを\(h\)とすると
\(\frac{1}{2} \times AB \times h=10\)
\(\iff \frac{5}{2} \times h=10\)
\(\iff h=4\)
したがって、点\(D\)の\(y\)座標は\(-8\)である。
ここで、線分\(BC\)の方程式は $$ y=-\frac{4}{3}x-8 $$ よって、点\(D\)は\(y\)軸上にあり、\(D(0,-8)\)
したがって、求める直線の方程式は $$ y=2x-8 $$ である。
（答） \(y=2x-8\)