全体的に解きやすい問題が多い。大問4⃣の最後の問題は、できるだけ式を簡略化してから\(t\)で表すと計算しやすい。
大問4⃣

3解答例
(1)
\(A(t,2t^2), \ B(t+1,2(t+1)^2)\)
\(C(t+2,2(t+2)^2)\)
(1)(答) \(2(t+2)^2\)
(2)
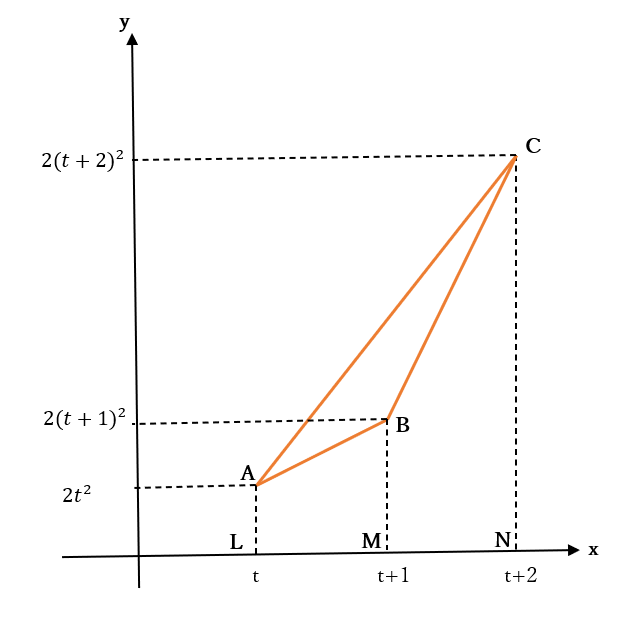
右の図のように、
\(A\)からおろした垂線の足を\(L\)
\(B\)からおろした垂線の足を\(M\)
\(C\)からおろした垂線の足を\(N\)
とする
\(\triangle ABC\)
\(=\)台形\(ALNC\)
\(-\)台形\(ALMB\)
\(-\)台形\(BMNC\)
\(=(AL+CN)\times 2\times \frac{1}{2}\)
\(-(AL+BM) \times \frac{1}{2}\)
\(-(BM+CN) \times \frac{1}{2}\)
\(=\frac{1}{2}(AL+CN)-BM\)
\(=\frac{1}{2} \{2t^2+2(t+2)^2\}-2(t+1)^2\)
\(=t^2+(t+2)^2-2(t+1)^2\)
\(=2\)
ゆえに、同じ面積になる
(2)(答) 同じ面積になる
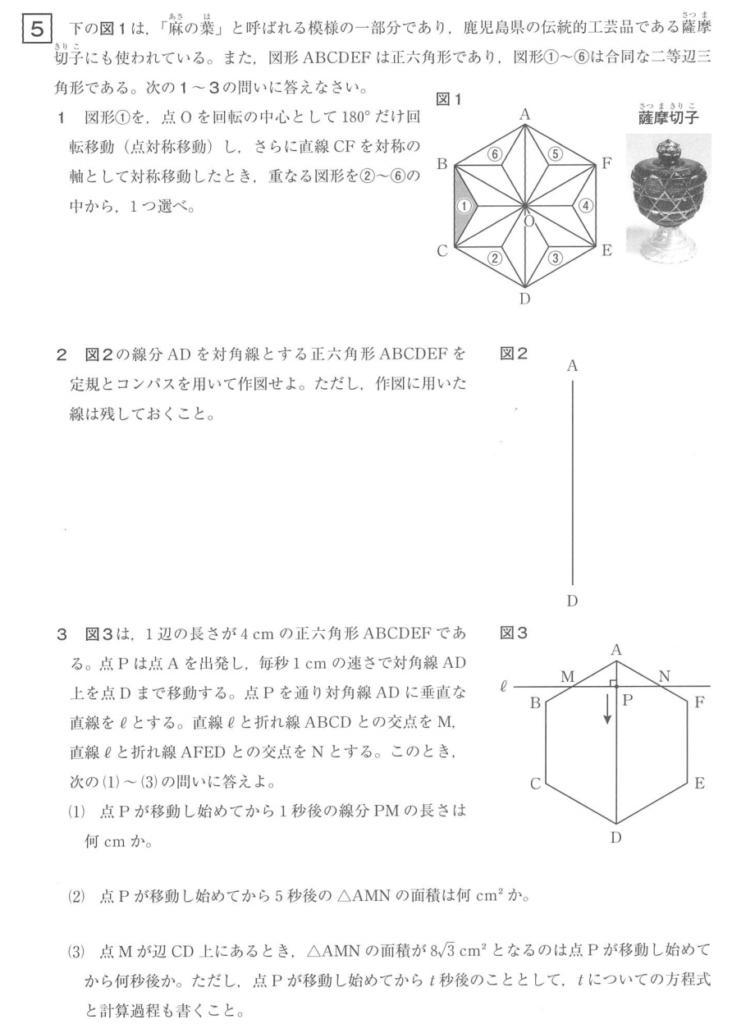
大問5⃣
(2)解答例
5秒後
\(AP=5, \ MP=2\sqrt{3}\)
\(\iff \triangle AMN=4\sqrt{3}\cdot 5\cdot \frac{1}{2}\)
\(=10\sqrt{3}\)
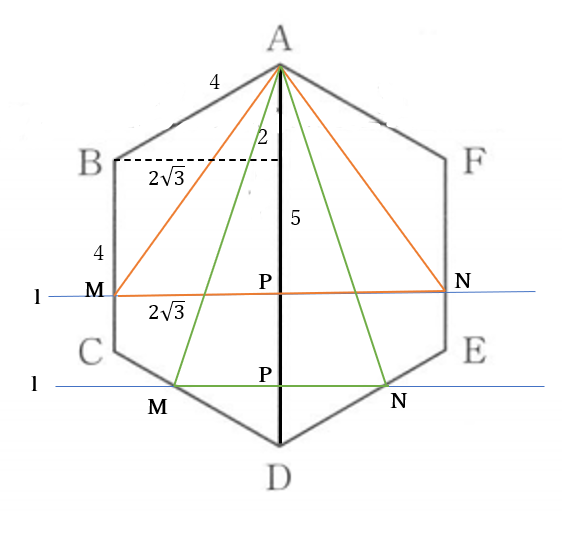
(2)(答) \(10\sqrt{3}\) \((cm^2)\)
(3)解答例
題意より
\(6 \leq t \leq 8\)
\(PD=8-t \iff MP=(8-t)\sqrt{3}\)
よって
\(\triangle AMN=2(8-t)\sqrt{3}\cdot t \cdot \frac{1}{2}\)
\(=t(8-t)\sqrt{3}\)
よって
\(t(8-t)\sqrt{3}=8\sqrt{3}\)
\(\iff t^2-8t+8=0\)
\(\iff t=4 \pm 2\sqrt{2}\)
\(6 \leq t \leq 8\)だから
\(t=4+2\sqrt{2}\)
(3)(答) \(4+2\sqrt{2}\) 秒後

