高校入試対策
暗算でサクサク解ける図形問題を集めています。出版用のブログなので、問題番号はその都度変えています。
問題は、ときどき継ぎ足していきます。
目標、50題
よく見かける有名な問題です。入試にも、ときどき出題されています。知っていればすぐに解ける問題ですが、解法をしっかり覚えましょう。
問題5
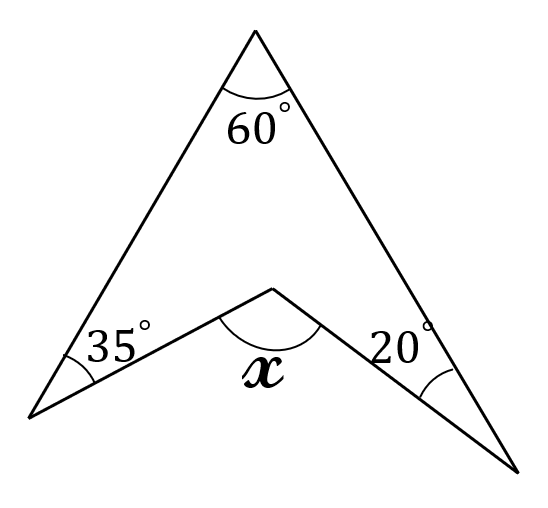
見ての通り、角度\( \ x \ \)を求めてください。
解答
(答) \(\large 115^{\circ}\)
三つの角度を足せばよいのです。知っている人は多いと思いますが、考え方(補助線を引く)が大切です。
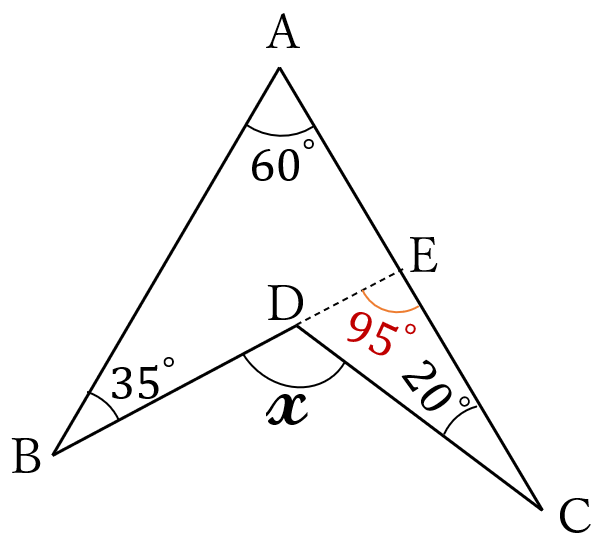
右の図のように、
線分\(BD \ \)の延長線と
線分\(AC \ \)との交点を
\(E \ \)とします。
右図より
\(\angle BEC=35^{\circ} + 60^{\circ}=95^{\circ}\)
よって、\(x=95^{\circ} + 20^{\circ}=115^{\circ}\)
結局、 \(x=35^{\circ}+20^{\circ}+60^{\circ}=115^{\circ}\) となります。
似たような問題が入試によく出ています。
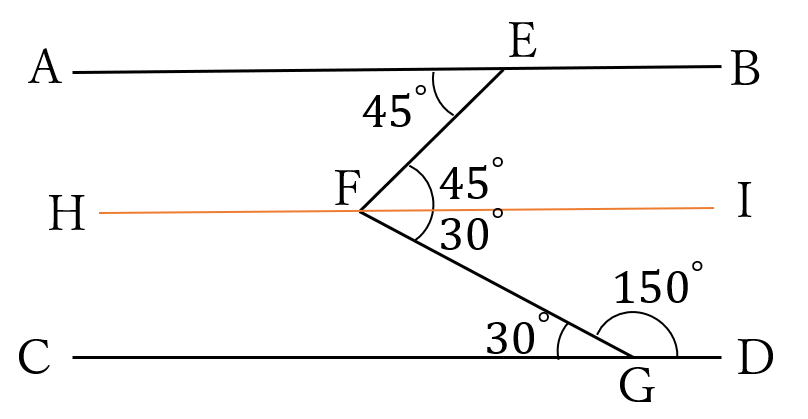
問題2
\(AB//CD \ \)です。角度\(x \ \)を求めてください。
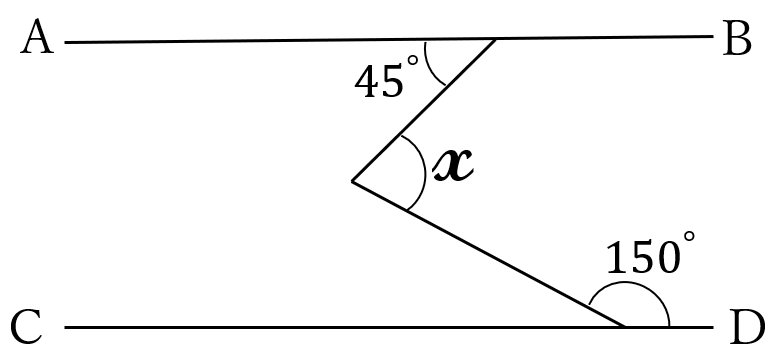
解答
(答) \(\large 75^{\circ}\)
図のように、直線\(EF \ \)の延長線と直線\(CD \ \)との交点を\(H \ \)とします。
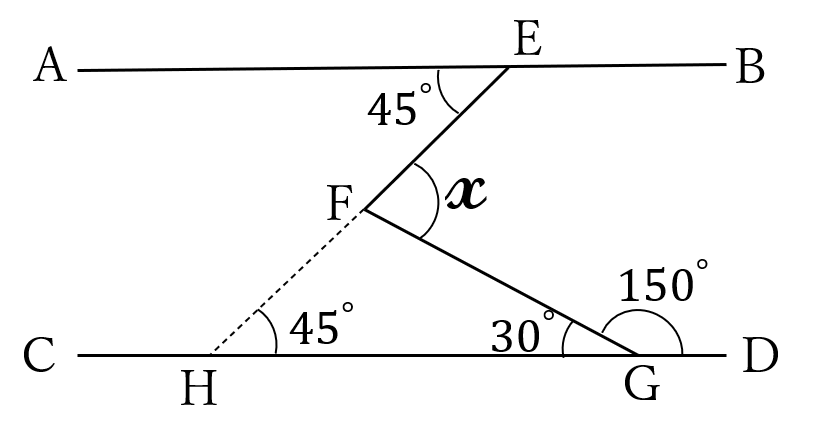
\(\angle AEH=\angle GHF=45^{\circ}\)(錯角)、\(\angle FGH=30^{\circ}\)
\(x=45^{\circ}+30^{\circ}=75^{\circ}\)
別解
補助線の引き方はいろいろです。
図のように、直線\(AB, \ CD \ \)に平行で、点\(F \ \)を通る直線\(HI \ \)を引く方法もあります。
問題10
下の図で、\(\angle x \ \)の大きさを求めてください。
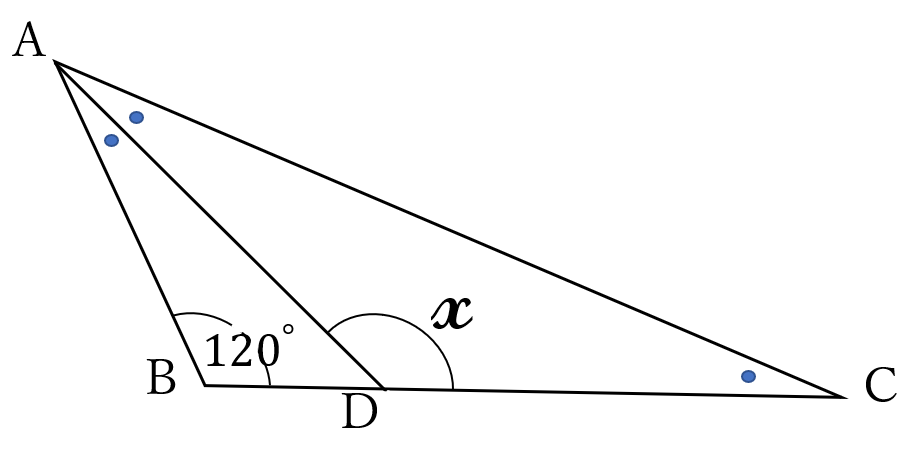
線分\(AD \ \)は\(\angle BAC \ \)を二等分してます。
\(\angle DAC =\angle DCA, \ \angle ABC =120^{\circ} \ \)です。
解答
(答) \(\large 140^{\circ}\)
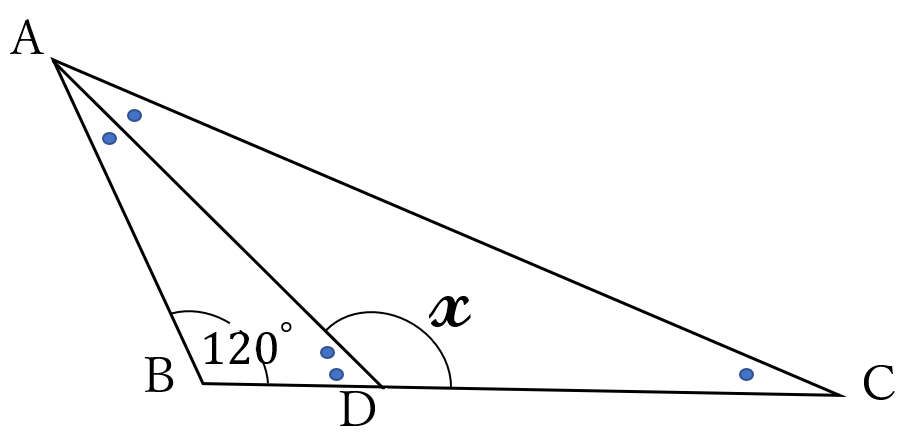
\(\angle BAD = a \ \)とおくと、
\(\angle DAC =\angle DCA = a \ \)だから、
\(\angle ABC + \angle BAC + \angle BCA = 120^{\circ} +3a=180^{\circ}\)
\(3a=180^{\circ}-120^{\circ}=60^{\circ}, \ a=20^{\circ}\)
\(\angle ADB =2a=40^{\circ}\) よって、
\(x=180^{\circ}-40^{\circ}=140^{\circ}\)
円周角と中心角の基本問題ですが、円周角が\(90^{\circ} \ \)よりも大きくなると、ちょっと戸惑います。
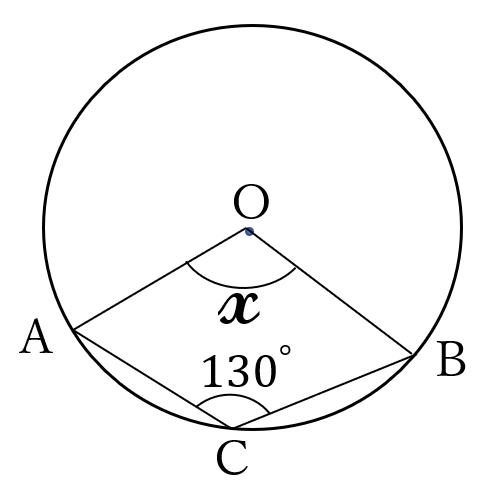
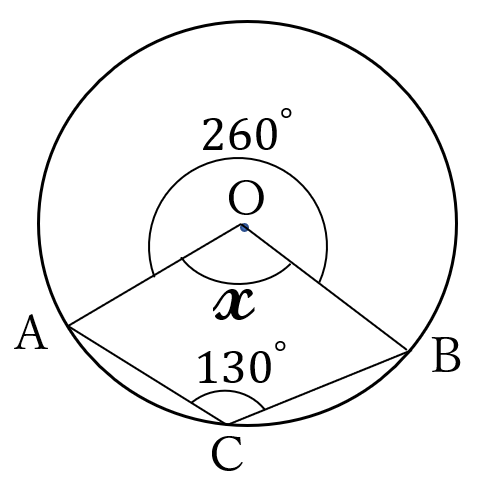
問題11
円\(O \ \)の円周上に、点\(A,B,C \ \)があります。円\(O \ \)の中心を\(O \ \)とします。
\(\angle ACB=130^{\circ} \ \)のとき、図の\(\large x \ \)\((\angle AOB) \ \)の大きさを求めてください。
解答
(答) \(\Large 100^{\circ}\)
円周角\(\angle ACB \ \)に対する中心角は\(\angle AOB \ \)の大きい方です。
したがって、
\(x=360^{\circ}-130^{\circ}\times 2\)\(\large =100^{\circ}\)
問題12
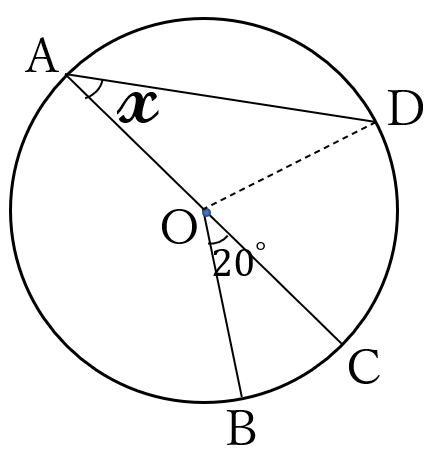
図のように、円\(O \ \)の円周上に4つの点
\(A, \ B, \ C, \ D\)
があり、
線分\(AC \ \)は円の直径
です。
\(\angle BOC=20^{\circ} \ \)で、\(\stackrel{\huge\frown}{CD}\)の長さが\(\stackrel{\huge\frown}{BC}\)の長さの\(3 \ \)倍であるとき、\(\angle x\)の大きさを求めなさい。
ただし、\(\stackrel{\huge\frown}{BC}, \ \stackrel{\huge\frown}{CD}\)は、いずれも小さいほうの弧とします。
解答
(答) \(\Large 30^{\circ}\)
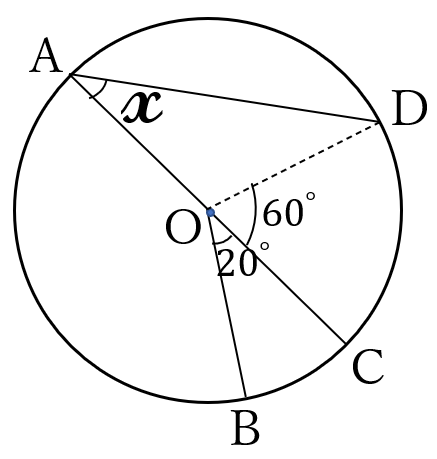
中心角、円周角の大きさは弧の長さに比例します。
弧の長さが\(n \ \)倍されると、中心角、円周角も\(n \ \)倍になります。
\(\Large x=\frac{1}{2} \angle COD =\frac{1}{2} \angle BOC\times \frac{\stackrel{\huge\frown}{CD}}{\stackrel{\huge\frown}{BC}}\)
\(\Large =\frac{1}{2} \times 20^{\circ} \times 3=30^{\circ}\)
問題46
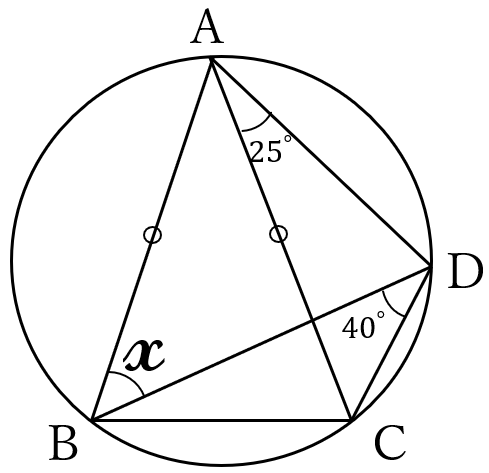
図のように、
円の周上に
3点\(A, \ B, \ C \ \)
があります。
\(\triangle ABC \ \)は
\(AB=AC \ \)の
二等辺三角形
です。
点\(B \ \)を含まない
方の\(\stackrel{\huge\frown}{AC} \ \)上に
点\(D \ \)をとり、
点\(A \ \)と点\(D \ \)、
点\(B \ \)と点\(D \ \)、点\(C \ \)と点\(D \ \)を結びます。
\(\angle BDC=40^{\circ}, \ \angle CAD=25^{\circ} \ \) のとき、
\(x\)\((\angle ABD)\) の大きさを求めなさい。
解答
(答) \(\large 45^{\circ}\)
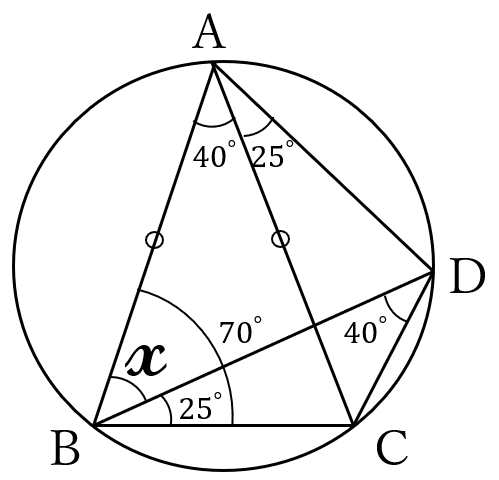
\(\stackrel{\huge\frown}{BC}\)に対する円周角は
等しいから、
\(\angle BDC = \angle BAC\)
\(=40^{\circ}\)
さらに、\(\triangle ABC \ \)は
\(AB=AC\)
の二等辺三角形だから
\(\angle ABC = \angle ACB\)
より、
\(\angle ABC =\frac{180^{\circ}-40^{\circ}}{2}\)
\(=70^{\circ}\)
\(\stackrel{\huge\frown}{CD}\)に対する円周角より、\(\angle DAC = \angle DBC =25^{\circ}\)
だから
\(\angle ABD =\angle ABC – \angle DBC=70^{\circ}-25^{\circ}=45^{\circ}\)
前問の続きです。
問題47
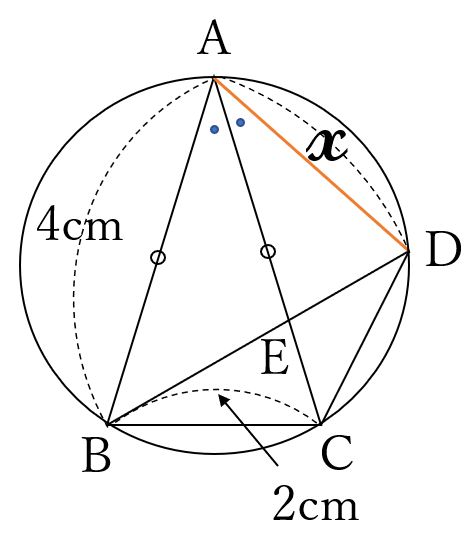
図のように、
円の周上に
3点\(A, \ B, \ C \ \)
があります。
\(\triangle ABC \ \)は
\(AB=AC \ \)の
二等辺三角形です。
点\(B \ \)を含まない方の
\(\stackrel{\huge\frown}{AC} \ \)上に
点\(D \ \)をとり、
点\(A \ \)と点\(D \ \)、
点\(B \ \)と点\(D \ \)、点\(C \ \)と点\(D \ \)を結び、線分\(AC \ \)と線分\(BD \ \)との交点を\(E \ \)とします。
\(\angle BAC = \angle CAD, \ AB=4cm, \ BC=2cm \ \)
のとき、線分\(AD \ \)の長さを求めてください。
解答
(答) \(\large 3\) \((cm)\)
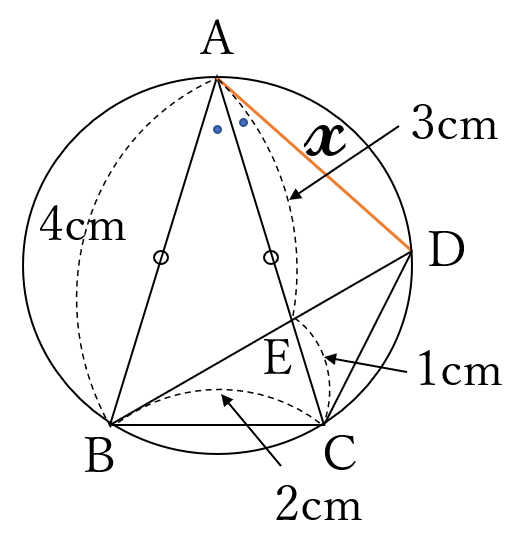
\(\triangle ABC\)と\(\triangle BCE\)
において、仮定と、
\(\stackrel{\huge\frown}{CD}\)に対する円周角より
\(\angle BAC = \angle DAC \)
\(=\angle EBC\)
\(\angle ACB \ \)は共通
\(\angle BEC = \angle AED\)
(対頂角)
よって、
\(\triangle ABC \ \)∽\( \ \triangle BCE\)
∽\( \ \triangle AED\) ゆえ
\(AB:BC=BC:CE=2:1\) したがって \( CE=\frac{1}{2}BC=\frac{1}{2}\times 2=1\) よって
\(AE=AC-CE=4-1=3\)
\(\triangle AED \ \)は二等辺三角形だから\( \ AD=AE=3\)
問題31
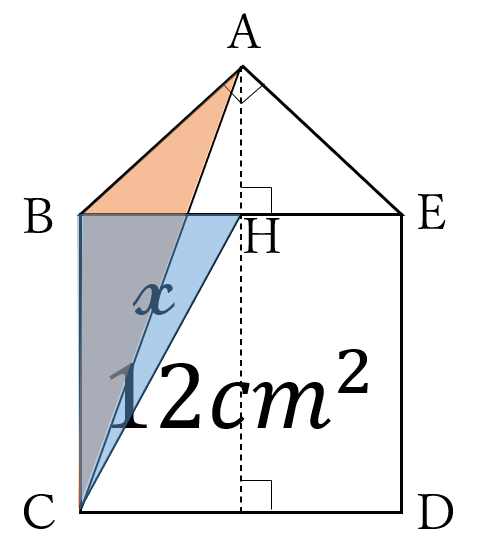
下の図のように、五角形\(ABCDE \ \)において、四角形\(BCDE\)は正方形で面積は\(12 \ cm^2 \ \)です。
\(\triangle ABE \ \)は、\(AB=AE, \ \angle BAE=90^{\circ} \ \)の直角二等辺三角形です。
\(\triangle ABC\)の面積を求めてください。
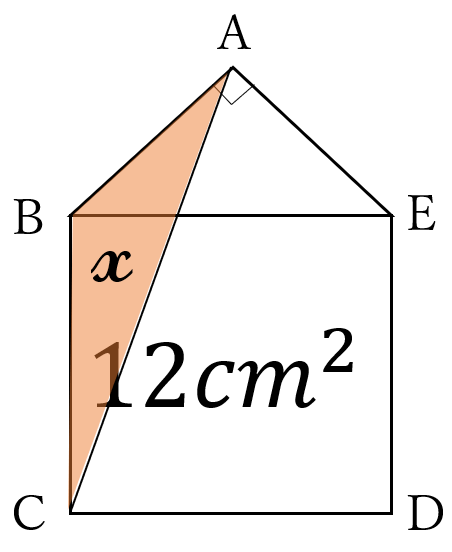
解答
(答) \(\Large 3\) \((cm^2)\)
下図の通りです。
\(\triangle ABC =\triangle BCH=12 \times \)\(\large \frac{1}{4}=3\)
問題32
右下の図のように、\(\angle BAC=90^{\circ} \ \)の直角三角形\(ABC \ \)があり、辺\(AB \ \)を1辺にもつ正方形\(ABDE \ \)と、辺\(BC \ \)を1辺にもつ正方形\(BCFG \ \)を、それぞれ直角三角形\(ABC \ \)の外側につくります。また、点\(D \ \)と点\(G \ \)を結びます。
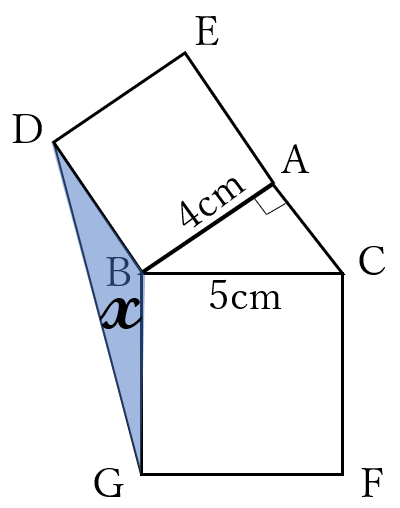
\(AB=4 \ cm\)
\(BC=5 \ cm\)
のとき、
\(\triangle BDG \ \)の面積を
求めてください。
解答
(答) \(\large 6\) \((cm^2)\)
右下の図、\(\triangle ABH \ \)と\( \ \triangle DBH’\)において、
\(\triangle ABH \equiv \triangle DBH’\)(証明略)\( \ \cdots \ (\ast)\) です。
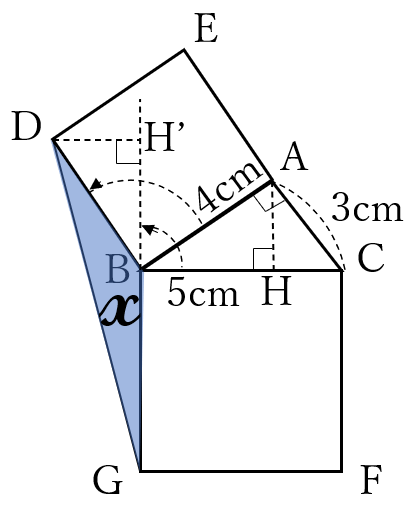
よって、\(DH’=AH \ \) より
\(\triangle BDG \ \)の面積と\(\triangle ABC \ \)
の面積は等しいです。
ここで、\(\triangle ABC \ \)は、
\(3:4:5 \ \)の直角三角形ゆえ
\(AC=3 \ cm\) よって
\(\triangle BDG =\triangle ABC\)
\(=AB\cdot AC \times \frac{1}{2}\)
\(=4 \times 3\times \frac{1}{2}=6\)
\((\ast)\) \(\triangle ABH \ \)を点\(B \ \)を
中心に反時計回りに\(90^{\circ} \ \)
回転させると、\(\triangle DBH’ \ \)にピッタリ重なります。
問題37
下の図のように、関数\( \ y=x^2 \ \)の
グラフ上に2点\(A(-1,1), \ B(2,4) \ \)があり、
直線\(AB \ \)の方程式は、\(y=x+2 \ \)です。
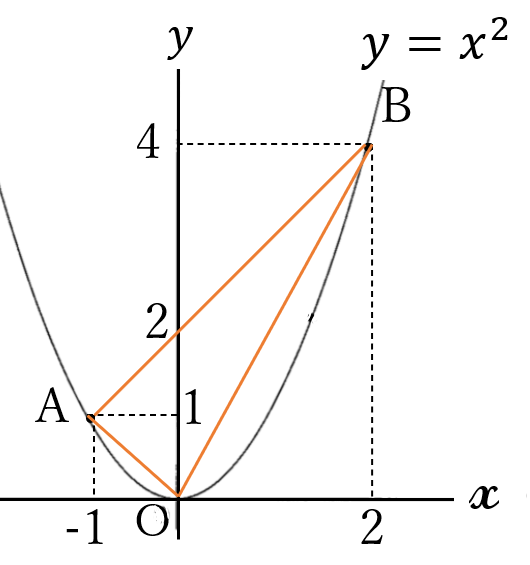
\(\triangle AOB \ \)の面積を求めてください。
解答
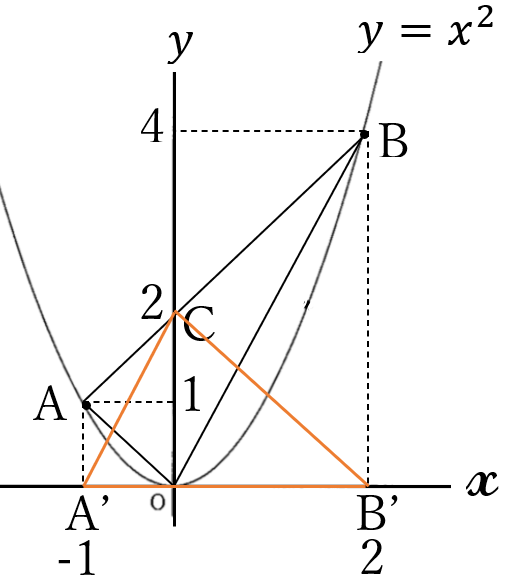
(答) \(\Large 3\)
\(\triangle AOB\)の面積は、
右図の\(\triangle CA’B’\)の
面積に等しいです。
\(\triangle AOB=\triangle AOC + \triangle COB \)
\(=\triangle CA’O + \triangle CB’O=\triangle CA’B’\)
\(=A’B’\cdot OC \times \frac{1}{2}=3\times 2 \times \frac{1}{2}=3\)
入試問題では、
点\(A,B\)の座標⇒直線\(AB\)の方程式⇒\(\triangle AOB\)の面積
の順で出題されることが多いです。
問題38
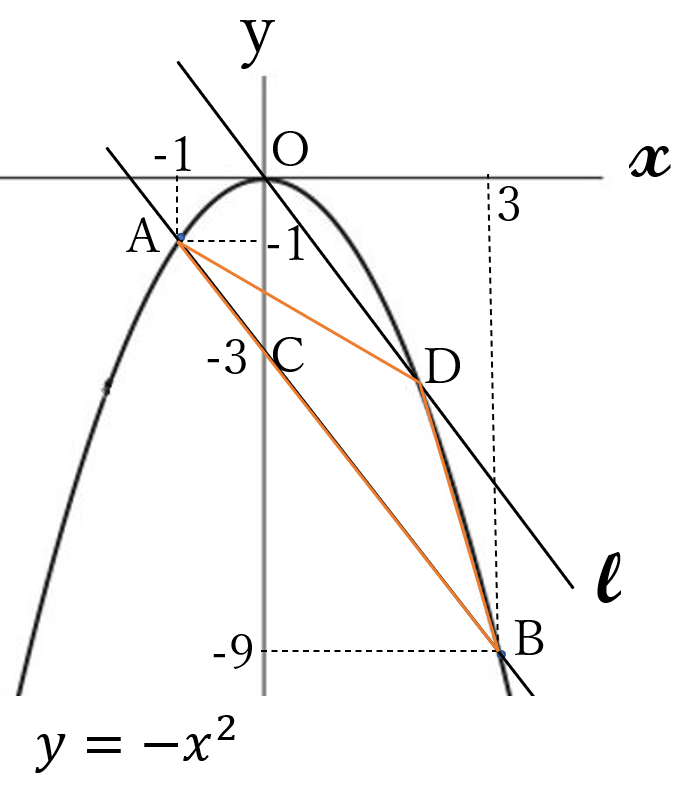
右の図のように
2次関数\( \ y=-x^2\)
のグラフ上に2点
\(A(-1,-1)\)
\(B(3,-9)\)
があります。
2点\(A, \ B\)
を通る直線
\(y=-2x-3 \ \)に平行で原点\(O \ \)を通る直線\( \ l \ \)と
\(y=-x^2 \ \)との交点を\(D \ \)とします。
\(\triangle ADB \)の面積を求めてください。
解答
(答) \(\Large 6\)
\(l//AB \ \)より\( \ \triangle ADB = \triangle AOB\)
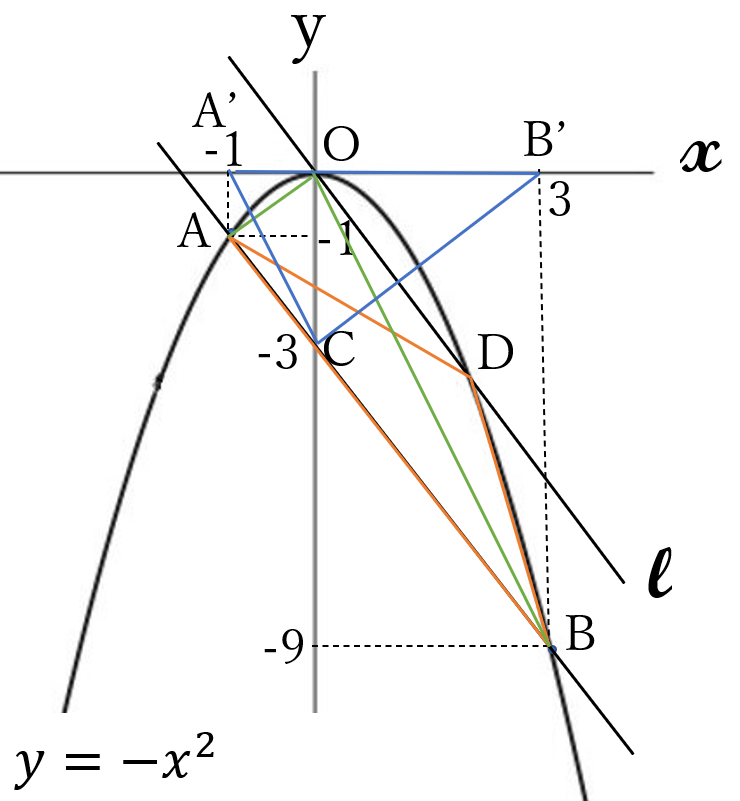
このことに気がつけば前問と同様にすぐに計算できます。
\(\triangle ADB =\triangle AOB =\triangle CA’B’\)
\(=A’B’\cdot OC \times \frac{1}{2} =4\times 3 \times \frac{1}{2}=6\)
問題39
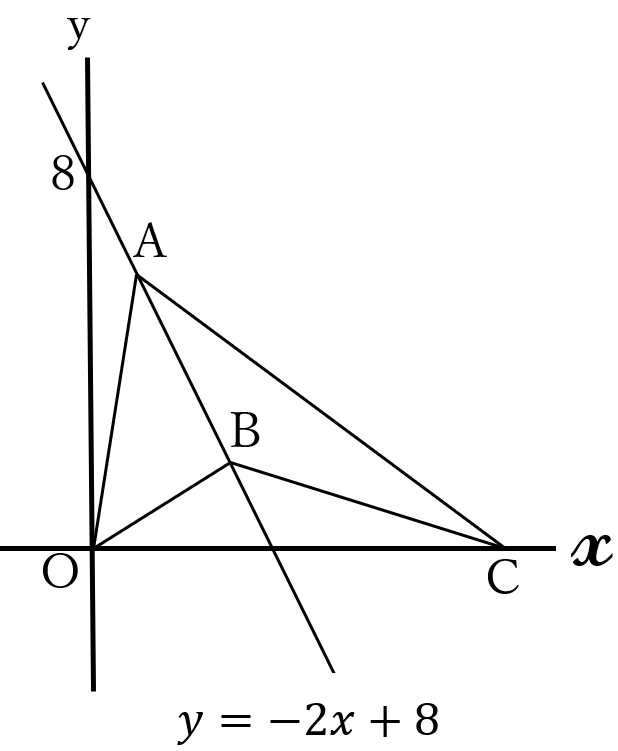
2点\(A, \ B \ \)は、
直線\( \ y=-2x+8 \ \)
上にあり、\(x \ \)座標は
それぞれ\( \ 1, \ 3 \ \)です。
点\(C \ \)は、\(x \ \)軸上
の点で、\(x \ \)座標は
正です。
\(\triangle AOB \ \)の面積と
\(\triangle ABC \ \)の面積が
等しいとき、点\(C \ \)
の座標を求めなさい。
解答
(答) \(\large C(8, \ 0)\)
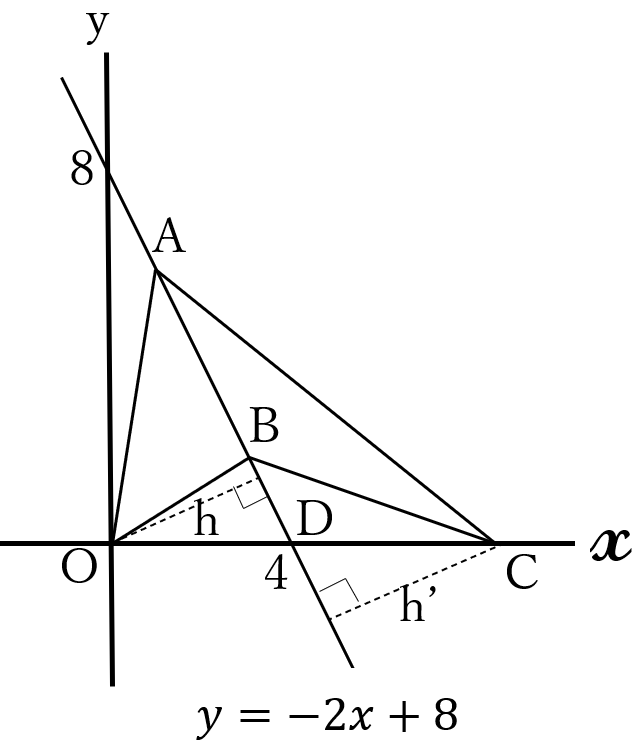
直線\( \ AB \ \)と\( \ x \ \)軸との
交点を\( \ D \ \)とおき
ます。 \(D(4,0)\)
\(\triangle AOB \ \)と\( \ \triangle ABC \ \)
の底辺を\( \ AB\)
とすると、
高さは等しいので、
右図において、
\(h=h’ \ \)です。
したがって、
\(\triangle AOD \ \)と\( \ \triangle ADC\)
の面積も等しいので
点\( \ D \ \)は、線分\( \ OC \ \)
の中点となり、\(C(8,0) \ \)です。
入試問題では、ある関数のグラフ上の2点\(A,B\)を通る直線の方程式を求めさせてからの問題になるでしょう。
前問の類題です。
問題40
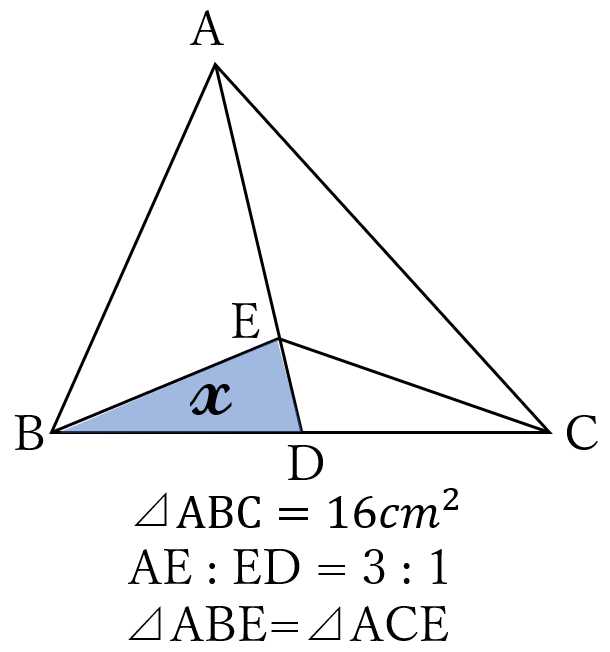
図のような\(\triangle ABC\)があり、\(\triangle ABC\)の面積は\(16cm^2\)です。辺\(BC\)上に点\(D\)があり、点\(A\)と点\(D\)を結びます。線分\(AD\)上に点\(E\)があり、\(AE:ED=3:1\)です。\(\triangle ABE\)と\(\triangle ACE\)の面積が等しいとき、\(\triangle EBD\)の面積\(\large x\)を求めなさい。
解答
(答) \(\large 2cm^2\)
\(\triangle ABE = \triangle ACE\)
より、
\(\triangle ABD =\triangle ACD\)
よって、
\(\Large x\)\((\triangle EBD)\)
\(=\triangle ABC \times \)\(\large \frac{1}{2} \times \)\(\large \frac{ED}{AD}\)
\(=16\times \)\(\large \frac{1}{2} \times \)\(\large \frac{1}{4}=2\)
問題27
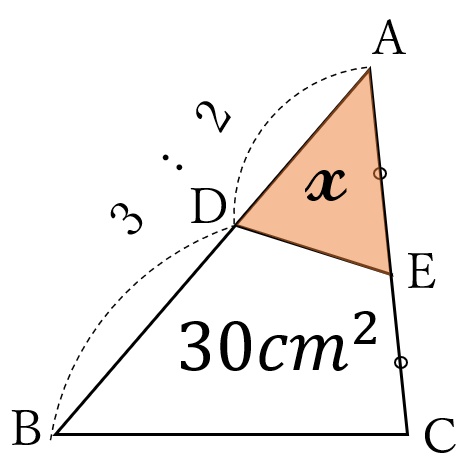
下の図のような\(\triangle ABC \ \)があり、面積は\( \ 30cm^2 \ \)です。
点\(D \ \)は辺\(AB \ \)上にあり、\(AD:DB=2:3 \ \)です。
点\(E \ \)は、辺\(AC \ \)の中点です。
\(\triangle ADE \ \)の面積\(\Large x \ \)を求めてください。
解答
(答) \(\Large 6 \) \((cm^2)\)
\(\Large x\)\((\triangle ADE)=\triangle ABC \times\)\(\large \frac{AE}{AC}\)\(\times\)\(\large \frac{AD}{AB}\)
\(=30\times\)\(\large \frac{1}{2}\)\( \times\)\(\large \frac{2}{5} =6\)

問題28
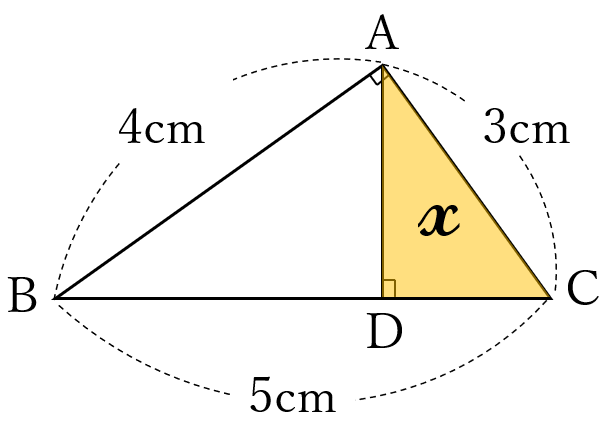
直角三角形\(ABC \ \)があります。
\(\angle BAC=90^{\circ}, \ AB=4 \ cm, \ AC=3 \ cm \ \)です。
\(A \ \)から辺\(BC \ \)に下した垂線と辺\(BC \ \)との交点を\(D \ \)とします。
\(\triangle ADC \ \)の面積\(\Large x \ \)を求めてください。
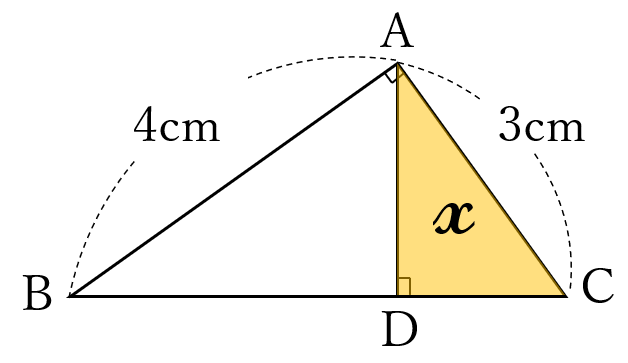
分数の計算になりますが、頑張って暗算で計算しましょう。
解答
(答) \(\Large \frac{54}{25}\) \((cm^2)\)
\(\triangle ABC\)は、\(3:4:5 \ \)の直角三角形だから、
\(BC=5 \ cm\)
\(\triangle ABC \ \)と\( \ \triangle DAC \ \)は相似で、相似比は\( \ BC:AC=5:3\)
\(\triangle ABC\)の面積は、\(3\times 4\times \frac{1}{2}=6 \ \)だから
\(\Large x\)\((\triangle ADC)=\triangle ABC \times \)\(\large (\frac{3}{5})^2\)\(=6\times \)\(\large \frac{9}{25} =\frac{54}{25}\)
問題29
平行四辺形\(ABCD \ \)において、辺\(DC \ \)上に、\(CE:ED=1:2 \ \)になるように点\(E \ \)をとり、線分\(AE \ \)と対角線\(BD \ \)との交点を\(F \ \)とします。
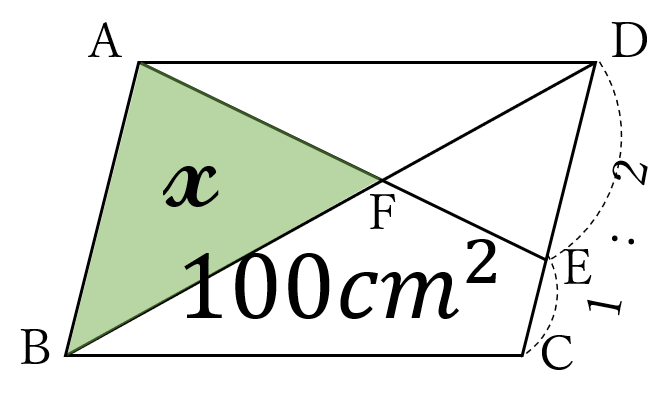
平行四辺形\(ABCD \ \)の面積が\(100 \ cm^2 \ \)のとき、
\(\triangle ABF\)の面積\(\large x\)を求めなさい。
解答
(答) \(\Large 30\) \((cm^2)\)
\(CE:ED=1:2 \ \)より、\(CD:ED=3:2\)
よって、\(AB=CD \ \)より、\(AB:ED=3:2\)
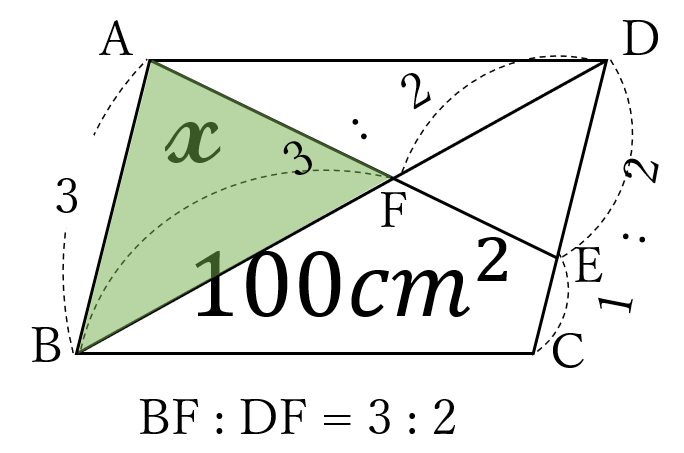
したがって、\(\triangle ABF \ \)∽\( \ \triangle EFD \ \)だから
\(BF:DF=3:2\) よって
\(\triangle ABF =\triangle ABD \times \)\(\large \frac{BF}{BD}\)
\(=平行四辺形ABCD \times \)\(\large \frac{1}{2}\)\( \times \)\(\large \frac{3}{5}\)\(=100\times \)\(\large \frac{1}{2}\)\( \times \)\(\large \frac{3}{5}=30\)
