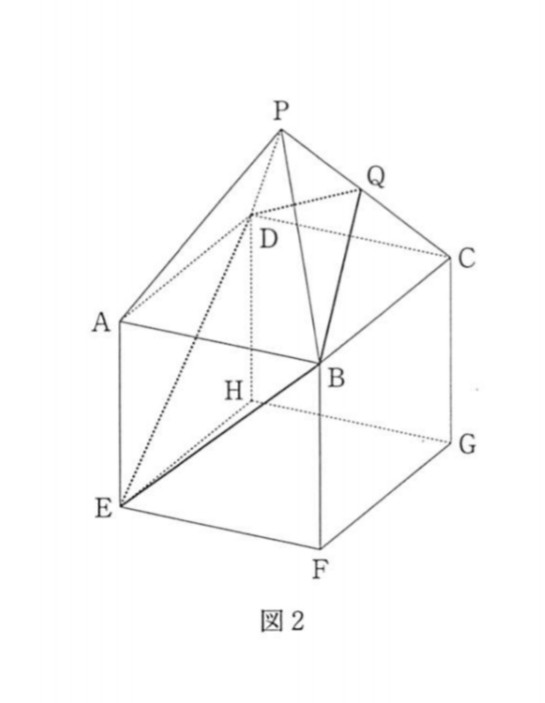
点数で差がつくと思われる問題は大問4と大問5と思われる。大問4については、他で解説しているので、ここでは大問5の解法について述べる。
問5の問題は下記のとおりです。問題用紙をコピーしてそのまま張り付けてあります。
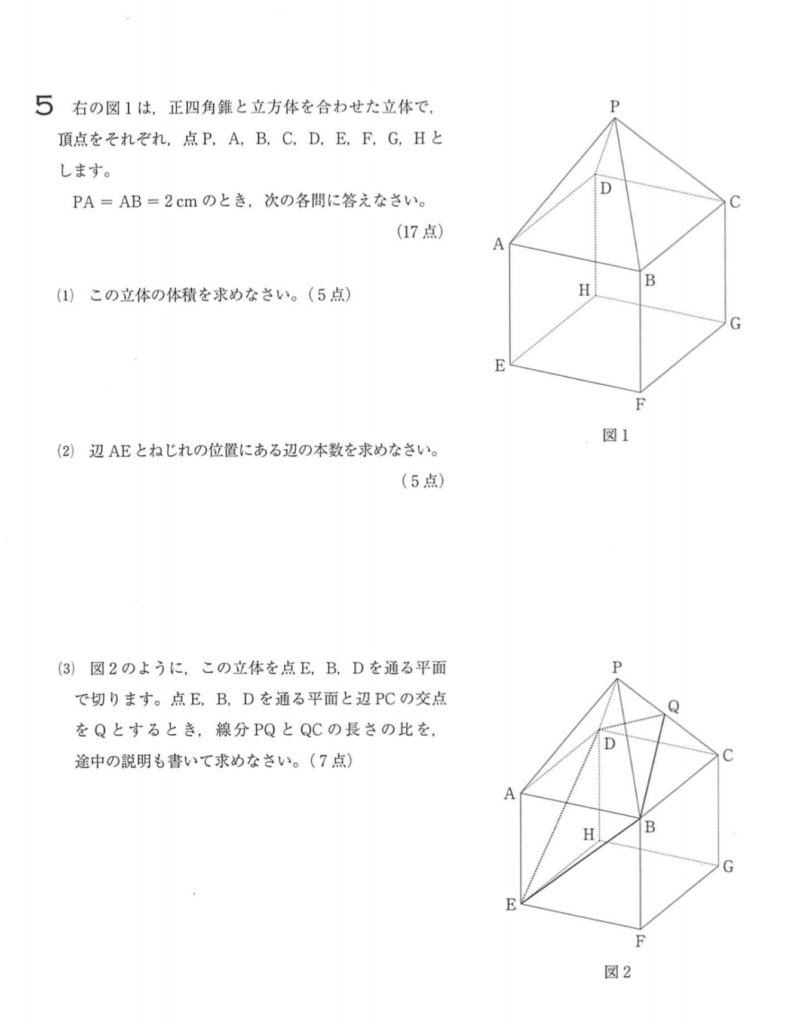
(1)、(2)は解きやすいと思うので、(3)を解答(解説)します。
県の解答はちょっと解りずらいです。県のHPに掲載されている解答を載せておきます。

まず、\(EQ\)の延長線と\(GC\)の延長線の交点をとる必要はありません。また、この二つの延長線が交わることの説明を省略しています。
さらに、最終的な解答が \(\sqrt{2}:2\) となっていますが、\(1:\sqrt{2}\) のほうが「すっきり」しています。
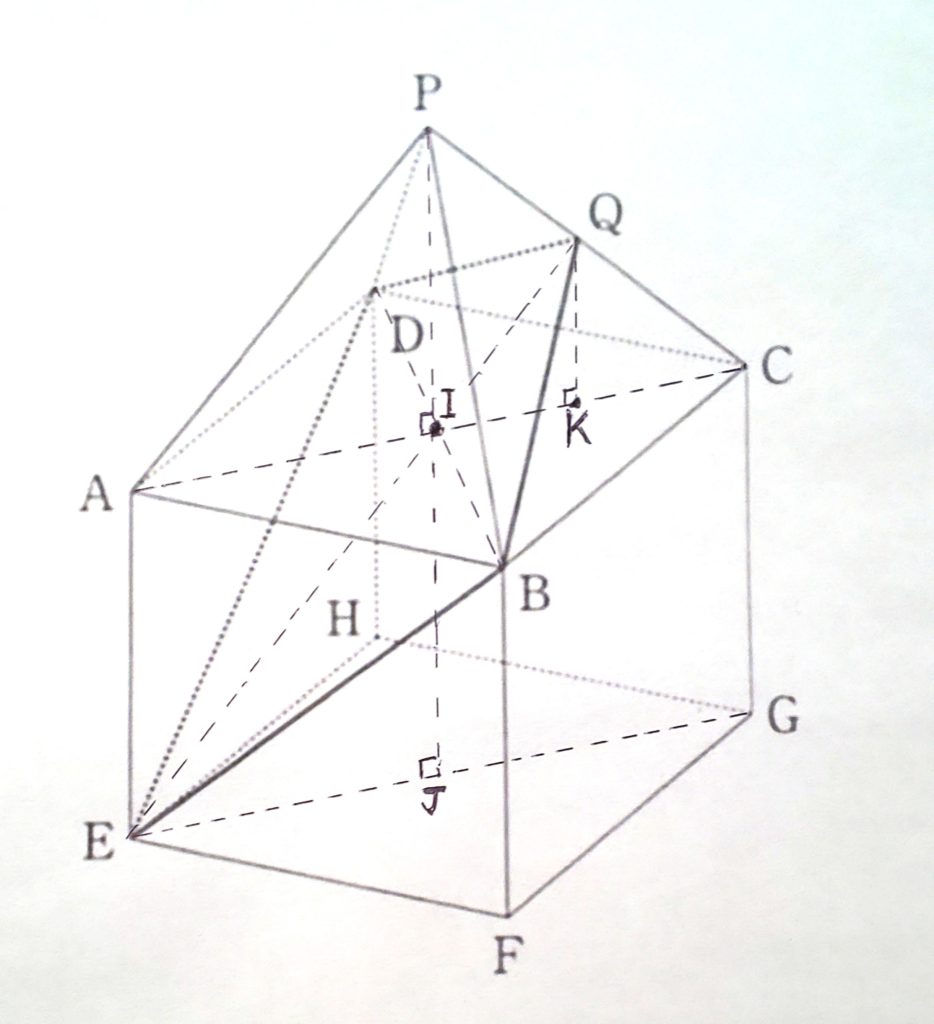
では、私なりの解答(解説)を載せておきます。
四角形\(DEBQ\)において
\(ED=EB\) , \(QD=QB\) だから、
対角線 \(EQ\) は\(BD\) の中点で交わっている。
この中点を \(I\) とおくと、\(I\) は \(AC\) の中点でもある。また、
頂点 \(P\) から四角形\(DABC\)に下した垂線の足も点 \(I\) である。
頂点 \(P\) から四角形\(HEFG\) に下した垂線の足を \(J\)、
点 \(Q\) から四角形\(DABC\) に下した垂線の足を \(K\) とする。
点 \(J\) は線分 \(EG\) 上に、点 \(K\) は線分 \(AC\) 上にある。
よって、点 \(P,A,E,G,C,Q,I,J,K\) は同一平面上にあり、
その図は右のようになる。
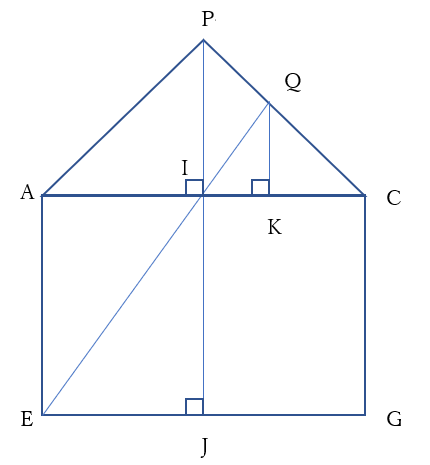
ここで \(EJ=\sqrt{2} , IJ=2\)
直角三角形\(IEJ\) と直角三角形\(QIK\) において
\(\angle IEJ=\angle QIK\)(同位角)、よって
\(\triangle IEJ \sim \triangle QIK\) また、
\(\triangle PIC\) は、\(PI=IC=\sqrt{2}\) の直角二等辺三角形で、
さらに \(\triangle PIC \sim \triangle QKC\) だから、\(QK=KC\)
以上より、
\(PQ:QC=IK:KC=IK:QK\)
\(=EJ:IJ=\sqrt{2}:2=1:\sqrt{2}\)
(答え \(PQ:QC=\))\(1:\sqrt{2}\)