それでは、例を参考にして、例題をやってみましょう。筆記用具が無くても大丈夫です。頂点と軸を求め、頭の中でグラフ(放物線)をイメージするだけで良いです。
例題1
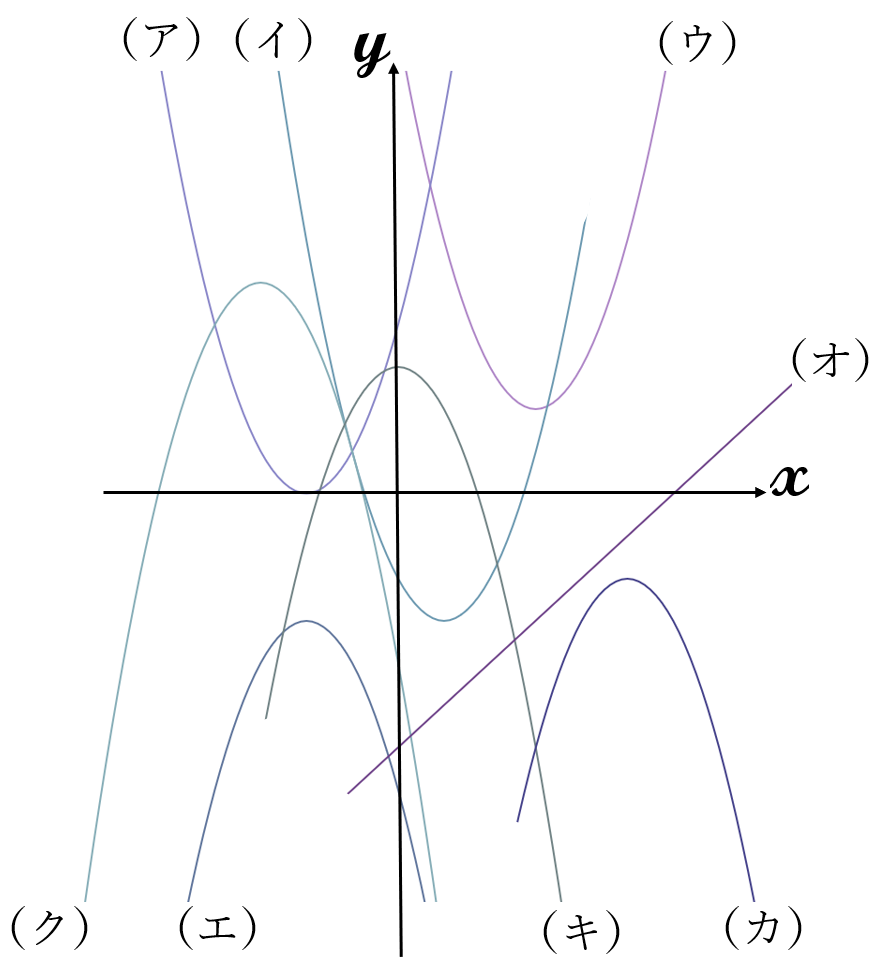
次の2次関数のグラフ(放物線)の頂点と軸を求め、そのグラフを図の(ア)~(ク)から選んで記号で答えなさい。
(1) \(\Large y=(x-3)^2+2\)
頂点( \(,\) )
軸
(2) \(\Large y=(x+2)^2\)

頂点( \(,\) )
軸
(3) \(\Large y=-(x+2)^2-3\)

頂点( \(,\) )
軸
(4) \(\Large y=(x-1)^2-3\)

頂点( \(,\) )
軸
(5) \(\Large y=-(x+3)^2+5\)

頂点( \(,\) )
軸
(6) \(\Large y=-x^2+3\)

頂点( \(,\) )
軸
解答
(1) \(\Large y=(x-3)^2+2\)

頂点\( \ (3, \ 2)\)
軸 \( \ x=3\)
下に凸
(ウ)
(2) \(\Large y=(x+2)^2\)

頂点\( \ (-2, \ 0)\)
軸 \( \ x=-2\)
下に凸
(ア)
(3) \(\Large y=-(x+2)^2-3\)

頂点\((-2,-3)\)
軸 \( \ x=-2\)
上に凸
(エ)
(4) \(\Large y=(x-1)^2-3\)

頂点\( \ (1,-3)\)
軸 \( \ x=1\)
下に凸
(イ)
(5) \(\Large y=-(x+3)^2+5\)

頂点\( \ (-3, \ 5)\)
軸 \( \ x=-3\)
上に凸
(ク)
(6) \(\Large y=-x^2+3\)

頂点\( \ (0, \ 3)\)
軸 \( \ x=0\)
(\(y \ \)軸)
上に凸
(キ)
第一段階の最終目標です。
2次関数のグラフの描き方
次は、2次関数のグラフを描きます。
ポイントは3つあります。
1.頂点を記す
2.上に凸か下に凸か
3.頂点以外の点を1つ記す
では、例題をやってみましょう。
例題2
次の2次関数のグラフを描きなさい。
(1) \(\Large y=(x-2)^2+3\)
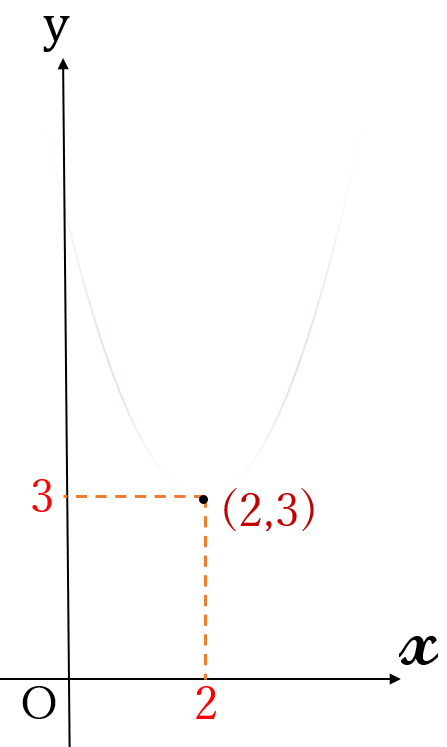
頂点\( \ (2, \ 3)\)
軸 \(x=2\) 下に凸
① まず、頂点を
点\(\bullet \ \)で記します。
大切なことは、頂点\(\bullet \ \)に座標を書き込むことです。頂点\(\bullet \ \)の近くに\( \ (2,3) \ \)と書いても良いですし、点線を引いて\(x\)座標に\(2\)、\(y\)座標に\(3\)と記しても良いです。これを省いてはいけません。
原点\( \ O \ \)も書き忘れてはいけません。書き忘れると減点される場合があります。 次ページに続く
(1) \(\Large y=(x-2)^2+3 \ \cdots (\ast)\)
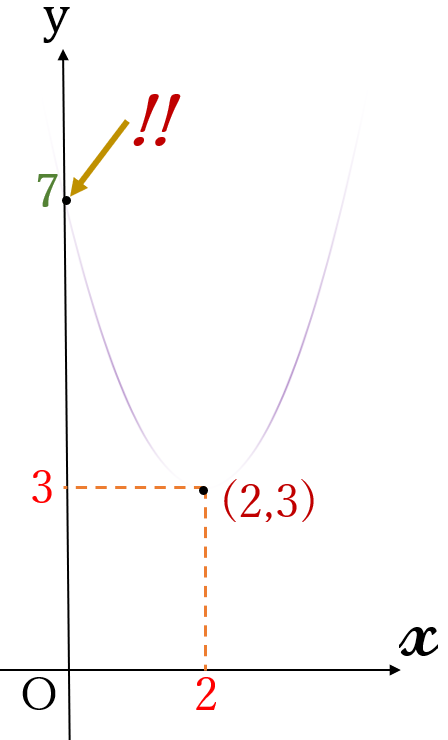
頂点\( \ (2, \ 3)\)
軸 \(x=2\)
下に凸
② 次に、\((\ast)\)の放物線と\(y\)軸との交点を求めます。
2次関数の式\((\ast)\)において\( \ x=0 \ \)のときの\(y\)の値が\(y\)軸との交点の\(y\)座標になります。
\(y=(x-2)^2+3\)
において、
\(x=0 \ \)のとき、
\(y=(0-2)^2+3=(-2)^2+3=4+3=7\)
\((\ast) \ \)の放物線と\( \ y \ \)軸との交点は\( \ (0, \ 7) \ \)となります。
点\( \ (0, \ 7) \ \)を記し、\(7\)と書き込みます。 次ページに続く
(1) \(\Large y=(x-2)^2+3\)
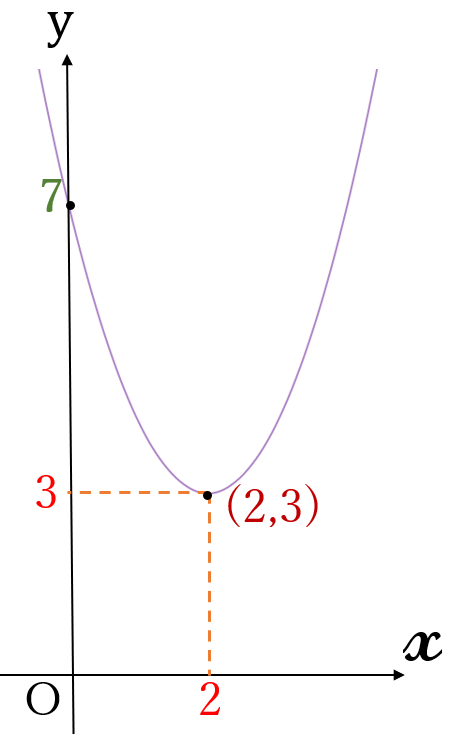
頂点\( \ (2, \ 3)\)
軸 \(x=2\)
下に凸
③ 頂点周辺から、下に凸の放物線を描きます。かならず、\(y\)軸との交点\( \ (0, \ 7) \ \)を通るように描きます。できるだけ滑らかに描きましょう。
後に、2次関数の決定で学習しますが、放物線は頂点と頂点以外の1つの点の座標が定まれば、放物線が決定されます。この頂点以外の1つの点を、\(y\)軸との交点にすると解りやすいです。
次の2次関数のグラフを描きなさい。
(2) \(\Large y=-\frac{1}{2}(x+2)^2+5\)
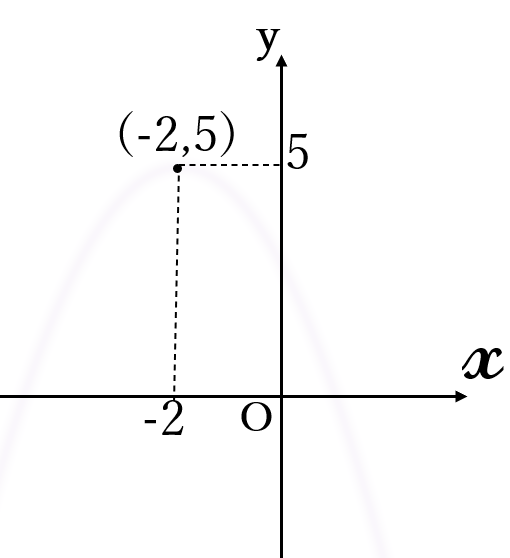
頂点\( \ (-2, \ 5)\)
軸 \(x=-2\)
上に凸
① まず、頂点を
点\(\bullet \ \)で記します。
大切なことは、頂点\(\bullet \ \)に座標を書き込むことです。頂点\(\bullet \ \)の近くに\( \ (-2,5) \ \)と書いても良いですし、点線を引いて\( \ x \ \)座標に\(-2\)、\(y \ \)座標に\(5\)と記しても良いです。これを省いてはいけません。
次ページに続く
(2) \(\Large y=-\frac{1}{2}(x+2)^2+5 \ \cdots \ (\ast)\)
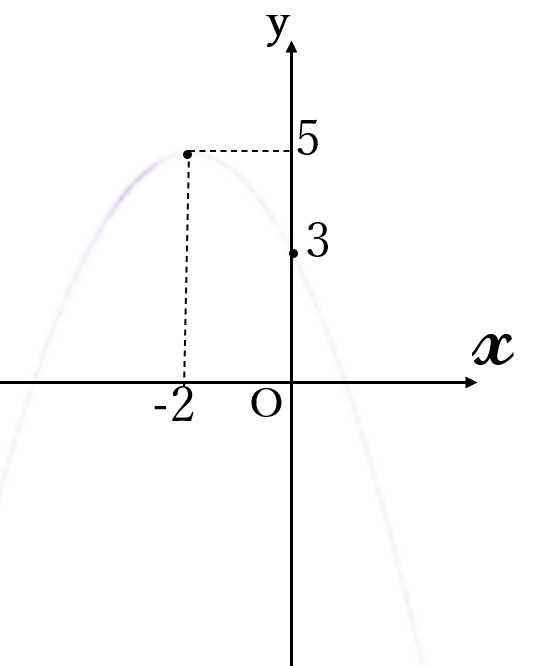
頂点\( \ (-2, \ 5)\)
軸 \(x=-2\)
上に凸
② 次に、\((\ast)\)の放物線と\( \ y \ \)軸との交点を求めます。
2次関数の式\((\ast)\)において\( \ x=0 \ \)のときの\( \ y \ \)の値が\( \ y \ \)軸との交点の\( \ y \ \)座標になります。
\(y=-\frac{1}{2}(x+2)^2+5 \ \)において、\(x=0 \ \)のとき、
\(y=-\frac{1}{2}(0+2)^2+5=-\frac{1}{2} \times 2^2+5=-2+5=3\)
\((\ast) \ \)の放物線と\( \ y \ \)軸との交点は\( \ (0, \ 3) \ \)となります。
点\( \ (0, \ 3) \ \)を記し、\(3\)と書き込みます。 次ページに続く
(2) \(\Large y=-\frac{1}{2}(x+2)^2+5\)
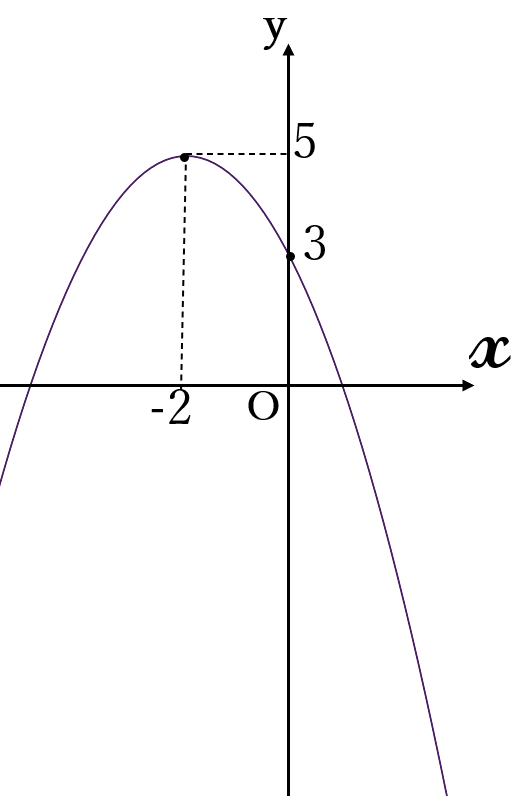
頂点\( \ (-2, \ 5)\)
軸 \(x=-2\)
上に凸
③ 頂点周辺から、下に凸の放物線を描きます。かならず、\( \ y \ \)軸との交点\( \ (0, \ 3) \ \)を通るように描きます。できるだけ滑らかに描きましょう。
後に、2次関数の決定で学習しますが、放物線は頂点と頂点以外の1つの点の座標が定まれば、放物線が決定されます。この頂点以外の1つの点を、\( \ y \ \)軸との交点にすると解りやすいです。
\(x\)軸と交わる場合には、\(x\)軸との交点を記しても良いですが、2次方程式を解くことになるので、計算が複雑になる場合があります。
次の2次関数のグラフを描きなさい。
(3) \(\Large y=2(x-3)^2+4\)
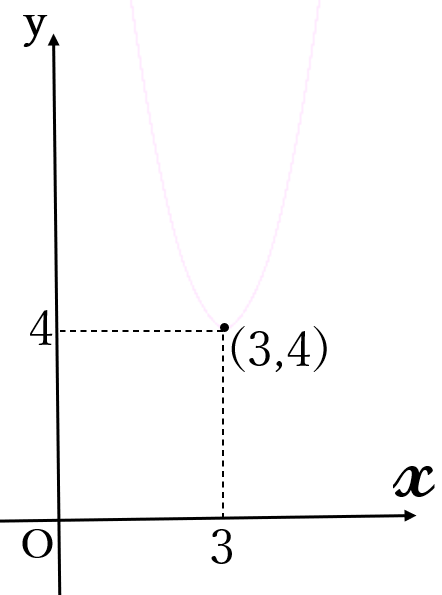
頂点\( \ (3, \ 4)\)
軸 \(x=3\)
下に凸
① まず、頂点を
点\(\bullet \ \)で記します。
大切なことは、頂点\(\bullet \ \)に座標を書き込むことです。頂点\(\bullet \ \)の近くに\( \ (3,4) \ \)と書いても良いですし、点線を引いて\(x\)座標に\(3\)、\(y\)座標に\(4\)と記しても良いです。これを省いてはいけません。
次ページに続く
(3) \(\Large y=2(x-3)^2+4 \ \cdots (\ast)\)
頂点\( \ (3, \ 4)\)
軸 \(x=3\)
下に凸
② 次に、\((\ast)\)の放物線と\(y\)軸との交点を求めます。
\((\ast)\)において、
\(x=4 \ \)のとき、
\(y=2(0-3)^2+4\)
\(=2 \times 3^2+4=22\)
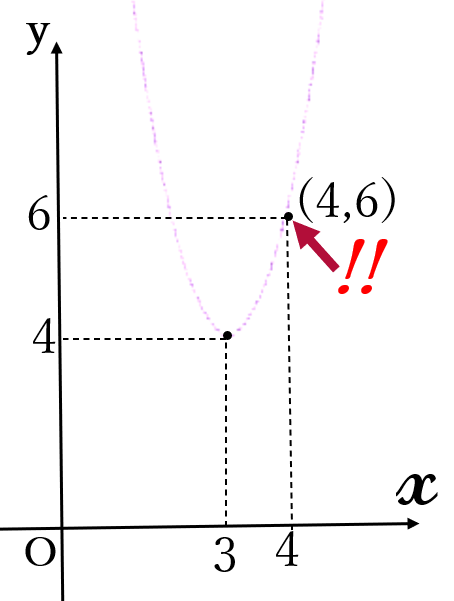
\((\ast) \ \)の放物線と\( \ y \ \)軸との交点は\( \ (0, \ 22) \ \)となって、グラフに書き込めません。その場合には、頂点以外の点を1つ示します。ここでは\( \ x=4 \ \)のとき\( \ y=6 \ \)になることから、\((4, \ 6 \ )\)を記します。
次ページに続く
(3) \(\Large y=2(x-3)^2+4\)
頂点\( \ (3, \ 4)\)
軸 \(x=3\)
下に凸
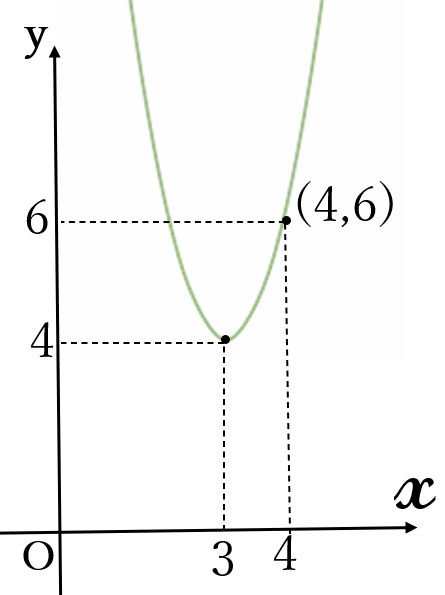
③ 頂点周辺から、下に凸の放物線を描きます。かならず、点\( \ (4, \ 6) \ \)を通るように描きます。できるだけ滑らかに描きましょう。
後に、2次関数の決定で学習しますが、放物線は頂点と頂点以外の1つの点の座標が定まれば、放物線が決定されます。頂点以外の1つの点を、必ずグラフ上に記します。
\(y=ax^2+bx+c \quad (a \neq 0)\)
のグラフ
2次関数のグラフである放物線で大切なことは、頂点の座標です。
しかし、2次関数の一般形 $$ \Large y=ax^2+bx+c (a \neq 0) $$ では、頂点の座標が解りません。
そこで、頂点の座標が解る標準形 $$ \Large y=a(x-p)^2+q (a \neq 0) $$ の形に式変形する必要があります。
この式変形が、2次関数の学習では1つのポイントになります。

この式変形を、 平方完成 といいます。
$$ \large y=ax^2+bx+c \Rightarrow y=a(x-p)^2+q $$の公式がありますが、多くの生徒にとって、公式は使いづらいようです。
はじめは、公式を使わない方法で式変形の手法を習得しましょう。公式は、後で紹介します。
「平方完成」を覚えよう!
$$ a^2+2ab+b^2=(a+b)^2 $$
という基本的な因数分解の手法を使います。
教科書と同様に、具体例で解説しますが、教科書よりも詳しく説明していきます。
平方完成
\(y=ax^2+bx+c\) において、
\(a=1\) の場合
例1 \(\large y=x^2+4x+5\)

①\(x\)の係数を
\(2\)で割った数を
\((x )^2\)の中に
入れます。
②\((x )^2\)の中に
入れた数の
2乗を引きます。
③定数項はそのまま降ろします。
例2 \( y=x^2-6x+7\)
\(x\)の係数\(-6\)を2で割った数(\(-6\)の半分)\(-3\) を、\((x )^2\)の中に入れます。$$ \Large \Downarrow $$ $$ \large y=(x-3)^2 $$
\((x )^2\)の中に入れた数 \(-3\) の2乗を引きます。定数項の \(7\) は、そのまま降ろします。$$ \large \Downarrow $$ $$ \large y=(x-3)^2-(-3)^2+7 $$
後は、整理して完成です。$$ \Large \Downarrow $$ $$ \large y=(x-3)^2-9+7=(x-3)^2-2 $$
例3 \( y=x^2+3x-1\)
\(x\)の係数\(3\)を2で割った数(\(3\)の半分)\(\large \frac{3}{2} \ \)を、\((x )^2\)の中に入れます。$$ \Downarrow $$ \( y=\left(x+ \frac{3}{2} \right)^2\)
\((x )^2\)の中に入れた数\( \ \large \frac{3}{2} \ \)の2乗を引きます。定数項の \(-1\) は、そのまま降ろします。$$ \Downarrow $$ \( y=\left(x+ \frac{3}{2} \right)^2-\left(\frac{3}{2} \right)^2-1 \)
後は、整理して完成です。$$ \Downarrow $$ \( y=\left(x+\frac{3}{2} \right)^2-\frac{9}{4}-1=\left(x-\frac{3}{2} \right)^2-\frac{13}{4} \)
\(y=ax^2+bx+c\) において、
\(a \neq 1,a \neq 0\) の場合
例4 \( y=2x^2-4x+1\)
\(2x^2-4x \ \)を\( \ x^2 \ \)の係数\( \ 2 \ \)でくくります。$$ \Downarrow $$ $$ \large y=2(x^2-2x)+1 $$
\((x^2-2x) \ \)の中の\( \ x^2-2x \ \)だけを、例1~例3と同様の手法で平方完成します。$$ \Downarrow $$ $$ \large y=2\{(x-1)^2-1\}+1 $$
\(\{ \quad \} \ \)をはずして、整理して完成です。$$ \Downarrow $$ $$ \large y=2(x-1)^2-2+1=2(x-1)^2-1 $$
例5 \( y=-2x^2-6x+2\)
\(-2x^2-6x \ \)を\( \ x^2 \ \)の係数\( \ -2 \ \)でくくります。$$ \Downarrow $$ $$ y=-2(x^2+3x)+2 $$
\((x^2+3x) \ \)の中の\( \ x^2+3x \ \)だけを、例1~例3と同様の手法で平方完成します。$$ \Downarrow $$ \(y=-2\left \{\left (x+\frac{3}{2} \right)^2-\left(\frac{3}{2}\right)^2\right\}+2\)
\(=-2\left \{\left (x+\frac{3}{2} \right)^2-\frac{9}{4}\right\}+2\)
\(\{ \quad \} \ \)をはずして、整理して完成です。$$ \Downarrow $$ \(y=-2\left (x+\frac{3}{2} \right)^2+\frac{9}{2}+2 \)
\(=-2\left (x+\frac{3}{2} \right)^2+\frac{13}{2}\)
例6 \( y=-\frac{1}{2}x^2+3x-2\)
\(-\frac{1}{2}x^2+3x \ \)を\( \ x^2 \ \)の係数\( \ -\frac{1}{2} \ \)でくくります。$$ \Downarrow $$ $$ \large y=-\frac{1}{2}(x^2-6x)-2 $$
\((x^2-6x) \ \)の中の\( \ x^2-6x \ \)だけを、例1~例3と同様の手法で平方完成します。$$ \Downarrow $$ $$ \large y=-\frac{1}{2}\{(x-3)^2-3^2\}-2 $$
\(\{ \quad \} \ \)をはずして、整理して完成です。$$ \Downarrow $$ $$ y=-\frac{1}{2}(x-3)^2+\frac{9}{2}-2=-\frac{1}{2}(x-3)^2+\frac{5}{2} $$
