暗算でサクサク図形問題４

問題１５

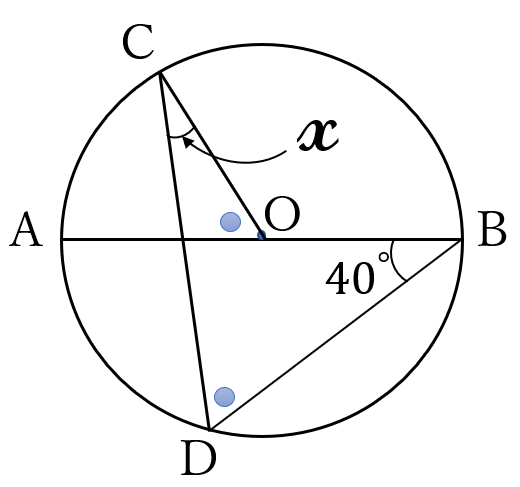
　右の図で、点\(O\)は線分\(AB\)を直径とする円の中心であり、２点\(C, \ D\)は、円\(O\)の周上にある。４点\(A, \ B, \ C, \ D\)　は、図のように、\(A, \ C, \ B, \ D\)の順に並んでおり、互いに一致しない。点\(O\)と点\(C\)、点\(A\)と点\(C\)、点\(B\)と点\(D\)、点\(C\)と点\(D\)をそれぞれ結びます。\(\angle AOC=\angle BDC, \ \angle ABD=40^{\circ}\)のとき、\(x\)で示した\(\angle OCD\)の大きさを求めなさい。

解答

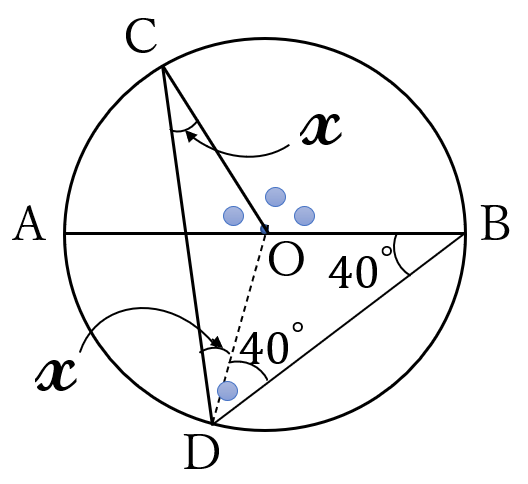
（答）　\(\Large 20^{\circ}\)

\(\triangle OBD, \ \triangle OCD \ \)は
二等辺三角形だから、
\(\angle ODB=\angle OBD\)
\(=40^{\circ}\)
\(\angle ODC=\angle OCD\)
\(=x\)　　よって
\(\angle BDC=x+40^{\circ}\)
\(\angle AOC=\angle BDC\)　だから、
\(\angle AOC=x+40^{\circ} \ \cdots \ (\ast)\)
また、円周角と中心角の関係より
\(\angle BOC=2\angle BDC=2\angle AOC\)
　よって、\(\angle AOC + \angle BOC =180^{\circ}\)　だから
\(\angle AOC + \angle BOC=\angle AOC + 2\angle AOC\)
\(=3\angle AOC=180^{\circ}\)　よって、\(\angle AOC=60^{\circ}\)
\((\ast)\)より、\(x+40^{\circ}=60^{\circ},\quad x=20^{\circ}\)

ごちゃごちゃ書いてますが、図の\( \ \circ \ \)1個が\( \ 60^{\circ} \ \)です。

問題４５

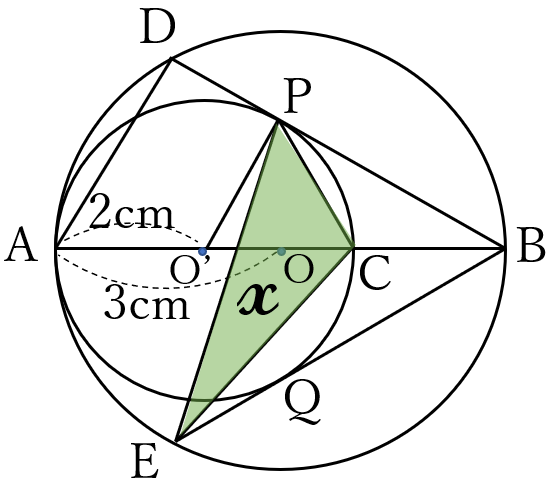
　右の図のように、
線分\(AB\)を直径とする
円\(O\)があります。
また、線分\(AB\)上に
点\(A, \ B\)と異なる点\(C\)を
とり、線分\(AC\)を直径と
する円を円\(O’\)とします。
　点\(B\)から円\(O’\)に２つの
接線をひき、接点をそれ
ぞれ\(P, \ Q\)とします。
　さらに、２つの直線\(BP, \ BQ\)と円\(O\)との交点で、
\(B\)以外の点をそれぞれ\(D, \ E\)とします。
　円\(O\)の半径を\(3 \ cm\)、円\(O’\)の半径を\(2 \ cm\)とするとき、
\(\triangle CPE\)の面積\(\large x\)を求めなさい。

　図形は複雑ですが、計算は極めてシンプルで、暗算で計算できます。

解答

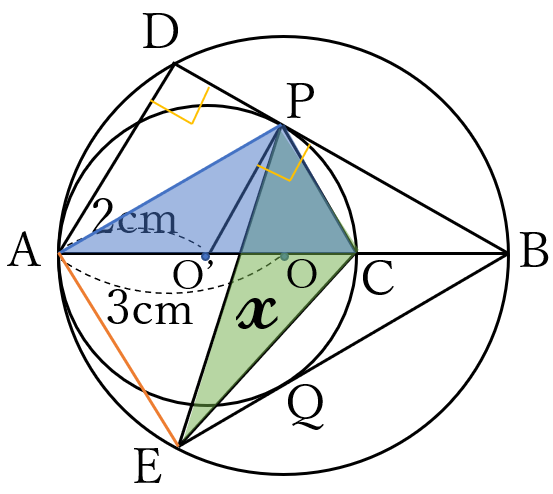
（答）\(\Large 2\sqrt{3}\)　\((cm^2)\)　

点\(A\)と点\(P\)、
点\(A\)と点\(E\)を結びます。
\(PC//AE \ \cdots \ (\ast)\)
よって、\(\triangle PEC=\triangle PAC\)
ゆえに
\(\triangle PEC=\triangle PAC\)
\(=PA\cdot PC\cdot \frac{1}{2}\)
\(=2\sqrt{3}\times 2\times \frac{1}{2}=2\sqrt{3} \ \cdots \ (\ast \ast)\)

\(PO=\sqrt{3}\)　を使えば
\(\triangle PAC = AC\cdot PO\times \frac{1}{2} =4\times \sqrt{3} \times \frac{1}{2}=2\sqrt{3}\)

\((\ast)(\ast \ast) \ \)の説明は、次ページ

直線\(BD\)は、円\(O’\)の接線。
点\(P\)はその接点だから
\(\angle O’PB =90^{\circ} \ \)　また
\(O’B=4cm\)
\(PO’=2cm\)　だから
\(\triangle PBO’\)は、\(2:1:\sqrt{3}\)
の直角三角形。よって
\(\angle PO’B =60^{\circ}\)　ゆえに
\(\triangle PO’C\)は、正三角形で
\(PC=2cm, \ \angle PCA =60^{\circ} \ \cdots\)①
また\( \ AC=4cm, \ \angle APC=90^{\circ}\)だから
\(\triangle PAC \equiv \triangle PBO’ \ \)で、\(PA=PB=2\sqrt{3} \ \cdots\)②
さらに\( \ \angle ADB = \angle O’PB = 90^{\circ} \ \)ゆえ\( \ \ DA//PO’\)
よって、\(\angle DAB = \angle PO’B =60^{\circ}\)
\(\triangle AEB\)と\(\triangle ADB\)は直線\(AB\)に関して対称なので
\(\angle EAB =\angle DAB =60^{\circ} \ \cdots\)③
①③より錯角が等しいので\( \ PC//AE\)　また、①②より
\(\triangle PAC =PA\cdot PC\cdot \frac{1}{2}=2\sqrt{3}\times 2\times \frac{1}{2}=2\sqrt{3}\)

問題２４

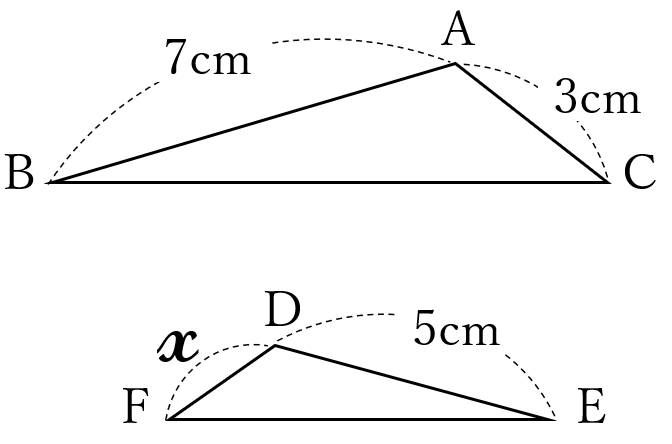
下の図で、\(\triangle ABC \ \)∽\( \ \triangle DEF \ \)であるとき、\(\large x \ \)の値を求めてください。

解答

（答）　\(\Large \frac{15}{7}\)　\((cm)\)

\(\triangle ABC\)において、\(AC\)は\(AB\)の\(\frac{3}{7}\)倍
\(\triangle ABC \ \)∽\( \ \triangle DEF\)より、
\(\triangle DEF\)において、\(DF\)も\(DE\)の\(\frac{3}{7}\)倍だから
\(\large x\)\((DF)=DE\times \frac{3}{7}=5\times \frac{3}{7}=\frac{15}{7}\)

\(5:x=7:3 \ \)からスタートしても良いですが、暗算しづらいかもしれません。

問題２５

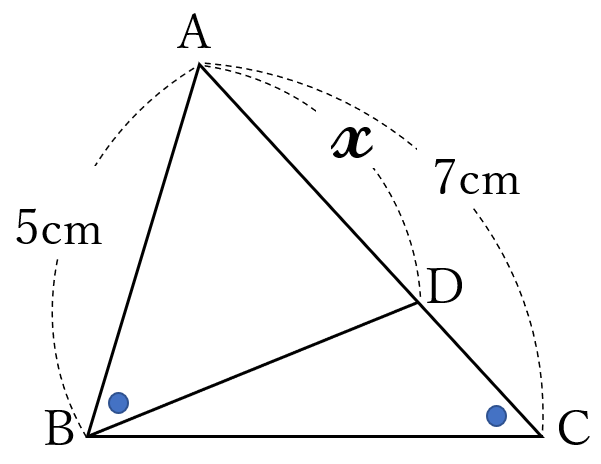
　下の図のような\(\triangle ABC \ \)があります。辺\(AC \ \)上に点\(D \ \)があり、\(\angle ACB =\angle ABD \ \)です。\(AB=5cm, \ AC=7cm \ \)のとき、\(AD \ \)の長さ\(\large x \ \)を求めなさい。

解答

（答）　\(\Large \frac{25}{7}\)　\((cm)\)

\(\triangle ABC\)と
\(\triangle ADB\)において
\(\angle ACB = \angle ABD\)
\(\angle A\)は共通
2組の角が等しいので
\(\triangle ABC \ \)∽\( \ \triangle ADB\)
よって、\(\triangle ABC\)
において、\(AB\)は\(AC\)の\(\frac{5}{7}\)倍だから
\(\triangle ADB\)において、\(AD\)は\(AB\)の\(\frac{5}{7}\)倍です。
したがって、\(\large x\)\((AD)=AB\times \frac{5}{7}=5\times \frac{5}{7}\)\(\large =\frac{25}{7}\)

問題３３

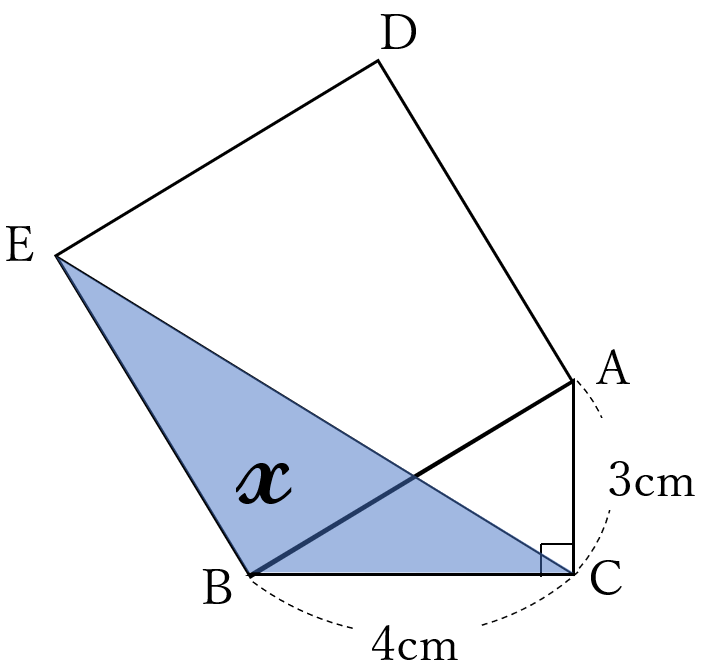
　下の図のように\(\angle ACB=90^{\circ} \ \)の直角三角形\(ABC \ \)と、辺\(AB \ \)を1辺とする正方形\(ABED \ \)があります。線分\(EC \ \)をひきます。
　\(BC=4cm, \ AC=3cm \ \)のとき、
\(\triangle EBC \ \)の面積\( \ \large x \ \)を求めなさい。

解答

（答）　\(\Large 8\)　\((cm^2)\)

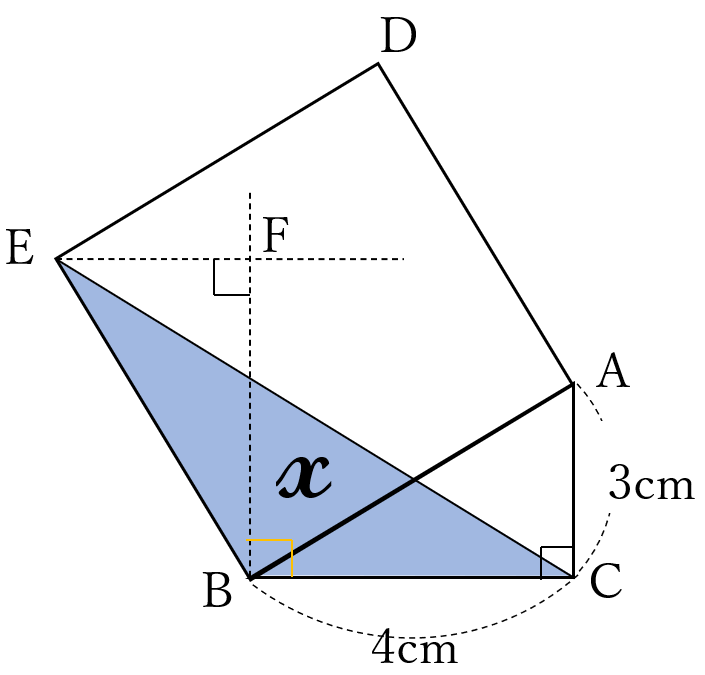
右の図のように、
点\(E\)を通り辺\(BC\)に
平行な直線と
点\(B\)を通り辺\(AC\)に
平行な直線との交点を
\(F\)とします。
\(\triangle ABC\equiv \triangle EBF\)
\(\cdots \ (\ast)\)（証明下）ゆえ
\(BF=BC=4cm \ \)　よって、
\(\large x\)\((\triangle EBC)=BC\cdot BF\times \)\(\large \frac{1}{2}\)\(=4\times 4\times \)\(\large \frac{1}{2}=8\)

\((\ast)\)\(\triangle ABC\)と\(\triangle EBF\)において、\(AB=EB \ \)また、
\(\angle ABC=\angle EBC-90^{\circ},\angle EBF=\angle EBC-90^{\circ}\)
だから\(\angle ABC =\angle EBF \ \)よって、直角三角形において、斜辺と一つの鋭角が等しいので、\(\triangle ABC\equiv \triangle EBF\)

　有名な問題です。問１の応用です。

問題７

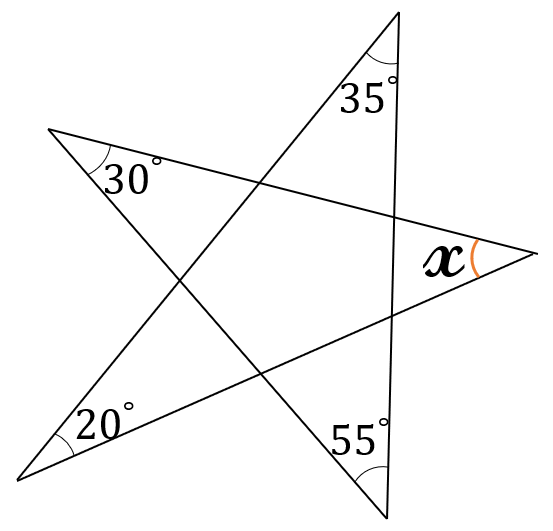
　下の図の\( \ \angle x \ \)の大きさを求めてください。

解答

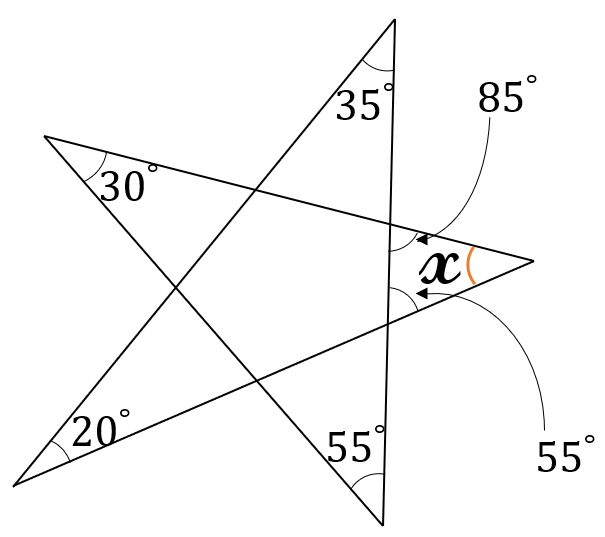
（答）　\(\Large x = 40^{\circ}\)

右図の通り
\(x=180^{\circ}-85^{\circ}-55^{\circ}\)
　\(=40^{\circ}\)

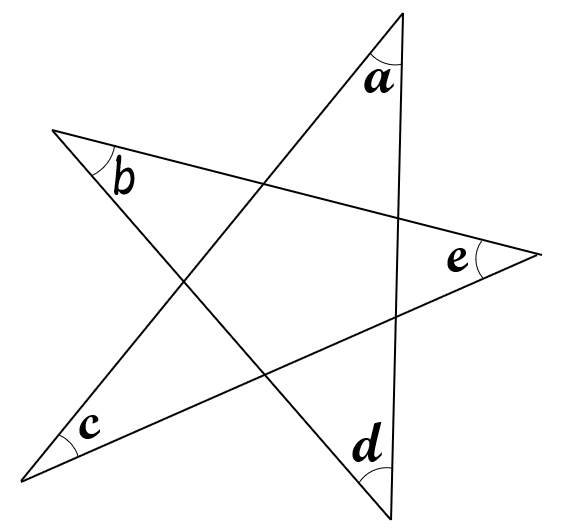
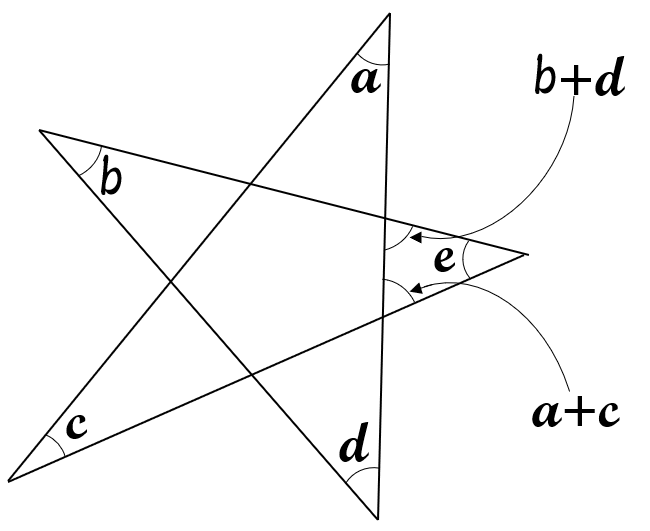
星形の5つの尖がった（とがった）角をたすと\(180^{\circ}\)になります。

下の図において、\( a + b + c + d + e = 180^{\circ}\)　です。

問題８

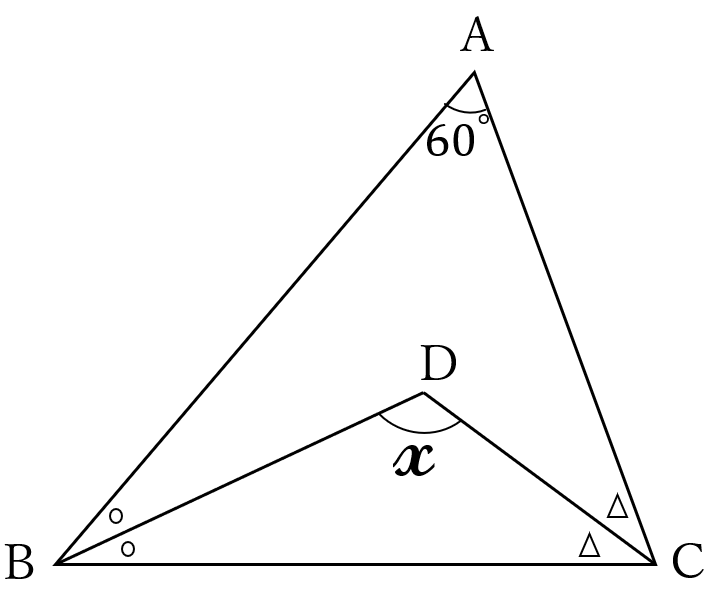
\(\triangle ABC\)と\(\triangle DBC\)において、

\(\angle BAC = 60^{\circ}\)
\(\angle ABD =\angle CBD, \ \angle ACD = \angle BCD\)

です。

\( \ \angle BDC \ \)の大きさ\( \ x \ \)を求めてください。

解答

（答）　\(\Large x=120^{\circ}\)

右図において、\( \ \circ \ + \ \)\(\tiny{\triangle}\)\( \ =K \ \)とおきます。

\(\triangle ABC \ \)において、\(2K+60^{\circ}=180^{\circ}\)

よって、\(K=60^{\circ}\)

\(\triangle DBC \ \)において、\(x+K=180^{\circ}\)

ゆえに、\(x=180^{\circ}-K=180^{\circ}-60^{\circ}=120^{\circ}\)

問５を使えば、
\(x=60^{\circ} + K=60^{\circ}+60^{\circ}=120^{\circ}\)　　です。

問題９

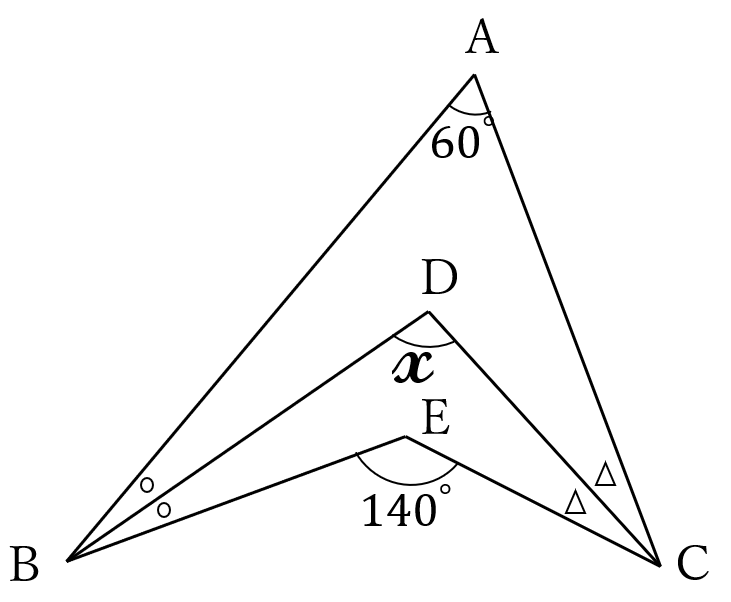
右の図において

\(\angle BAC = 60^{\circ}\)
\(\angle BEC = 140^{\circ}\)
\(\angle ABD = \angle EBD\)
\(\angle ACD = \angle ECD\)

です。

\(\angle BDC \ \)の大きさ\( \ x \ \)を求めてください。

解答

（答）　\(\Large x=100^{\circ}\)

右図において、\( \ \circ \ + \ \)\(\tiny{\triangle}\)\( \ =K \ \)とおきます。

図形\(ABEC\)において、\(2K+60^{\circ}=140^{\circ}\)　⇐問題５

よって、\(K=40^{\circ}\)

ゆえに、図形\(ABDC\)において、

\(x=60^{\circ}+K=60^{\circ}+40^{\circ}=100^{\circ}\)　⇐問題５

問題２、問題３の応用です。

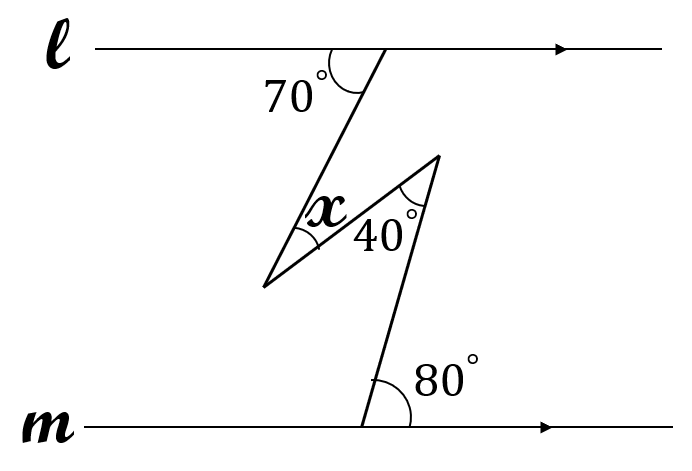
問題４

下の図で、\(l \ // \ m \ \)です。

\(\angle x \ \)の大きさを求めてください。

解答

（答）　\(\Large x=30^{\circ}\)

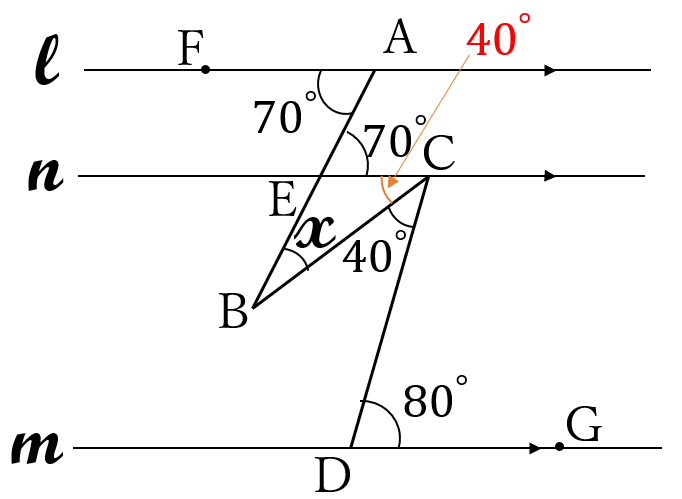
下の図において、\(l \ // \ n \ // \ m \ \)です。

\(\angle FAE =\angle AEC =70^{\circ} \ \cdots \ (\ast)\)　（錯角）
\(\angle ECD = \angle CDG =80^{\circ} \ \)（錯角）　だから、\(\angle ECB = \angle ECD – 40^{\circ}=80^{\circ}-40^{\circ}=40^{\circ}\)
よって、\((\ast) \ \)より、\(x+40^{\circ}=70^{\circ}\)
\(x=30^{\circ}\)

問題４９

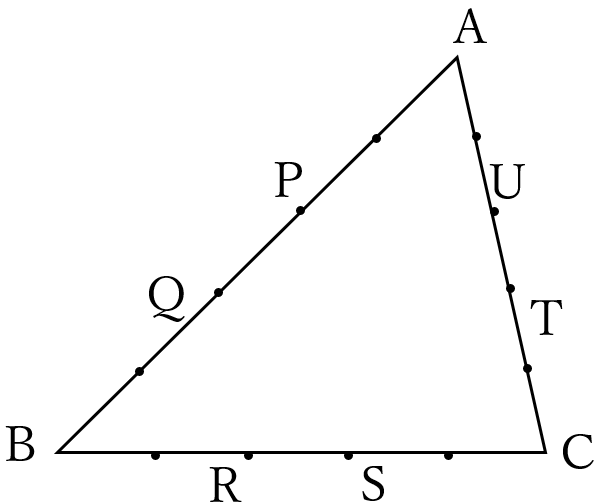
右図のように、\(\triangle ABC \ \)の各辺上に、各辺を5等分する点をとります。それらの点のなかで、各辺を\(2:3, \ 3:2 \ \)に分ける点をそれぞれ\(P,Q,R,S,T,U\)とします。

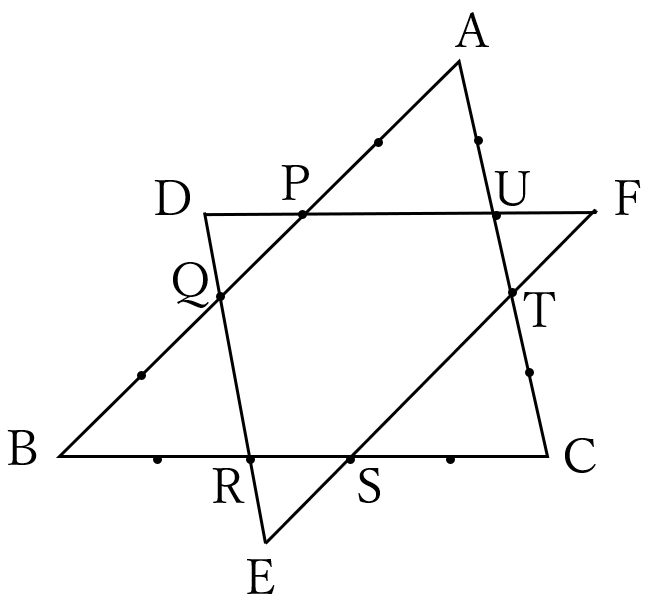
３直線、\(PU,QR,ST \ \)で囲まれてできる三角形を\( \ \triangle EFD \ \)とすると、\(\triangle ABC \ \)∽\( \ \triangle EFD \ \)です。
\(\triangle ABC \ \)と\( \ \triangle EFD \ \)の相似比を求めてください。

解答

（答）　\(\Large \triangle ABC \ : \ \triangle EFD =5:4\)

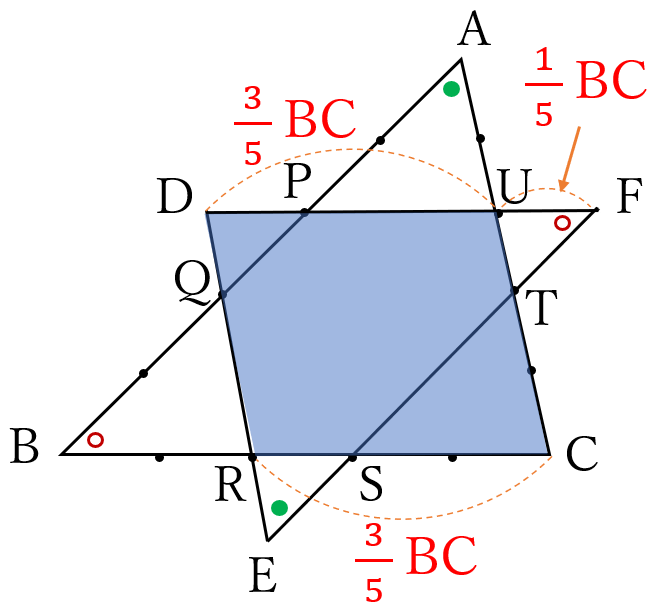
平行線と線分の比
（巻末資料参照）より、

\(PU//BC, \ QR//CA\)
\(TU//DE\)

よって、四角形\(DRCU\)
は、平行四辺形です。

したがって、
\(DU=RC=\frac{3}{5}BC \ \cdots\)①
また、\(UF//CS \ \)ゆえ\( \ \triangle TSC \ \)∽\( \ \triangle TFU\)
\(CT:UT=2:1 \ \)だから、\(SC:FU=2:1\)
よって、\(FU=\frac{1}{2}SC=\frac{1}{5}BC \ \cdots\)②
①②より、\(FD=\frac{4}{5}BC\)
ゆえに、求める\( \ \triangle ABC \ \)と\( \ \triangle EFD \ \)の相似比は、
\(BC:FD=5:4\)

問題１６

　下の図で、\(\angle x \ \)の大きさを求めてください。
　ただし、点\( \ O \ \)は、円の中心で、線分\( \ AC \ \)は、この円の直径です。

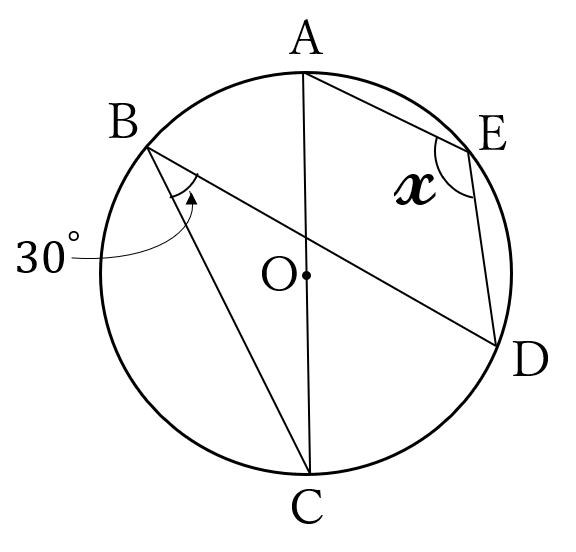
解答

（答）　\(\Large x=120^{\circ}\)

下の図の通りです。

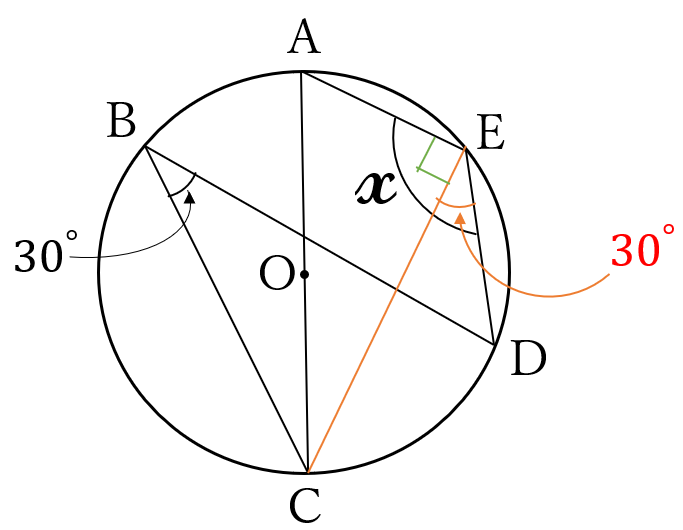
\(\Large x=90^{\circ}+30^{\circ}=120^{\circ}\)

問題１７

下の図で、\(\angle x \ \)の大きさを求めてください。

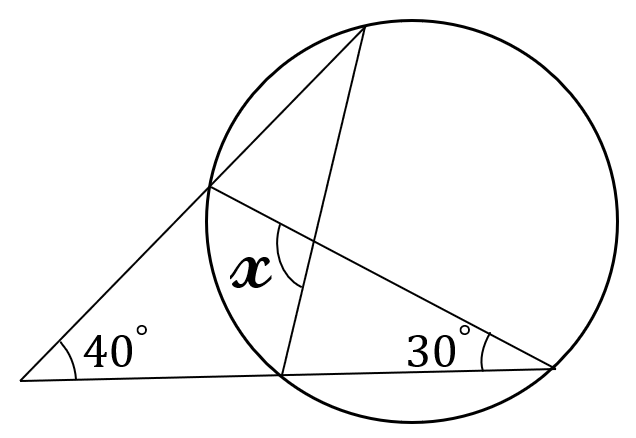
解答

（答）　\(\Large x=100^{\circ}\)

下の図の通りです。

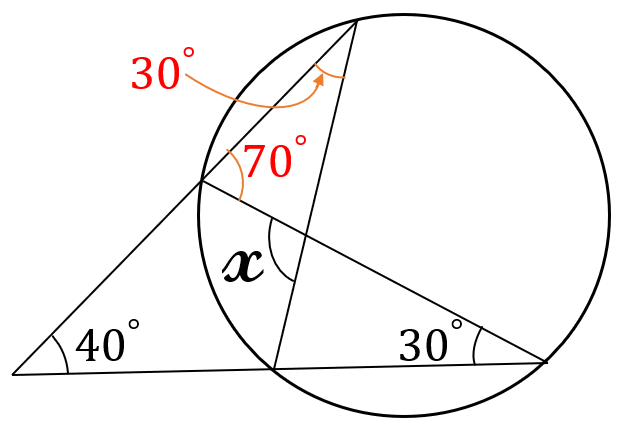
\(\Large x=70^{\circ}+30^{\circ}=100^{\circ}\)

問題２０

下の図で、\(\angle x \ \)の大きさを求めてください。
　ただし、点\( \ O \ \)は円の中心です。

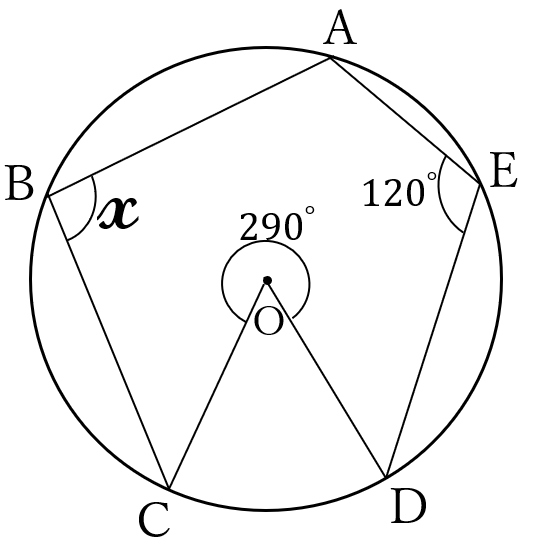
解答

（答）　\(\Large x=95^{\circ}\)

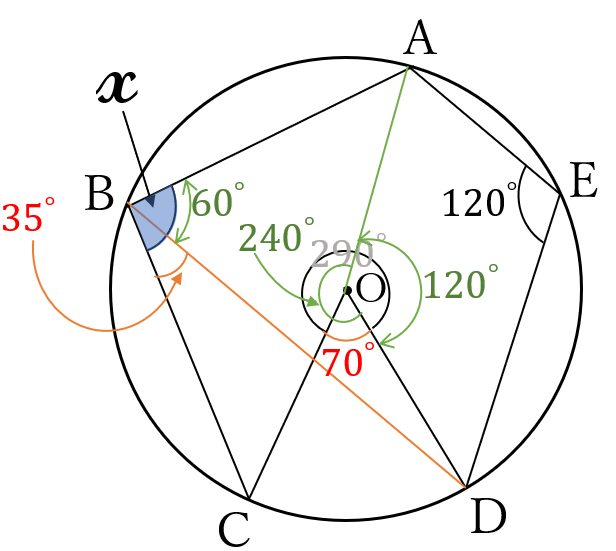
点\(B\)と点\(D\)を
結びます。

小さい方の\(\angle COD=360^{\circ}-290^{\circ}=70^{\circ}\)
中心角と円周角の関係から\(\angle CBD=\frac{1}{2} \angle COD=35^{\circ}\)
中心角と円周角の関係から
大きい方の\(\angle AOD=\angle AED \times 2=240^{\circ}\)
よって、小さい方の\(\angle AOD =360^{\circ}-240^{\circ}=120^{\circ}\)
中心角と円周角の関係から\(\angle ABD=\frac{1}{2} \angle AOD=60^{\circ}\)
ゆえに、\(x=\angle CBD + \angle ABD = 35^{\circ}+60^{\circ}=95^{\circ}\)