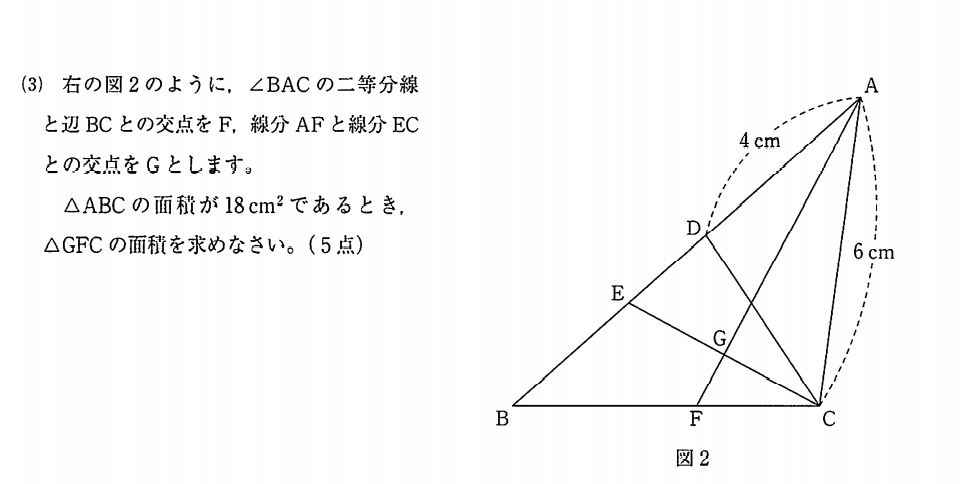
大問4(3)の面積問題。(1)(2)は、学校選択問題と異なるが、(3)は、学校選択問題と共通である。少し解きづらい問題かもしれない。角の二等分線と辺の比がメインになっている。
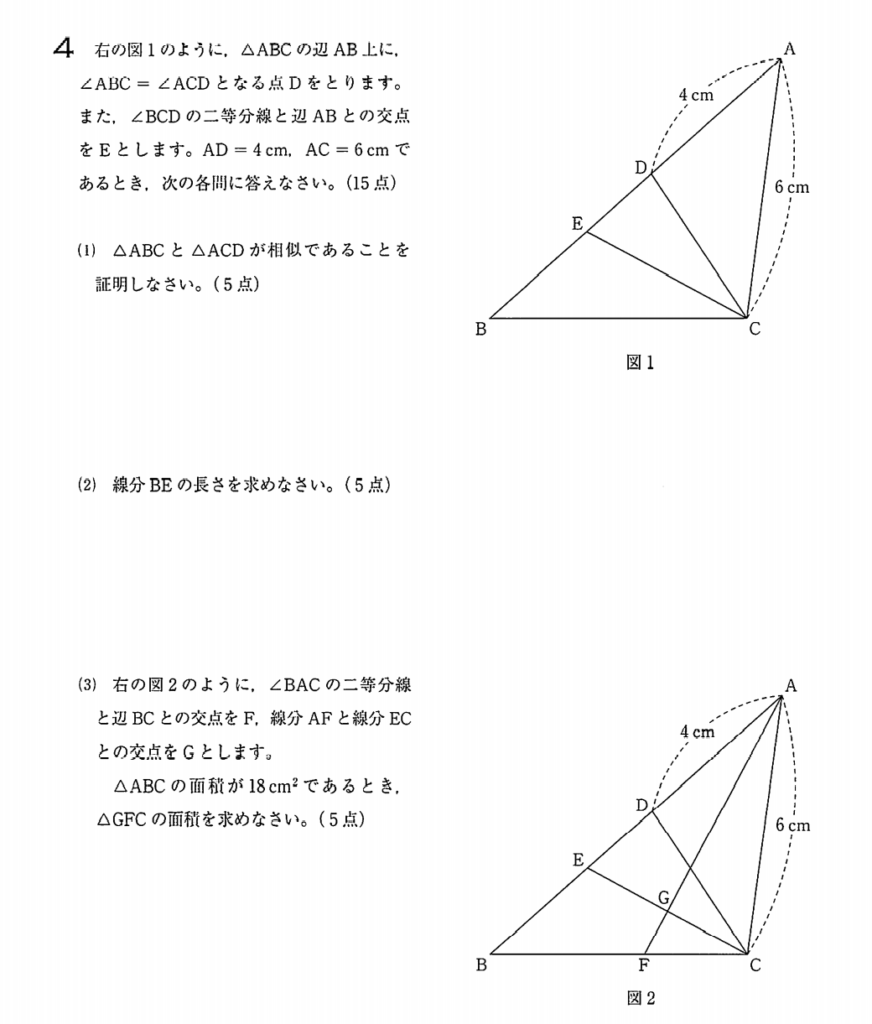
(1)(2)で解っていること
\(\triangle ABC \sim \triangle ACD\)
\(AB=9\) \(BE=3\) \(ED=2\)
(3)の解答例
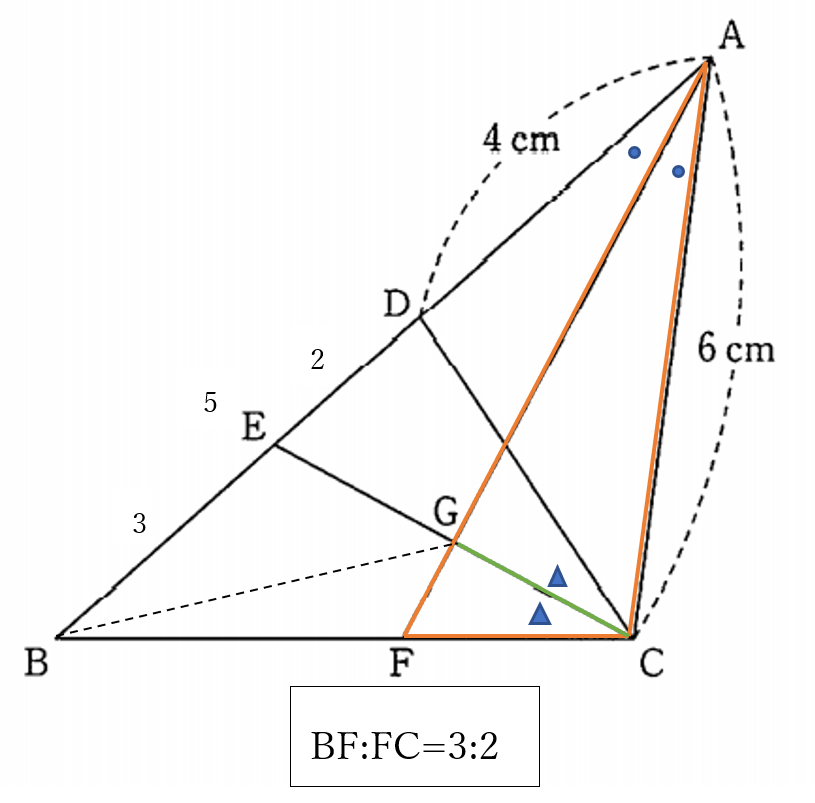
\(AE=6\)だから\(\triangle ABC\)は
\(AE=AC\)の二等辺三角形
\(AF\)は\(\angle BAC\)の二等分線だから
\(EG=GC\)
また、\(BF:FC=3:2\)
線分の長さの比で、次の順で計算する。
\(\triangle ABC \rightarrow \triangle EBC\)
\(\rightarrow \triangle GBC \rightarrow GFC\)
\(\triangle ABC \times \frac{1}{3} \times \frac{1}{2} \times \frac{2}{5}\)
\(=\triangle ABC \times \frac{1}{15}=18\times \frac{1}{15}\)
\(=\frac{6}{5}=\triangle GFC\)
(答)\(\displaystyle \frac{6}{5}\) \((cm^2)\)
【別解】
\(AB:AC=BF:FC=3:2\)
\(\iff \triangle AFC=\frac{2}{5}\triangle ABC\)
\(=\frac{2}{5} \times 18=\frac{36}{5}\cdots\) ①
\(BE:AE=1:2\) だから
\(\triangle AEC=\frac{2}{3}\triangle ABC=\frac{2}{3} \times 18=12\)
\(AC=AE\) だから \(EG=GC\)
\(\iff \triangle AGC=\frac{1}{2} \triangle AEC\)
\(=\frac{1}{2} \times 12=6\)
よって ①より
\(\triangle GFC=\triangle AFC-\triangle AGC\)
\(=\frac{36}{5}-6=\frac{6}{5}\)
(答)\(\displaystyle \frac{6}{5}\) \((cm^2)\)