次は、宮城県のお隣、山形県。ここでも思考を要する問題だけを取り扱う。
大問3⃣
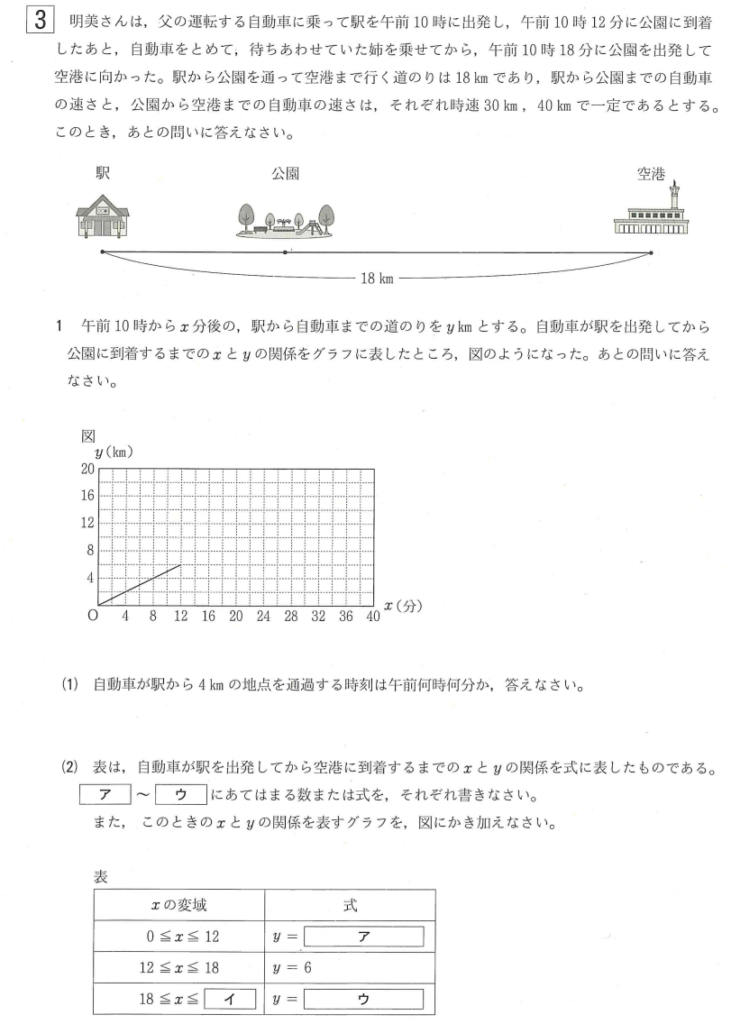

問題文の自動車の速度は時速であるが、グラフは分速である。分速で考え、時速に直して答えることが必要。1の(2)から解答していこう。
3⃣1(2)解答例
時速\(30km\)より、分速は
\(\frac{30}{60}=\frac{1}{2}km/分\)
または、グラフより、\(y=\frac{6}{12}x\)
よって、
ア \(y=\frac{1}{2}x\)
アの(答) \(\large y=\frac{1}{2}x\)
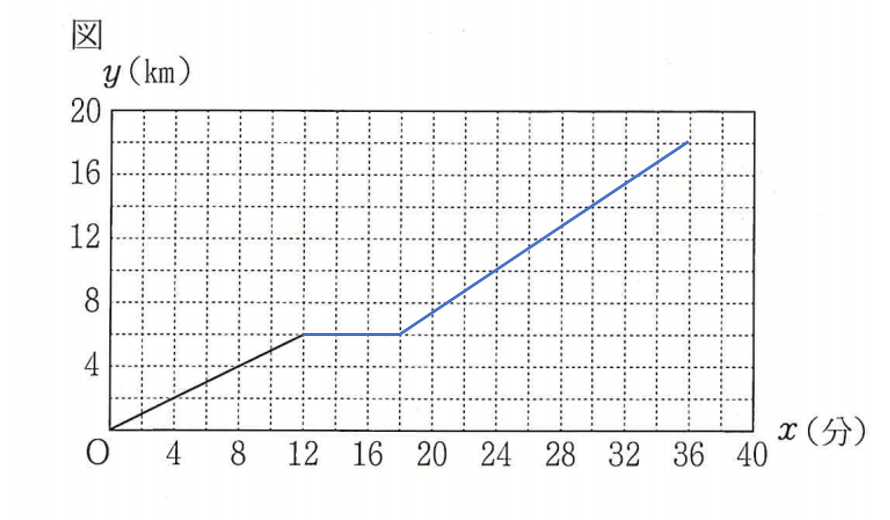
家を出て18分後に、公園を出発して時速\(40km\)で空港に向かった。分速は\(\frac{40}{60}=\frac{2}{3} \ km/分\) である。
したがって、グラフは、12分から18分までは\(6km\)のままで距離は変わらず(横線)。18分からは傾き\(\frac{2}{3}\)の直線を、距離\(18km\)まで描けばよい。
グラフ(答) 右図
公園から空港までは\(18-6=12km\)だから、公園から空港までに要した時間は
\(\displaystyle \frac{12}{\frac{2}{3}}=18分\)
したがって、家を出てから空港に着くまでの経過時間は
\(18+18=36分\)
求める式は、
\(y-6=\frac{2}{3}(x-18) \iff y=\frac{2}{3}x-6\)
イの(答) \(36\) 、ウの(答) \(\displaystyle y=\frac{2}{3}x-6\)
3⃣1(3)解答例
駅から公園までは\(6km\)
10時6分に駅を出たバスは、10時12分より前に公園に着いてないから、その時の分速は
\(\frac{6}{12-6}=1km/分\) より遅い
よって、時速\(60km\) より遅い
そして、10時18分より前には公園に着いているはずだからその時の分速は
\(\frac{6}{18-6}=\frac{1}{2}km/分\) より速い
よって、時速\(30km\) より速い
また、10時36分より後に、空港に着いているはずだから、その時の分速は
\(\frac{18}{36-6}=\frac{3}{5}km/分\) より遅い
よって、時速\(36km\) より遅い
以上より
ェの(答) \(30\)
オの(答) \(36\)
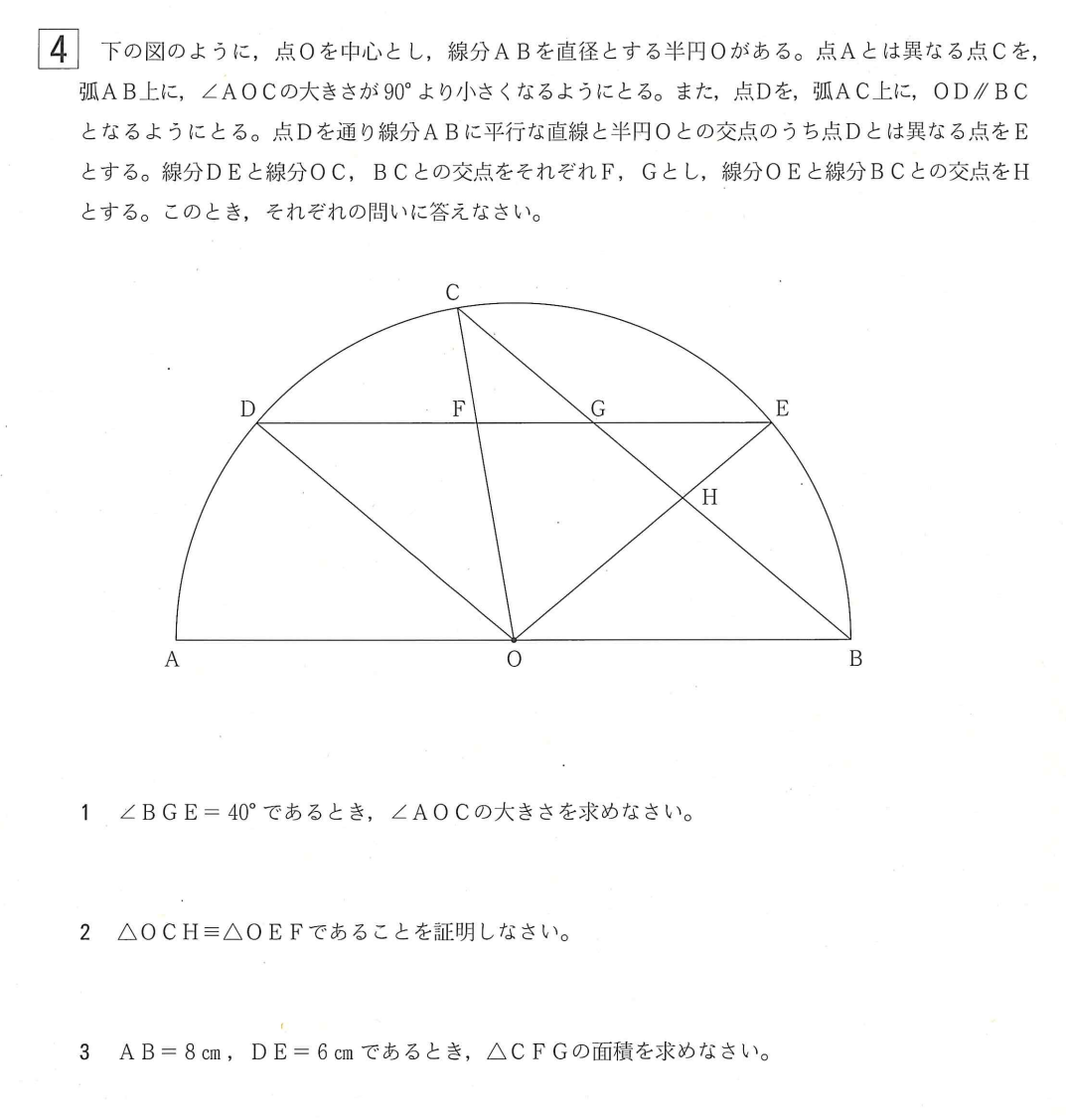
大問4⃣3の面積問題
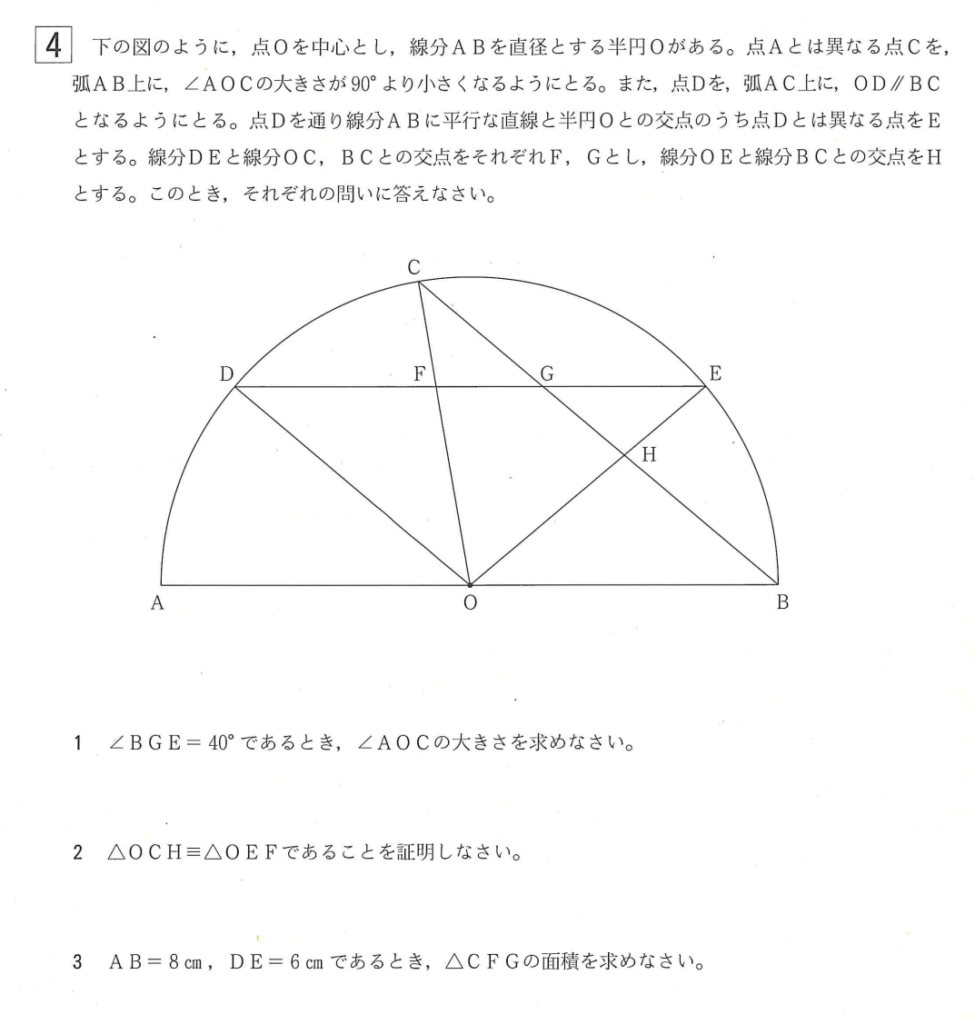
解答例
\(\triangle ODE \equiv \triangle OCB\) だから
\(CB=6\)
\(O\)から線分\(CB\)に下した垂線の足を\(I\) とおくと
\(BI=3\) よって
\(OI=\sqrt{4^2-3^2}=\sqrt{7}\)
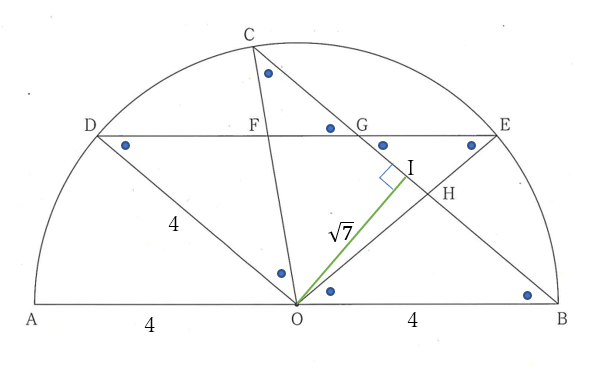
\(\triangle COB\)の面積は
\(\triangle COB=6\times \sqrt{7}\times\frac{1}{2}\)
\(=3\sqrt{7}\)
\(\triangle COB \sim \triangle CFG\) で
\(CB=6, \quad GB=4\) だから
\(CB:CG=6:2=3:1\)
よって、\(\triangle CFG\) の面積は
\(\triangle CFG=\triangle COB\times (\frac{1}{3})^2\)
\(=3\sqrt{7}\times \frac{1}{9}=\large \frac{\sqrt{7}}{3}\)
(答) \(\Large \frac{\sqrt{7}}{3}\) \((cm^2)\)