残念ながら令和3年の問題は公開されていないので(令和3年5月12日現在)、令和2年の問題から抜粋して解答する。面積問題が多数出題されているので、それらを解答してみよう。
大問5
2の解答例
1より、①は \(y=\frac{1}{2}x^2\)
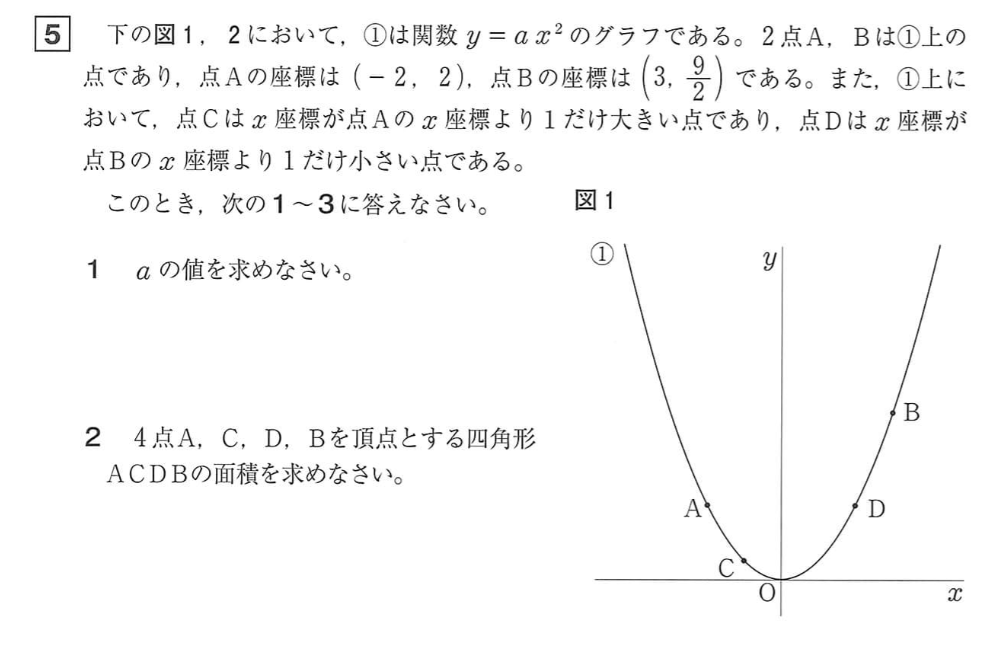
\(A(-2,2),\quad B(3,\frac{9}{2})\)
\(C(-1,\frac{1}{2}),\quad D(2,2)\)
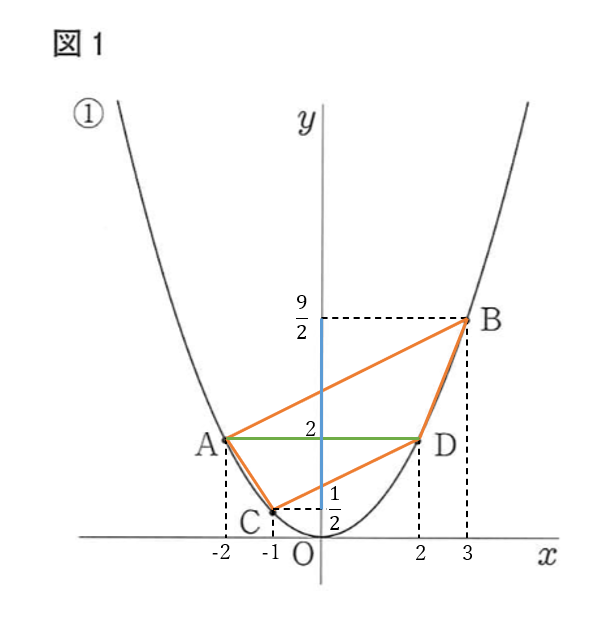
四角形\(ACDB\)の面積は、
\(\triangle ADB+\triangle ACD\)
線分\(AD\)を底辺とすれば
四角形\(ACDB\)
\(=\triangle ADB+\triangle ACD\)
\(=AD \times (\frac{9}{2}-2) \times \frac{1}{2}\)
\(+AD \times (2-\frac{1}{2})\times \frac{1}{2}\)
\(=AD \times (\frac{9}{2}-\frac{1}{2}) \times \frac{1}{2}\)
\(=4 \times 4 \times \frac{1}{2}=8\)
2の(答) \(8\)
3(2)解答例
\(E(-3,\frac{9}{2}),\quad C(-1,\frac{1}{2})\)
\(D(2,2),\quad F(4,8)\)
\(F,D,C\)から\(y\)軸に下した垂線の足をそれぞれ、\(H,I,J\)とする。
また、\(x\)軸と平行で\(E\)を通る直線と線分\(FC\)との交点を\(G\)おく。
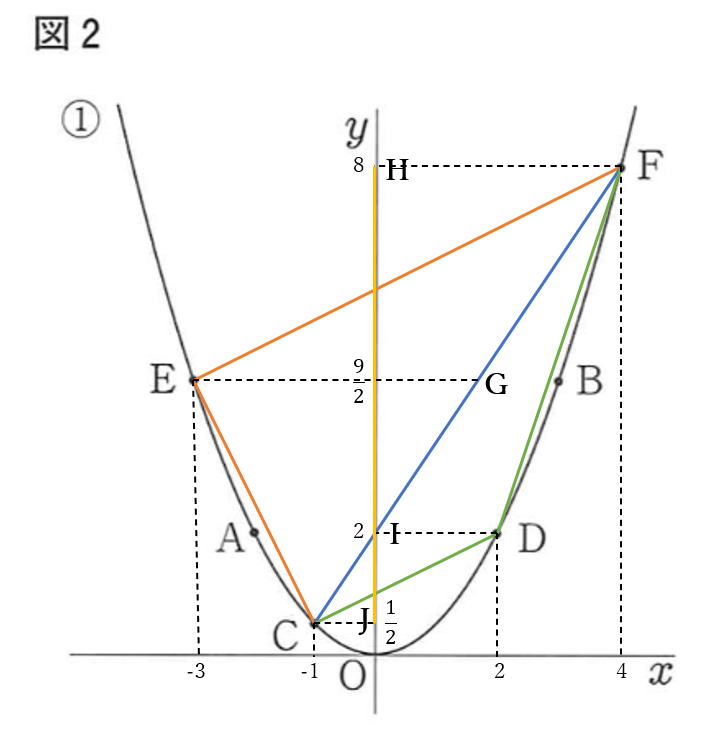
線分\(FC\)の方程式は
\(y=\frac{3}{2}x+2\)
線分\(FC\)と\(y\)軸との交点は
\(I(0,2)\)である
また、点\(G\)の\(y\)座標は
\(\frac{9}{2}\)だから
\(G\)の\(x\)座標は\(\frac{5}{3}\)
よって \(G(\frac{5}{3},\frac{9}{2})\)
したがって
\(ID=2\)
\(EG=\frac{5}{3}-(-3)=\frac{14}{3}\)
ここで
\(\triangle FEC=EG \times HJ \times \frac{1}{2}\)
\(\triangle FCD=ID \times HJ \times \frac{1}{2}\)
よって
\(\triangle FEC : \triangle FCD=EG:ID\)
\(=\frac{14}{3}:2=7:3\)
3(2)(答) 7:3
大問6
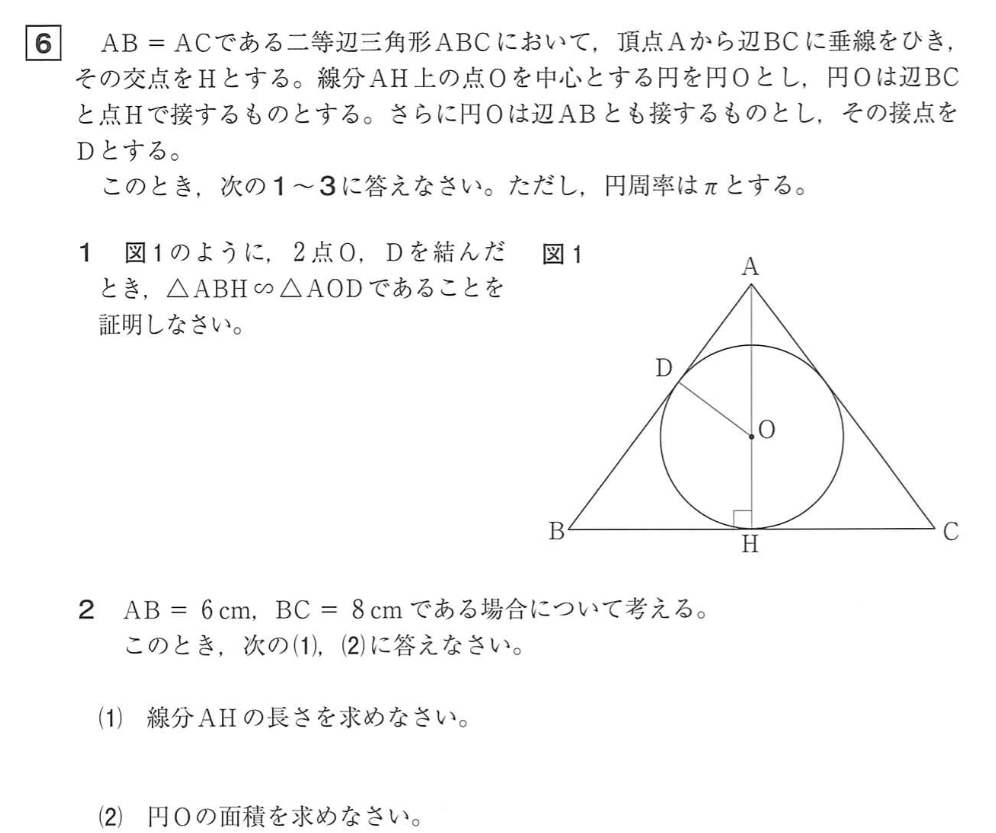
2の解答例
(1)
\(AH=\sqrt{AB^2-BH^2}\)
\(=\sqrt{6^2-4^2}=2\sqrt{5}\)
(答) \(2\sqrt{5}\) \((cm)\)
(2)
\(\angle ODA=90^{\circ},\angle OAD=\angle BAH\)
ゆえ
\(\triangle OAD \sim \triangle BAH\)
また(1)より
\(AH=2\sqrt{5}\)
さらに
\(BH=4\)
\(\iff BD=4\iff AD=2\)
よって
\(AD:OD=AH:BH\)
\(\iff 2:OD=2\sqrt{5}:4\)
\(\iff OD=\frac{4}{\sqrt{5}}\)
以上より
求める円\(O\)の面積は
\(OD^2 \times \pi=(\frac{4}{\sqrt{5}})^2 \pi\)
\(=\frac{16}{5} \pi\)
(答) \( \large \frac{16}{5} \pi\) \((cm^2)\)
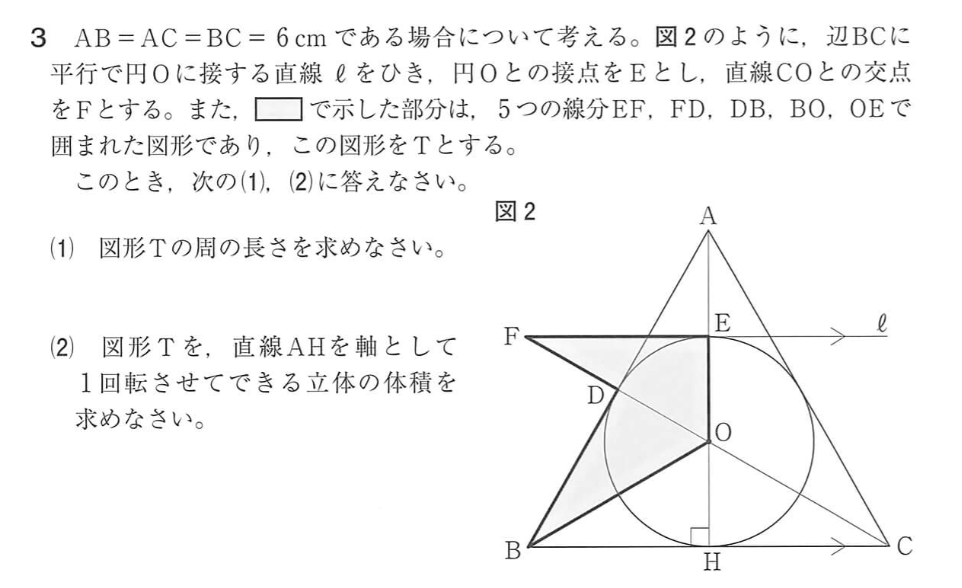
3の解答例
(1)
まず、\(\triangle ADO \equiv \triangle FEO \equiv \triangle BDO\)
\(\triangle ADO\)は
\(\angle OAD=30^{\circ},\angle DOA=60^{\circ}\)
の直角三角形だから
\(AO:OD:AD=2:1:\sqrt{3}\)
よって\(AD=3\)より
\(AO=2\sqrt{3},OD=\sqrt{3}\)
\(\iff FE=BD=3\)
\(FO=BO=2\sqrt{3}\)
\(OE=\sqrt{3}\)
\(FD=FO-OD\)
\(=2\sqrt{3}-\sqrt{3}=\sqrt{3}\)
求める図形\(T\)の周の長さは
\(FE+FD+BD+BO+OE\)
\(=6+4\sqrt{3}\)
(答) \(6+4\sqrt{3}\) \((cm)\)
(2)
右下の図のように、辺\(AC\)と円\(O\)との接点を\(I\)、\(BO\)の延長線と直線\(l\)との交点を\(G\)とおく
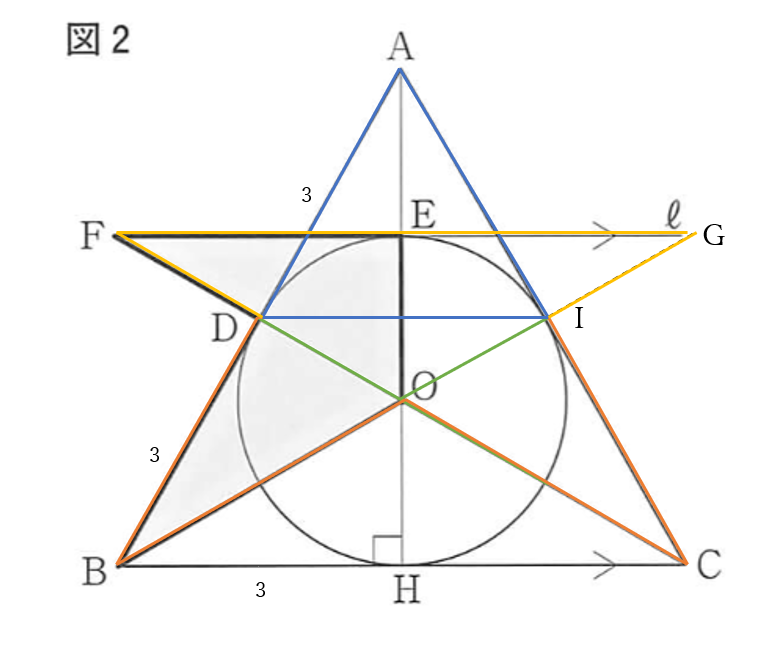
求める回転体の体積を
回転体\(DBOCI+\)回転体\(FDIG\)
で計算する。
円錐\(ABC\)の体積は
\(BH^2\pi \times AH \times \frac{1}{3}\)
\(=3^2 \pi \times 3\sqrt{3} \times \frac{1}{3}=9\sqrt{3}\pi \ \cdots\)①
円錐\(ADI\)の体積は
円錐\(ABC\)との相似比\(2:1\)より
円錐\(ABC\)の体積\( \times (\frac{1}{2})^3=\frac{9}{8}\sqrt{3}\pi \ \cdots\)②
円錐\(OFG\)と円錐\(OBC\)の体積は
円錐\(ABC\)の\(\frac{1}{3}\)だから
円錐\(ABC\)の体積\(\times \frac{1}{3}=3\sqrt{3}\pi \ \cdots\)③
円錐\(ODI\)の体積は
円錐\(OFG\)との相似比\(2:1\)より
円錐\(OFG\)の体積\(\times (\frac{1}{2})^3=\frac{3}{8}\sqrt{3}\pi \ \cdots\)➃
回転体\(FDIG\)の体積は
③④より
円錐\(OFG\)\(-\)円錐\(ODI\)
\(=3\sqrt{3}\pi-\frac{3}{8}\sqrt{3}\pi\)
\(=\frac{21}{8}\sqrt{3}\pi \ \cdots\)⑤
回転体\(DBOCI\)の体積は
①②③より
円錐\(ABC\)\(-\)円錐\(ADI\)\(-\)円錐\(OBC\)
\(=9\sqrt{3}\pi-\frac{9}{8}\sqrt{3}\pi-3\sqrt{3}\pi\)
\(=\frac{39}{8}\sqrt{3}\pi \ \cdots\)⑥
ゆえに求める立体の体積は
⑤⑥より
回転体\(DBOCI+\)回転体\(FDIG\)
\(=\frac{39}{8}\sqrt{3}\pi+\frac{21}{8}\sqrt{3}\pi\)
\(=\frac{60}{8}\sqrt{3}\pi=\frac{15}{2}\sqrt{3}\pi\)
(答) \(\large \frac{15}{2}\)\(\sqrt{3}\pi\) \((cm^3)\)
