この単元では、2次方程式の解と2次不等式の解を、2次関数のグラフ(放物線)と関係づけて求めます。
2次方程式・・・\(x \ \)の2次式で表される方程式を
\( \ x \ \)についての2次方程式といいます。
2次不等式・・・\(x \ \)の2次式で表される不等式を
\( \ x \ \)についての2次不等式といいます。
2次方程式と2次関数のグラフ
中学で学習した2次方程式は $$ \large ax^2+bx+c=0 $$ の形をしていました。
そして、解を求めるときには、因数分解できるときには $$ \large a(x-\alpha)(x-\beta)=0 $$ などと因数分解して解\( \ \alpha, \ \beta \ \)を求めました。
因数分解できないときには、解の公式 $$ \large x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} $$ を使って解を求めました。
\(\alpha, \ \beta \ \)はギリシャ文字で、
それぞれ「アルファ」「ベータ」と読みます。
ここで、2次方程式と2次関数の式(一般形)を比べてみましょう。
$$ \large \begin{eqnarray} 2次方程式 \ && ax^2+bx+c=0 \\ 2次関数 \ && y=ax^2+bx+c \end{eqnarray} $$
2次関数の式で\( \ y=0 \ \)とすると、2次方程式になることが解ります。これを視覚的に捉えようとするのがテーマです。
「2次関数\( \ y=ax^2+bx+c \ \)において、\(y=0\)」
とは、グラフ上では(図形的に)どういう意味でしょうか
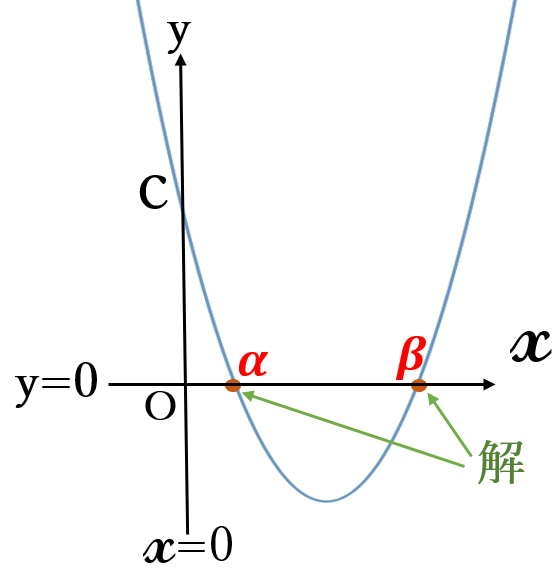
右の図のように、\(y=ax^2+bx+c \ \)のグラフが、下に凸で\( \ x \ \)軸と2点で交わっているとします。
\(x \ \)軸上では、\(y \ \)の値は\( \ 0 \ \)です。ですから、\(x \ \)軸の方程式は\( \ y=0 \ \)です。
したがって、2次関数\( \ y=ax^2+bx+c \ \)のグラフと、\(x \ \)軸との交点では\( \ y \ \)の値が\( \ 0 \ \)であり、2次関数の式は\( \ 0=ax^2+bx+c \ \)になります。これは、2次方程式の式と同じです。つまり、2次関数\( \ y=ax^2+bx+c \ \)と\( \ x \ \)軸との交点の\( \ x \ \)座標が、2次方程式\( \ ax^2+bx+c=0 \ \)の解になります。
2次方程式\( \ ax^2+bx+c=0 \ \)を解くことと、2次関数\( \ y=ax^2+bx+c \ \)のグラフと\( \ x \ \)軸との交点の\( \ x \ \)座標を求めることは同じなのです。
2次方程式を解く
$$ \Large \Updownarrow $$
2次関数のグラフ(放物線)と\( \ x \ \)軸との交点の\( \ x \ \)座標を求める。
このことから、次のことも成り立ちます。
2次方程式の実数解の個数と2次関数のグラフと\( \ x \ \)軸との共有点(交点や接点)の個数は一致します。
2次方程式の解を実数解と言います。
交点や接点を共有点と呼びます。
$$ 共有点 \begin{eqnarray} \begin{cases} & 交点 \\ & 接点 \end{cases} \end{eqnarray} $$
2次方程式$$ ax^2+bx+c=0 $$の実数解の個数を求める
$$ \Large \Updownarrow $$
2次関数$$ y=ax^2+bx+c $$のグラフと\( \ x \ \)軸との共有点の個数(位置関係)を求める
例題6
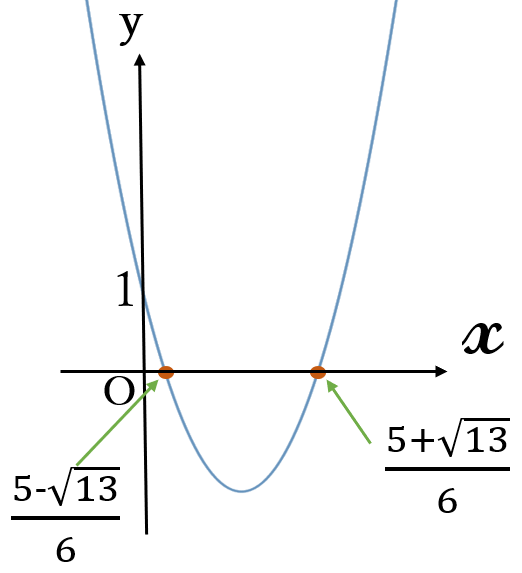
2次関数\( \ y=3x^2-5x+1\)
のグラフと\( \ x \ \)軸の共有点の座標を求めなさい。
解答
2次方程式\( \ 3x^2-5x+1=0\)
を解くと
$$ \begin{eqnarray} x &=& \frac{-b \pm \sqrt{b^2-4ac}}{2a} \\ &=& \frac{-(-5) \pm \sqrt{(-5)^2-4\times 3 \times 1}}{2\times 3} \\ &=& \frac{5\pm \sqrt{13}}{6} \end{eqnarray}$$
(答) \(\large \left(\frac{5- \sqrt{13}}{6}, \ 0 \right), \quad \left(\frac{5+ \sqrt{13}}{6}, \ 0 \right)\)
練習11
2次関数 $$ \large y=4x^2+12x+9 $$のグラフと\( \ x \ \)軸の共有点の座標を求めなさい。
解答
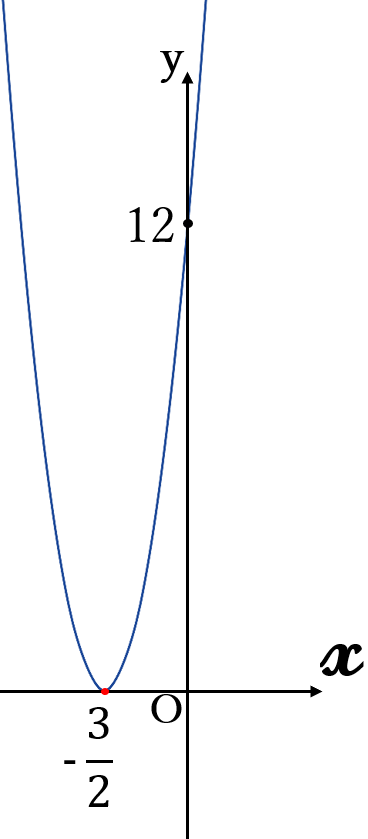
2次方程式
\(4x^2+12x+9=0\)
を解くと
\(4x^2+12x+9\)
\(=(2x+3)^2=0\)
\(2x+3=0\)
\(\large x=-\frac{3}{2}\)
(答) \(\large \left(-\frac{3}{2}, \ 0 \right)\)
例題7
次の2次関数のグラフと\(x\)軸の共有点の個数を求めなさい。
(1) \(\large y=x^2-2x-1\)
(2) \(\large y=2x^2-3x+2\)
(3) \(\large y=-9x^2+6x-1\)
(1)の解答は、少し細かく記述します。
解答
(1) \(\large y=x^2-2x-1\)
与式は \(y=x^2+(-2)x+(-1)\)
\(a=1, \ b=-2, \ c=-1\)
判別式を\( \ D \ \)とすると
\(D=b^2-4ac\)
\(=(-2)^2-4\cdot 1 \cdot (-1)=4+4=8 \gt 0\)
(答) 2個
定期考査では次のように記述すると良いでしょう
解答
(2) \(\large y=2x^2-3x+2\)
判別式を\( \ D \ \)とすると
\(D=(-3)^2-4 \cdot 2 \cdot 2\)
\(=9-16=-7 \lt 0\)
(答) 0個 (共有点はない)
(3) \(\large y=-9x^2+6x-1\)
判別式を\( \ D \ \)とすると
\(D=6^2-4 \cdot (-9) \cdot (-1)\)
\(=36-36=0\)
(答) 1個
練習12
次の2次関数のグラフと\(x\)軸の共有点の個数を求めなさい。
(1) \(\large y=x^2-2x+1\)
(2) \(\large y=-2x^2-3x-1\)
(3) \(\large y=x^2-x+1\)
解答
(1) \(\large y=x^2-2x+1\)
判別式を\( \ D \ \)とすると
\(D=(-2)^2-4 \cdot 1 \cdot 1=4-4=0\)
(答) 1個
(2) \(\large y=-2x^2-3x-1\)
判別式を\( \ D \ \)とすると
\(D=(-3)^2-4 \cdot (-2) \cdot (-1)\)
\(=9-8=1 \gt 0\)
(答) 2個
解答
(3) \(\large y=x^2-x+1\)
判別式を\( \ D \ \)とすると
\(D=(-1)^2-4 \cdot 1 \cdot 1\)
\(=1-4=-3 \lt 0\)
(答) 0個 (共有点はない)
練習13
2次関数\( \ y=-x^2+2x+m \ \)のグラフと\( \ x \ \)軸の共有点の個数は、定数\(m\)の値によってどのように変わるか。
考査では、■色の部分だけ記述すればよいでしょう。
解答
判別式を\( \ D \ \)とすると
\(D=2^2-4 \cdot (-1) \cdot m=4+4m=4(m+1)\)
\(D \gt 0 \ \)のとき、すなわち
\(m+1 \gt 0, \quad m \gt -1 \ \)のとき
求める共有点の個数は、2個
\(D = 0 \ \)のとき、すなわち
\(m+1 = 0, \quad m = -1 \ \)のとき
求める共有点の個数は、1個
\(D \lt 0 \ \)のとき、すなわち
\(m+1 \lt 0, \quad m \lt -1 \ \)のとき
求める共有点の個数は、0個
\(m \gt -1 \ \)のとき、2個
\(m = -1 \ \)のとき、1個
\(m \lt -1 \ \)のとき、0個
