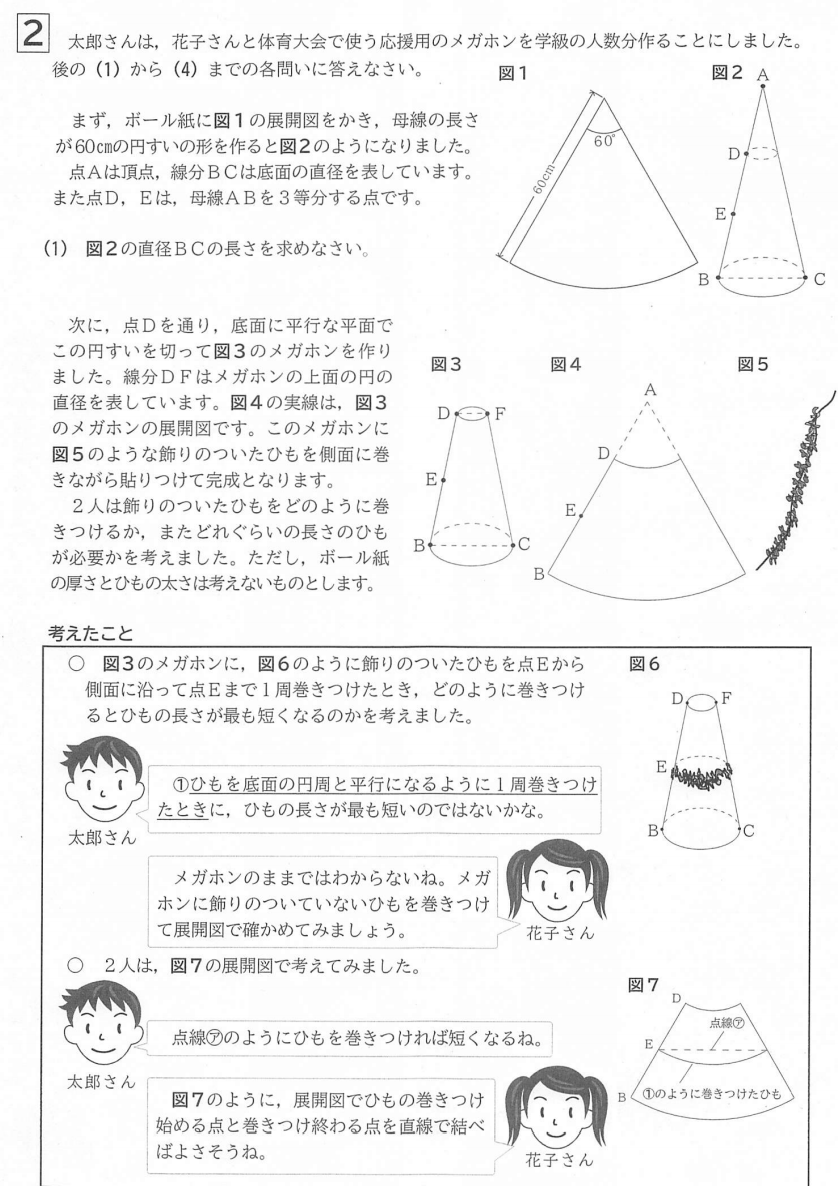
思考を要する図形問題が多く出題されている。
大問2⃣

大問2⃣(3)解答例
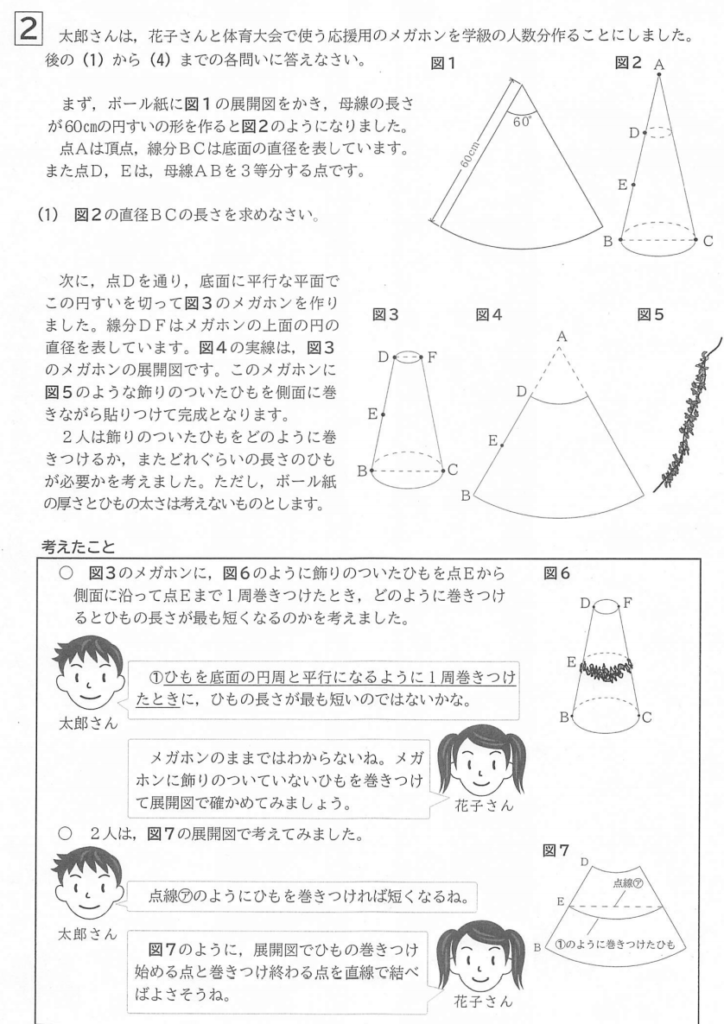
右下の図のように、円錐形を作ったときに点\(D\)と重なる点を\(D’\)とする。
求めるひもの長さは線分\(ED’\)の長さである。
\(\angle EAD’=60^{\circ},AE:AD’=2:1\)だから
\(\triangle AED’\)は
\(\angle ED’A=90^{\circ}\)の直角三角形
よって、\(ED’=20\sqrt{3}\)
(3)(答) \(20\sqrt{3}\) \((cm)\)
(4)解答例
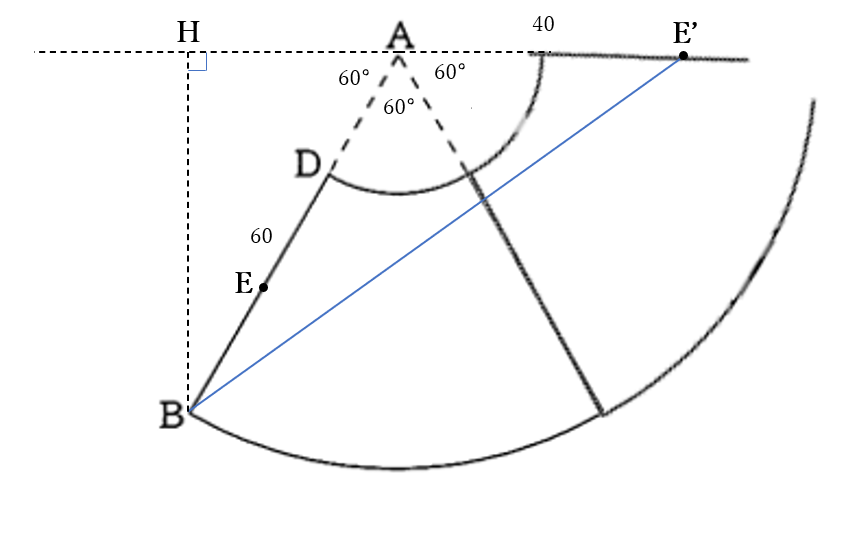
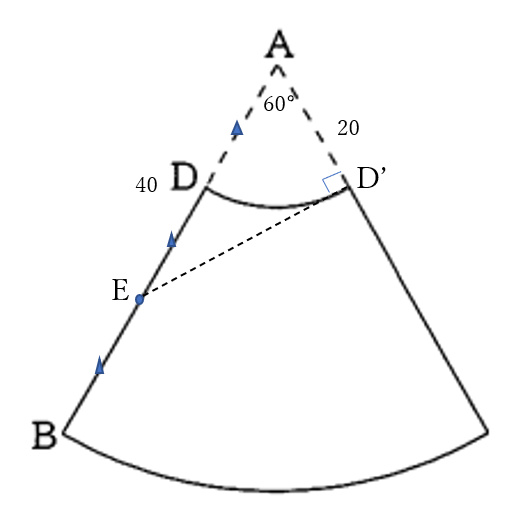
ひもは円錐を2周するので、右下の図のように、扇形を二つ並べた展開図を作る。2周して点\(E\)と重なる点を\(E’\)とする。
求めるひもの長さは、線分\(BE’\)の長さである。
点\(B\)から直線\(AE’\)の延長線に下した垂線の足を\(H\)とする。
\(\triangle BAH\)において
\(\angle BAH=60^{\circ},AB=60\) だから
\(AH=30,BH=30\sqrt{3}\) よって
\(BE=\sqrt{BH^2+HE’^2}\)
\(=\sqrt{(30\sqrt{3})^2+(30+40)^2}\)
\(=\sqrt{2700+4900}=\sqrt{7600}\)
\(=20\sqrt{19}\)
(4)(答) \(20\sqrt{19}\) \((cm)\)
大問4⃣

(3)解答例
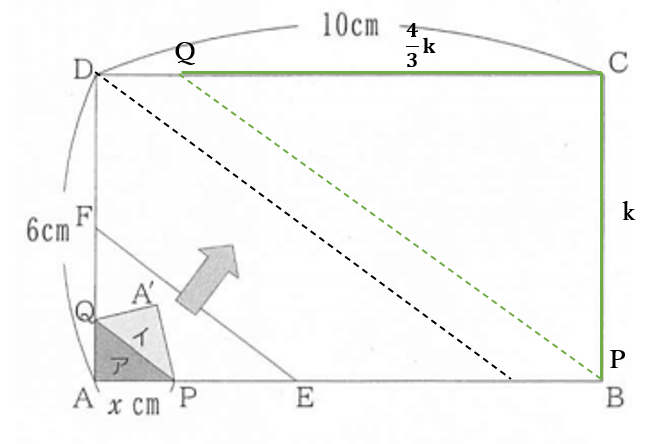
アの面積が長方形\(ABCD\)の面積の\(\frac{5}{8}\)のとき、イの面積は長方形\(ABCD\)の面積の\(\frac{3}{8}\)であるからイの面積は
\(60 \times \frac{3}{8}=\frac{45}{2}\)
ここで \(P\) が \(B\) にあると仮定すると、
\(\triangle AEF \sim \triangle CQP\) だから
\(CP=6,CQ=8\) より \(\triangle CPQ\)の面積は \(24\)
イの面積\(\frac{45}{2}\) は \(\triangle CPQ\)の面積\(24\) より小さいから、\(P\)は辺\(BC\)上にある。
\(CP=k\)とおくと、\(CQ=\frac{4}{3}k\)
したがってイの面積が\(\frac{45}{2}\)になることから
\(\triangle CPQ=k \times \frac{4}{3}k \times \frac{1}{2}=\frac{45}{2}\)
\(\iff \frac{2}{3}k^2=\frac{45}{2}\)
\(\iff k=\frac{3\sqrt{15}}{2}\)
よって求める\(x\)の値は
\(x=16-\frac{3\sqrt{15}}{2}\)
(3) (答) \(16-\large \frac{3\sqrt{15}}{2}\)
(4)解答例
右下の図のように、線分\(QP\)に関して点\(C\)と対称な点を\(C’\)とおくと、点\(C’\)は線分\(AB\)上にある。線分\(CC’\)と線分\(QP\)との交点を\(H\)とおく。
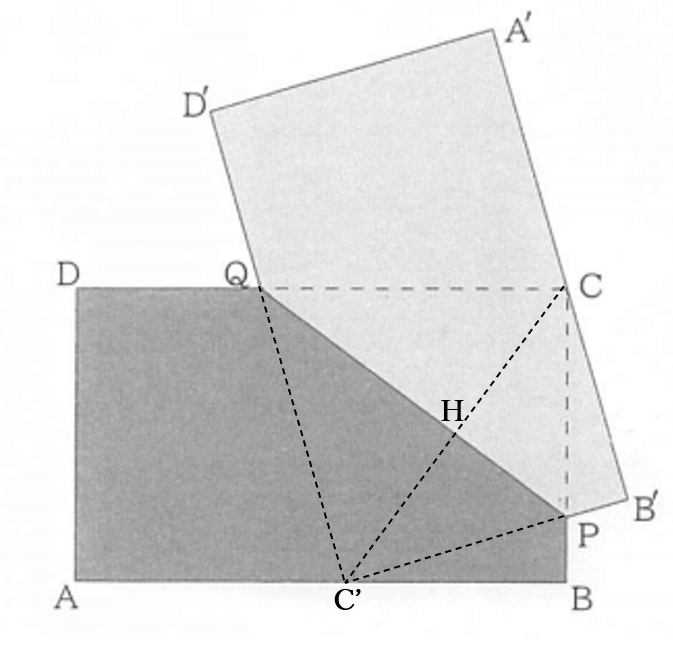
\(\triangle QCP\)において
\(CP:QC:QP=3:4:5\) で
\(\triangle QCP \sim \triangle CBC’ \sim \triangle CHP\) だから
\(CC’=\frac{5}{4}CB=\frac{5}{4} \times 6=\frac{15}{2}\)
よって
\(CP=\frac{5}{4}CH=\frac{5}{4} \cdot \frac{1}{2}CC’\)
\(=\frac{5}{4} \cdot \frac{1}{2} \cdot \frac{15}{2}\)
\(=\frac{75}{16}\)
求める\(x\)の値は
\(x=16-\frac{75}{16}=\frac{181}{16}\)
(4) (答) \(\large \frac{181}{16}\)