全体的に素直で解きやすい問題である。面積体積問題を含めた図形問題が多く出題されている。難解ではないが、時間との戦いなので効率よく解く必要がある。
大問3⃣
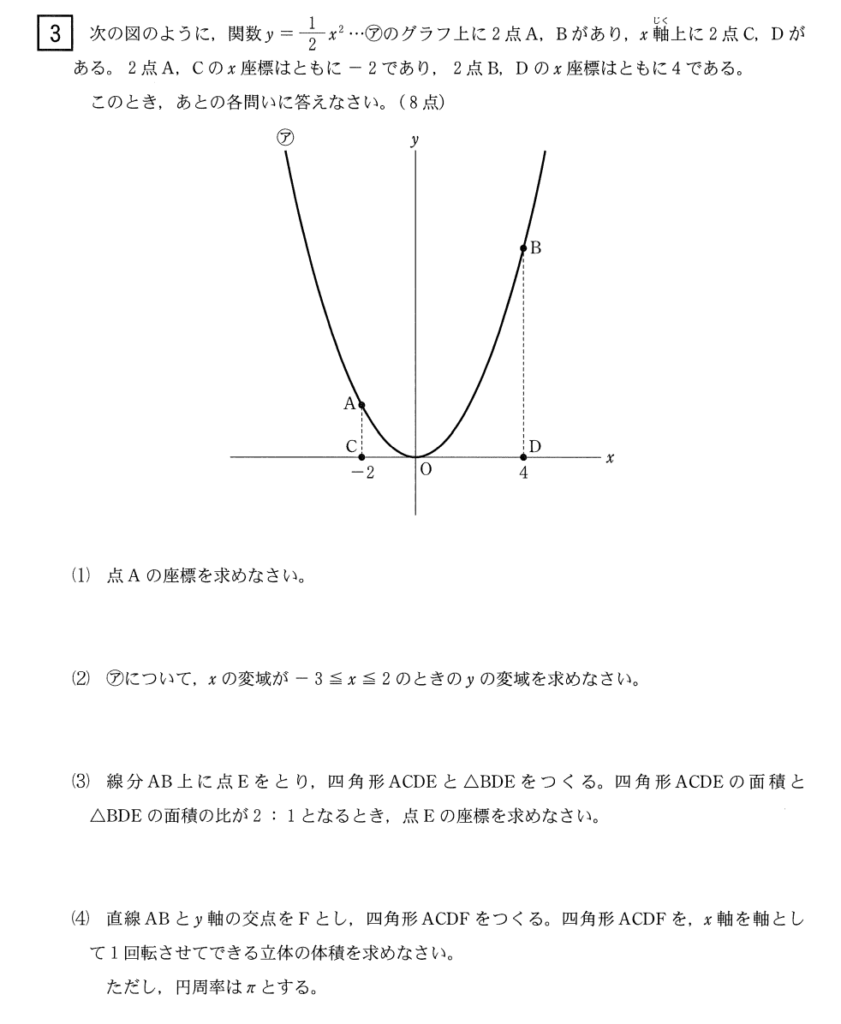
(3)解答例
\(A(-2,2), \quad B(4,8)\)
直線\(AB\)の方程式は
\(y=x+4\)
点\(E\)の\(x\)座標を\(k\)とおく
\(E(k,k+4)\)
四角形\(ACDE\)の面積と\(\triangle BDE\)の面積の比が\(2:1\)ならば
\(\triangle BDE\)の面積は台形\(ACDB\)の面積の\(\frac{1}{3}\)である。
台形\(ACDB\)の面積は
\(\frac{1}{2}\times (2+8)\times 6=30\)
だから
\(\triangle BDE=(4-k)\times 8 \times \frac{1}{2}\)
\(=\frac{1}{3} \times 30\)
\(\iff 4(4-k)=10\)
\(\iff k=\frac{3}{2}\)
よって、点\(E\)の座標は
\(E(\frac{3}{2},\frac{11}{2})\)
(3)(答) \(\large E(\frac{3}{2},\frac{11}{2})\)
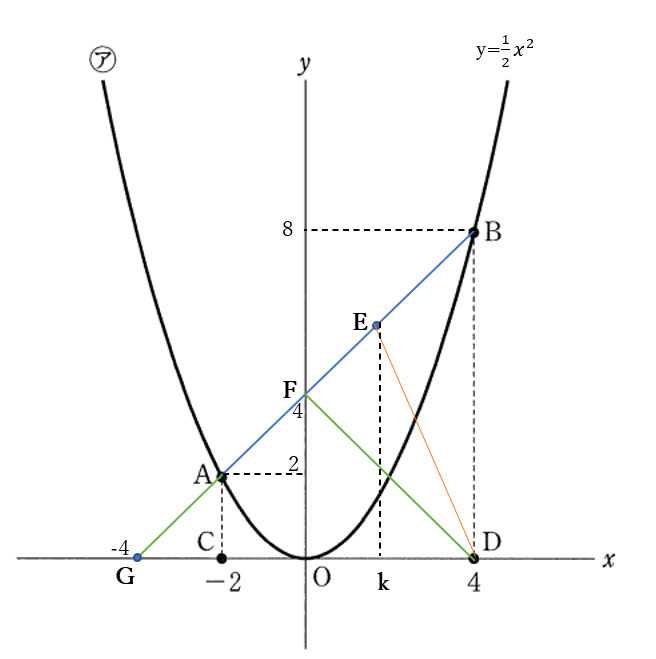
(4)解答例
右の図のように、直線\(AB\)と\(x\)軸との交点を\(G\)とする。
\(G(-4,0), \quad F(0,4)\)
\(\triangle FOD \equiv \triangle FOG\)
\(\triangle FOD \sim \triangle ACG\)
\(\triangle FOD\)と\(\triangle ACG\)の相似比は\(2:1\)
よって求める立体の体積は
円錐形\(FOD\times 2\)
\(-\quad \)円錐形\(FOD \times (\frac{1}{2})^3\)
\(=\)円錐形\(FOD\times (2-\frac{1}{8})\)
\(=\)円錐形\(FOD \times \frac{15}{8}\)
\(=\pi \times 4^2 \times 4 \times \frac{1}{3} \times \frac{15}{8}\)
\(=40\pi\)
(4) (答) \(40\pi\)
大問4⃣
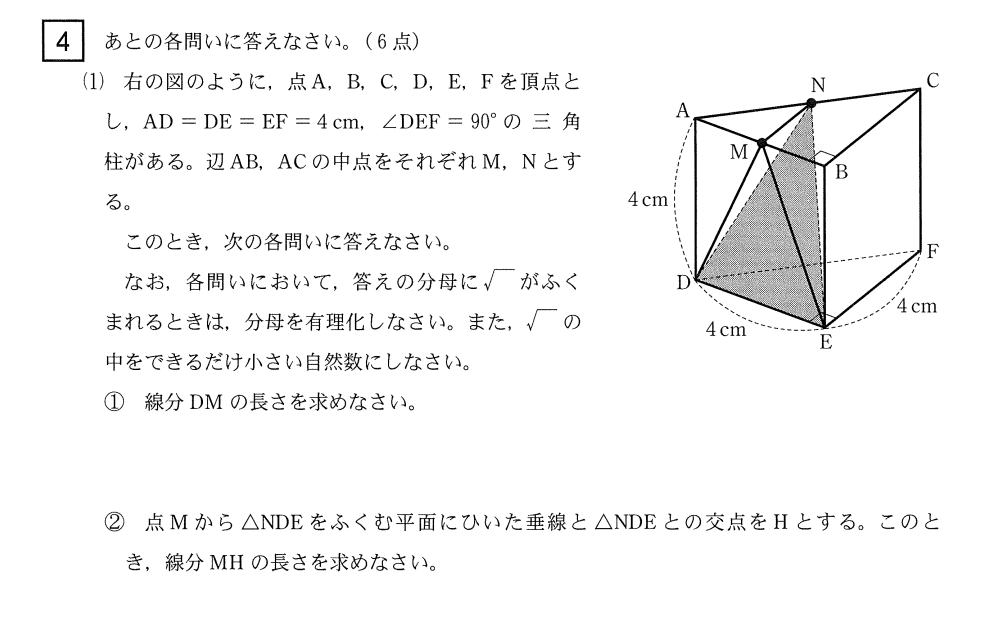
(1)解答例
① \(DM=\sqrt{AD^2+AM^2}\)
\(=\sqrt{4^2+2^2}=2\sqrt{5}\)
① (答) \(2\sqrt{5}\) \((cm)\)
②
三角錐\(N-MDE\)の体積を求める
\(\triangle MDE\)の面積は
\(4\times 4\times \frac{1}{2}=8\)
\(MN=2\) ゆえ、三角錐\(N-MDE\)の体積は
\(8\times 2\times \frac{1}{3}=\frac{16}{3}\cdots (\ast)\)
底面を\(\triangle NDE\)としたときの三角錐\(N-MDE\)の高さは\(MH\)なので
\((\ast)\)と\(\triangle NDE \times MH\times \frac{1}{3}\)
より\(MH\)を求める
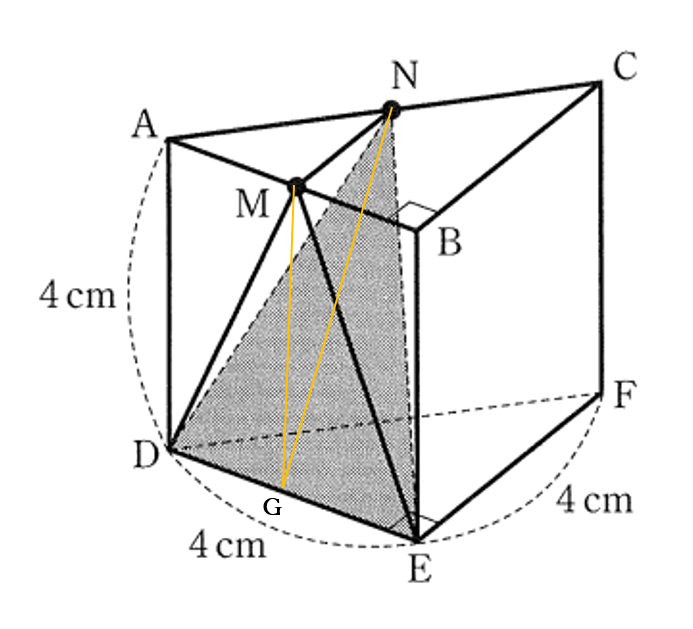
右の図のように、辺\(DE\)の中点を\(G\)とおく
\(NG=\sqrt{MG^2+MN^2}\)
\(=\sqrt{4^2+2^2}=2\sqrt{5}\)
\(\triangle NDE\)の面積は
\(\triangle NDE=DE \times NG \times \frac{1}{2}\)
\(=4\times 2\sqrt{5} \times \frac{1}{2}\)
\(=4\sqrt{5}\)
\((\ast)\)より
\(\triangle NDE \times MH \times \frac{1}{3}=\frac{16}{3}\)
\(\iff 4\sqrt{5}MH=16\)
\(\iff MH=\large \frac{4\sqrt{5}}{5}\)
② (答) \(\large \frac{4\sqrt{5}}{5}\) \((cm)\)
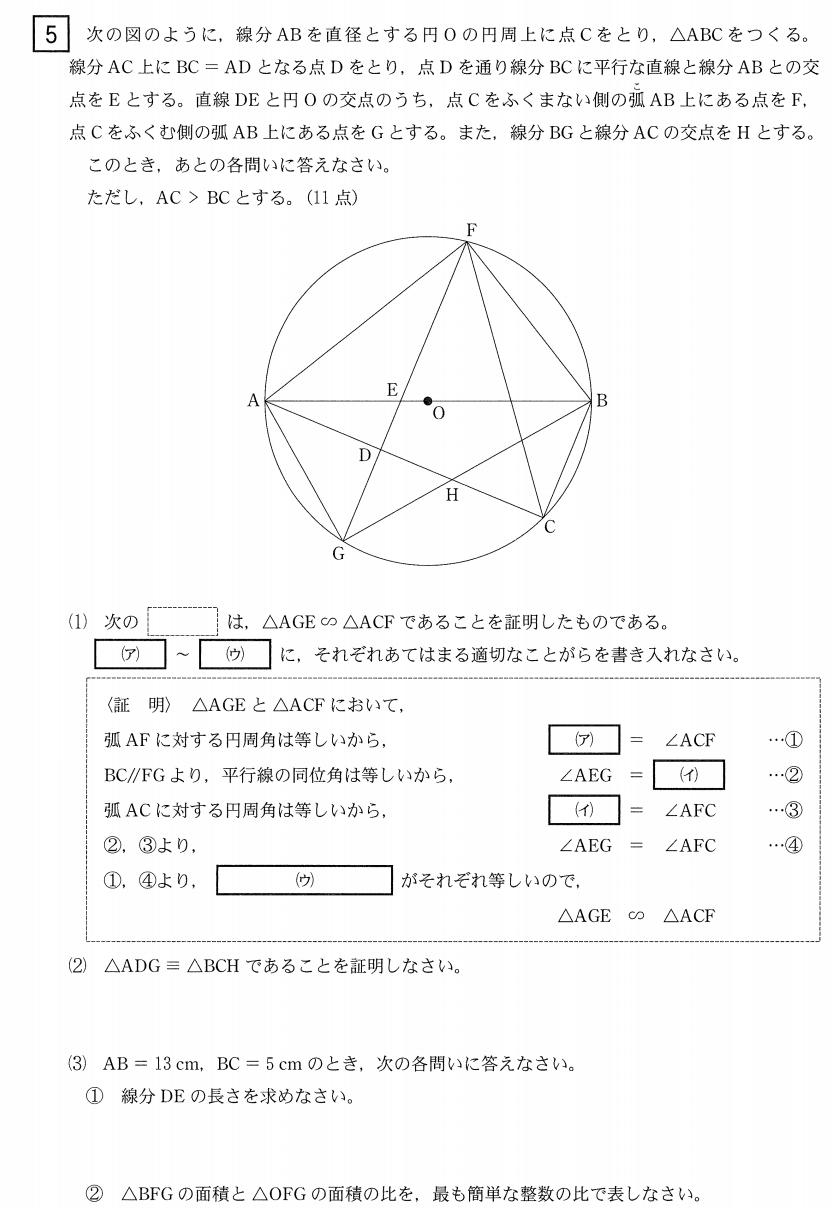
大問5⃣
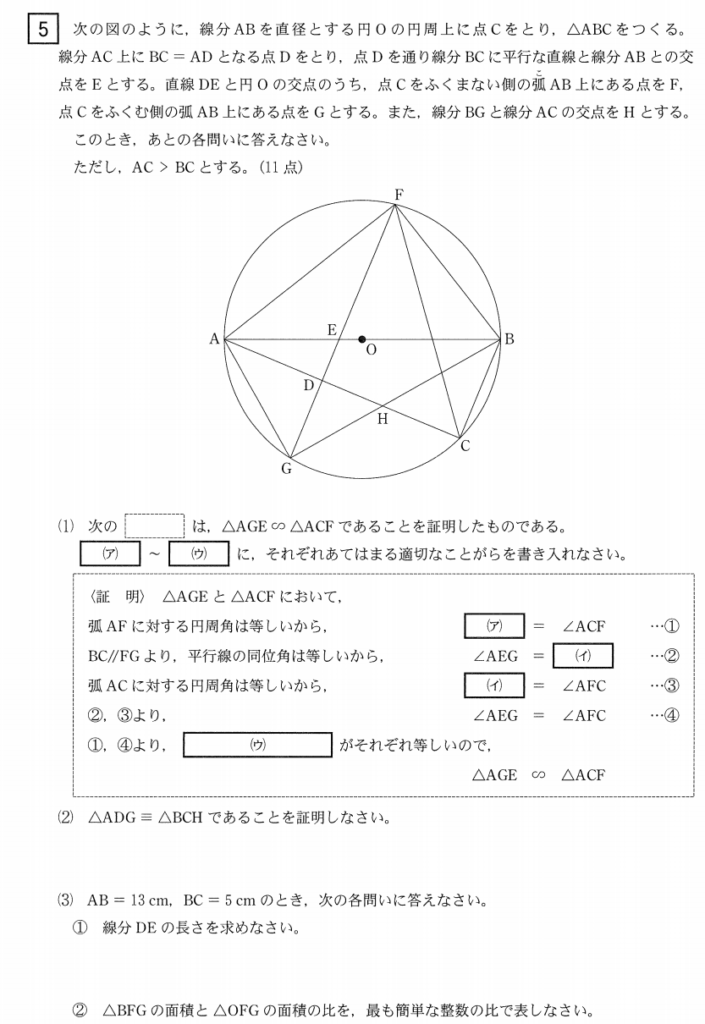
(3)解答例
①
\(\triangle ABC\)は
\(\angle BCA=90^{\circ}\)の直角三角形
\(AC=\sqrt{AB^2-BC^2}\)
\(=\sqrt{13^2-5^2}=\sqrt{144}=12\)
\(\triangle ADE \sim \triangle ACB\)より
\(DE:BC=AD:AC\)
\(\iff DE=\frac{AD}{AC} \times BC=\frac{5}{12} \times 5\)
\(=\frac{25}{12}\)
① (答) \(\large \frac{25}{12}\) \((cm)\)
②
\(AC:AD=12:5\)
\(\iff AB:AE=12:5\)
\(\iff AB:BE=12:7\)
だから
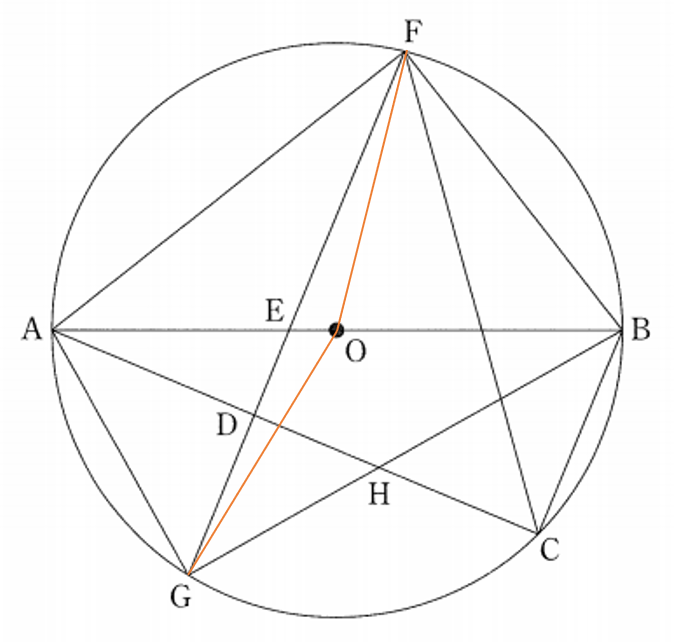
\(\triangle BFG : \triangle OFG=BE:OE\)
\(=\frac{7}{12}AB:(\frac{7}{12}AB-\frac{1}{2}AB)\)
\(=\frac{7}{12}:\frac{1}{12}=7:1\)
② (答) \(\triangle BFG : \triangle OFG \quad =\quad 7:1\)