難解な問題が3題出題されている。大問3(2)②、大問4(2)、大問5(3)である。
とくに規則性の問題・大問5(3)はかなり手ごわいと思われる。限られた時間の中でいったいどれだけの受験生が解答できたのだろうか。
この問題を考察してみよう。


大問5(3)の解答例
各段には連続した自然数が4個ずつ並べられている。したがって、各段には4の倍数が必ず入っていてその4の倍数が各段の最大数である。並べる規則性は問題に書かれているがちょっと解りずらい。
例えば、\(n\)を自然数とすると \(n\)段には、\(4n-3,\) \(4n-2,\) \(4n-1,\) \(4n\) の連続した自然数が与えられた規則に従って並べられている。最大の数は \(4n,\) 最小の数は \(4n-3\)
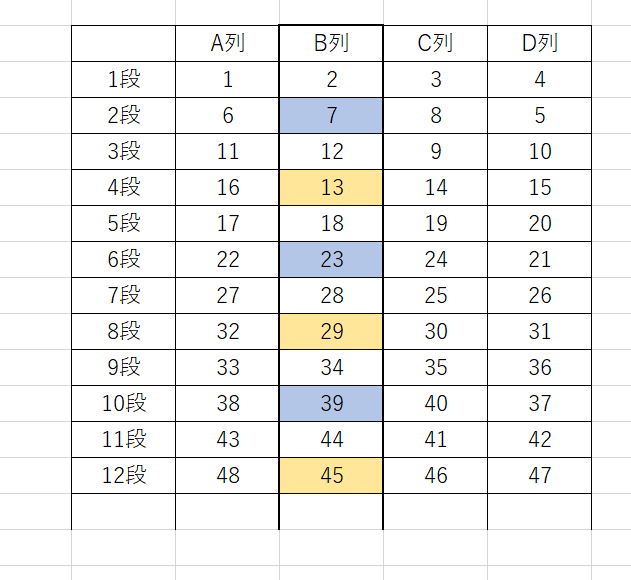
\(m\)段目の最小の数 \(4m-3\)
\(n\)段目の2番目に大きい数 \(4n-1\)
右の表から
\(m=4k,\) \(k=1,2,3, \cdots\)
このとき、\(4m-3\) は\(B\)列
\(m\)は、4の倍数で \(4 \leq m \lt 20\)
\(m=4,8,12,16\) \(\cdots\) ①
\(n=4l-2,\) \(l=1,2,3,4, \cdots\)
このとき、\(4n-1\) は\(B\)列
\(n\)は、4の倍数\(-2\) で \(2 \leq n \lt 20\)
\(n=2,6,10,14,18\) \(\cdots\) ②
この2数の和が12の倍数となることから
\(4m-3+4n-1=12t,\) \(t=1,2,3, \cdots\)
\(\iff 4(m+n-1)=12t\)
\( \iff m+n-1=3t\)
\( \iff m+n=3t+1,\)
\(6 \leq m+n \lt 40\)
よって
\(m+n=7,10,13,16,19,22\)
\(25,28,31,34,37\)
\(m,n\)は偶数だから
\(m+n=10,16,22,28,34\)
さらに\(m+n\)を\(k,l\)で表すと
\(m+n=4k+4l-2=4(k+l)-2\)
だから \(m+n\) は、4の倍数\(-2\)
\(m+n=10,22,34\cdots\)③
①②③より、\(m,n\) の値の組み合わせは
\((m,n)=(4,6),(8,2),(4,18)\)
\((8,14),(12,10),(16,6),(16,18)\)
ゆえに求める組数は、7組 である。・・・(答)
【別解】
単純に数えた方が楽かもしれない。ほとんどの受験生は、19段まで書き出して数えたであろう。\(m,n\)は20未満の自然数だから数えられなくはないが、限られた時間の中で冷静に数えられるかが鍵になる。
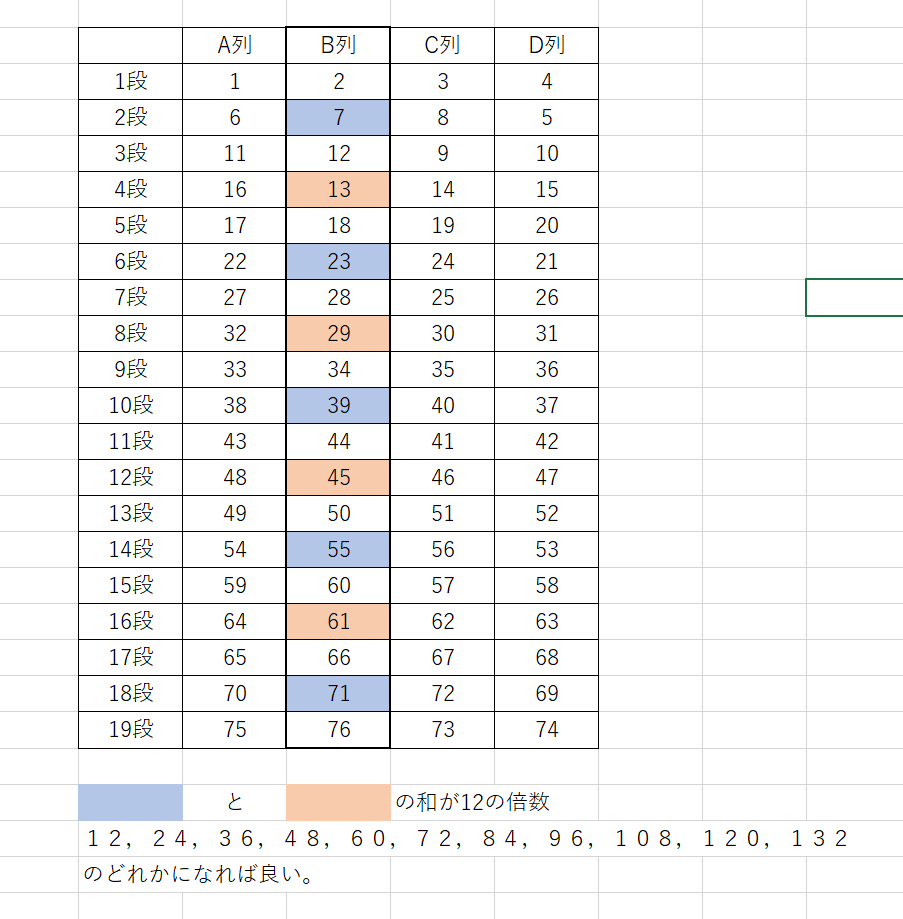
B列にある数 \(4m-3\) は
\(4m-3=13,29,45,61\)
B列にある数 \(4n-1\) は
\(4n-1=7,23,39,55,71\)
この2つの数の和が12の倍数になるものを書き出せばよい。
\(13+23=36,13+71=84\)
\(29+7=36,29+55=84\)
\(45+39=84,61+27=84\)
\(61+71=132\)
以上の7組
次は、大問4(2)である。この問題も時間があれば解けるであろうが、限られた時間の中で、解くことはかなり難しいと思われる。
大問4
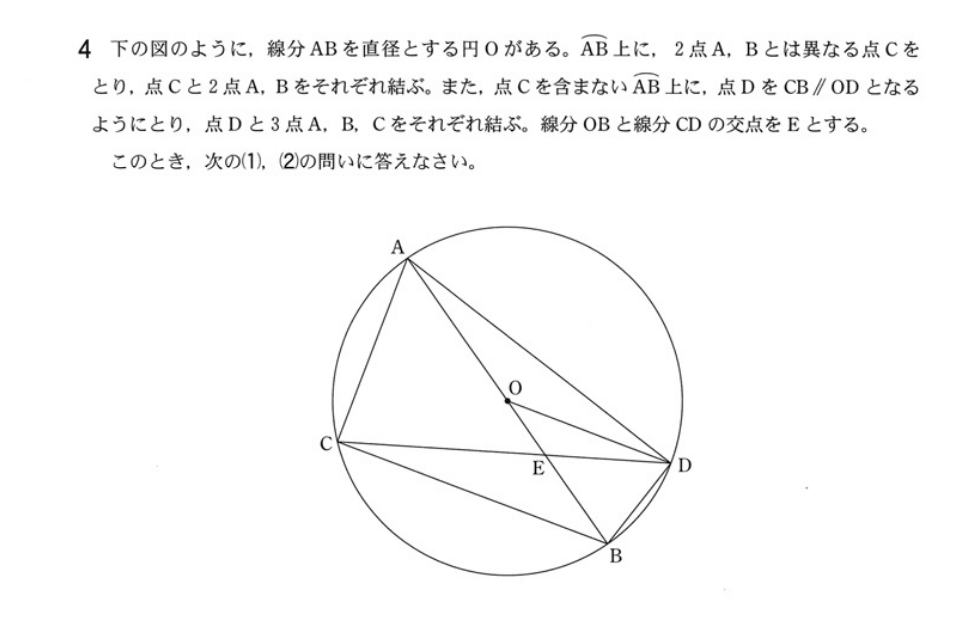

大問4(2)解答例
\(CB/\!/OD\)なので、\(\triangle CBE \sim \triangle DOE\)
よって、\(CB=3,OD=2\) だから
\(CE:DE=BE:OE\)
\(=CB:DO=3:2\)
ゆえに
\(OE=\frac{4}{5},\quad BE=\frac{6}{5}\cdots\)①
\(AE=AO+OE=2+\frac{4}{5}=\frac{14}{5}\)
また、\(CE=t\)とおくと、\(DE= \frac{2}{3} t\)
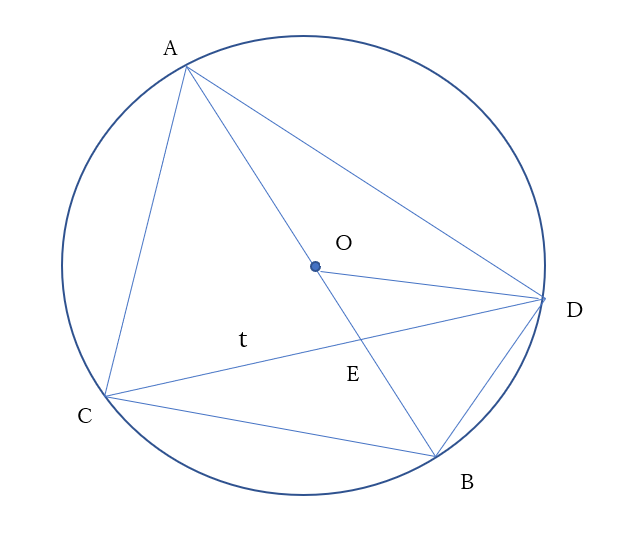
ここで
\(\triangle AEC \sim \triangle DEB\)
だから
\(CE:AE=BE:DE\)
\( \iff t:\frac{14}{5}=\frac{6}{5}:\frac{2}{3}t\)
\(\iff \frac{2}{3}t^2=\frac{14}{5} \times \frac{6}{5}\)
\(\iff t^2=\frac{3^2 \times 14}{5^2}\)
\(\iff t=\frac{3}{5} \sqrt{14}\)
\(\iff CE=\frac{3}{5} \sqrt{14}\cdots\)②
また
\(AC=\sqrt{AB^2-CB^2}\)
\(=\sqrt{4^2-3^2}=\sqrt{7}\cdots\)③
①②③より
\(AC:BD=CE:BE\)
\(\iff \sqrt{7}:BD=\frac{3}{5} \sqrt{14}:\frac{6}{5}\)
\(\iff \frac{3}{5} \sqrt{14}\cdot BD=\frac{6}{5}\sqrt{7}\)
\(\iff BD=\frac{2}{\sqrt{2}}=\sqrt{2}\)
大問4(2) (答) \(\sqrt{2}\) \((cm)\)
それでは、最後に大問3(2)②
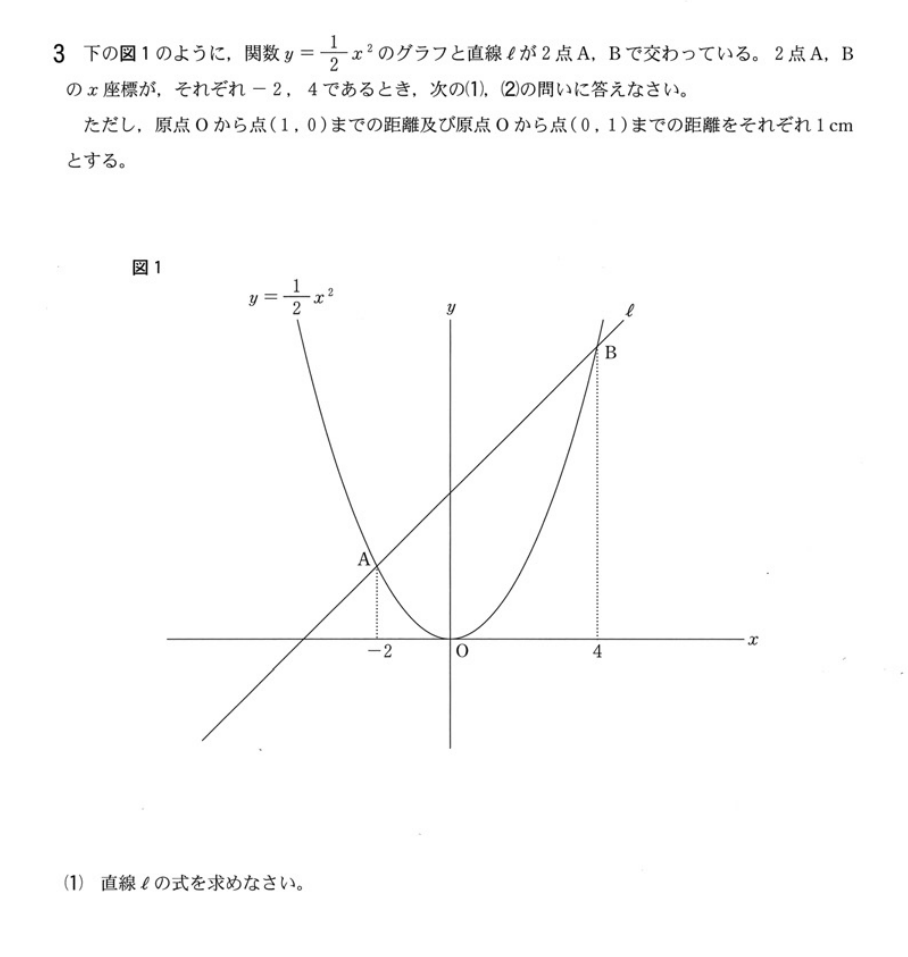
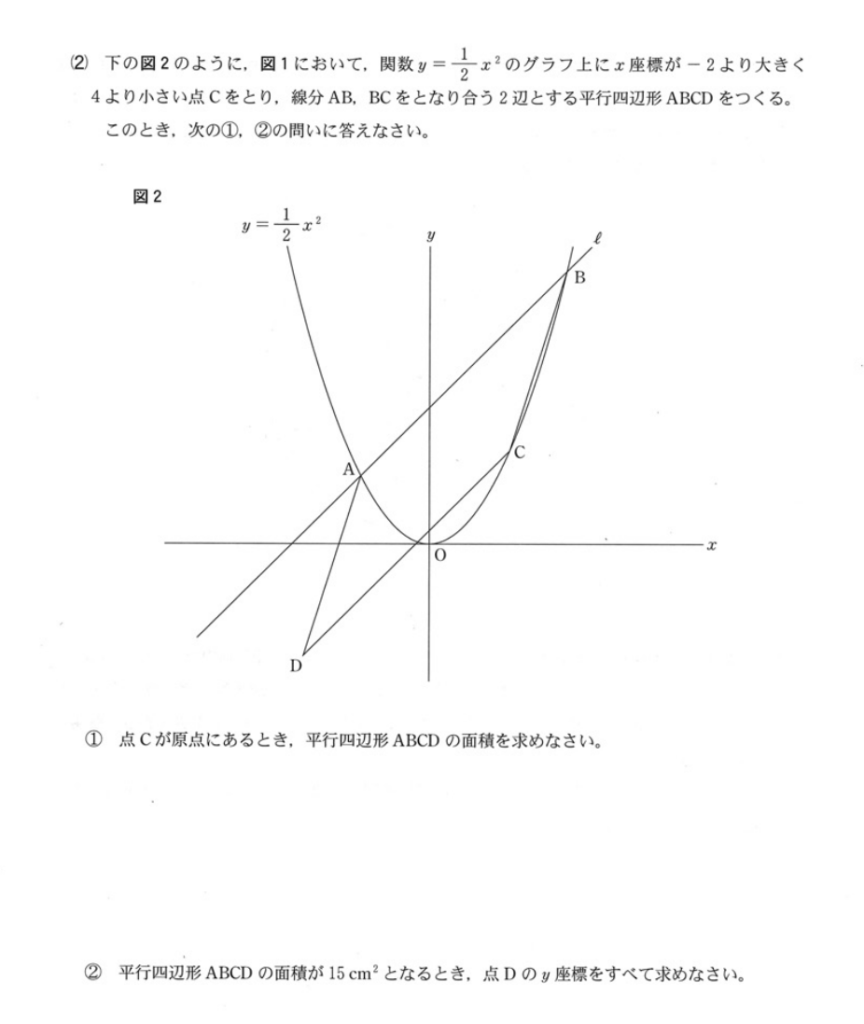
(2)①までに解っていること
放物線 \(y=\frac{1}{2} x^2\) 点\(A(-2,2)\) 点\(B(4,8)\)
直線\(l\) \(y=x+4\)
解答例
点\(C\)の\(x\)座標を\(k\)とおくと、\(C(k,\frac{1}{2}k^2)\)
点\(C\)を通り、\(y\)軸に平行な直線と直線\(l\)との交点を\(E\)、この直線と点\(D\)を通り\(x\)軸に平行な直線との交点を\(G\)とする。
点\(A\)を通り\(x\)軸に平行な直線と、点\(B\)を通り\(y\)軸に平行な直線との交点を\(F\)とする。
\(E(k,k+4)\) \(F(4,2)\)
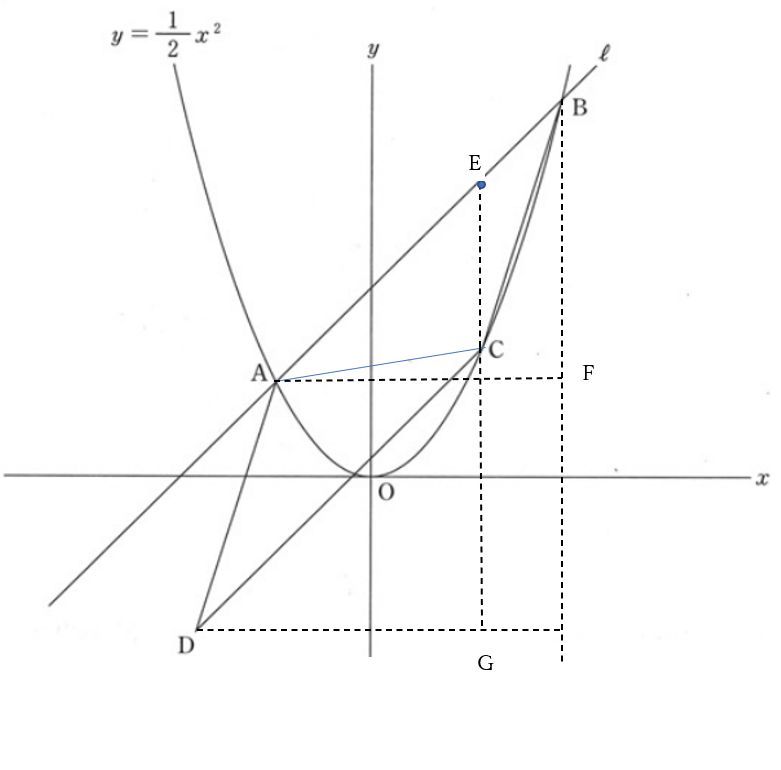
平行四辺形\(ABCD\)の面積は\(\triangle ABC\)の2倍だから
\(\triangle AEC+\triangle BEC=\frac{15}{2}\)
よって \(EC \times AF\)=15
\(((k+4)-\frac{1}{2}k^2) \times (4+2)=15\)
\(\iff k^2-2k-3=0\)
\(\iff (k+1)(k-3)=0\)
\(\iff k=-1,3\)\(\iff C(-1,\frac{1}{2}),(3,\frac{9}{2})\)
\(CG=BF\) だから \(CG=BF=8-2=6\)
よって求める点\(D\)の\(y\)座標は点\(C\)の\(y\)座標から
\(\frac{1}{2}-6,\) \(\frac{9}{2}-6\)
\(\iff -\frac{11}{2},\) \(-\frac{3}{2}\)
(答)\(-\frac{11}{2}\) と \(-\frac{3}{2}\)
