中部地方の府県の入試問題を拝見しているが、令和3年(2021年)の入試問題を公表してない府県が多い。山梨県、新潟県を調べたが、まだ公表されていない(2021年5月4日現在)。愛知県は公表されているので、愛知県の令和3年の高校入試問題を解答してみたい。
愛知県は、入試がAとBの2種類に分類されている。試験問題が異なるが、どうしてこのように分けているのだろう。他県人なので分からない。問題の難易度の差はあまり感じられない。
問題2(1)
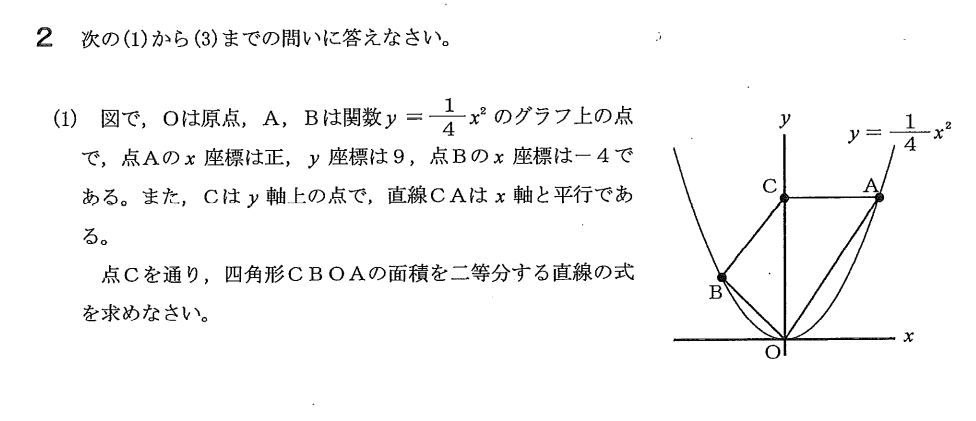
解答例
題意より、
\(A(6,9),B(-4,4),C(0,9)\)
直線\(AO\)の方程式は
\(y=\frac{3}{2}x\)
四角形\(CBOA\)の面積は
\(\triangle CBO+ \triangle ACO\)
\(=9 \times 4 \times \frac{1}{2} + 9 \times 6 \times \frac{1}{2}\)
\(=18+27=45\)
\(\triangle CBO\)の面積よりも\(\triangle ACO\)の面積のほうが大きいので、求める直線は線分\(AO\)と交わる
右下の図のように、線分\(AO\)と求める直線との交点を\(D\)とおくと
四角形\(CBOD=\)四角形\(CBOA \times \frac{1}{2}=\frac{45}{2}\)
\(\iff \triangle CBO + \triangle CDO=\frac{45}{2}\)
\(\iff \triangle CDO=\frac{45}{2}-18=\frac{9}{2}\)
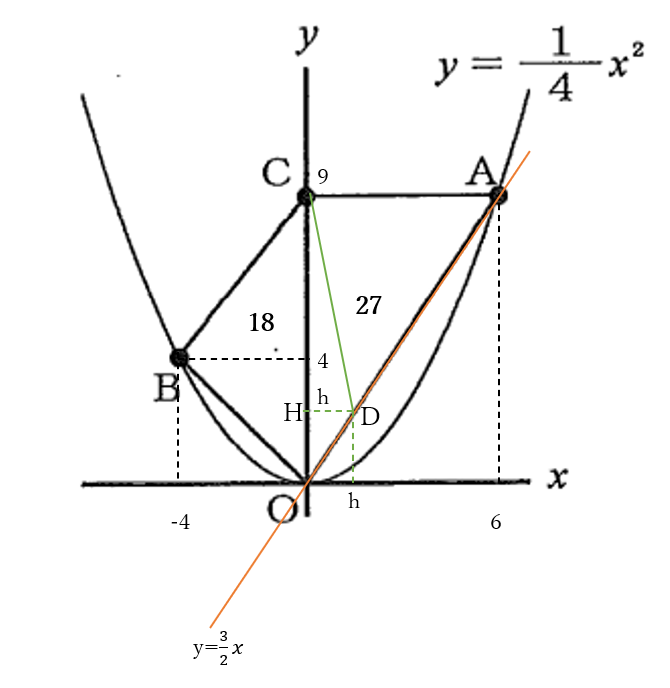
よって、\(\triangle CDO\)の高さを\(h\)とおくと
\(9 \times h \times \frac{1}{2}=\frac{9}{2}\)
\(\iff h=1\)
よって、点\(D\)の座標は\((1,\frac{3}{2})\)
ゆえに求める直線の方程式は
\(y=\large \frac{\frac{3}{2}-9}{1}x+9\)
\(\iff y=-\frac{15}{2}x+9\)
(答) \(y=-\frac{15}{2}x+9\)
問2(3)
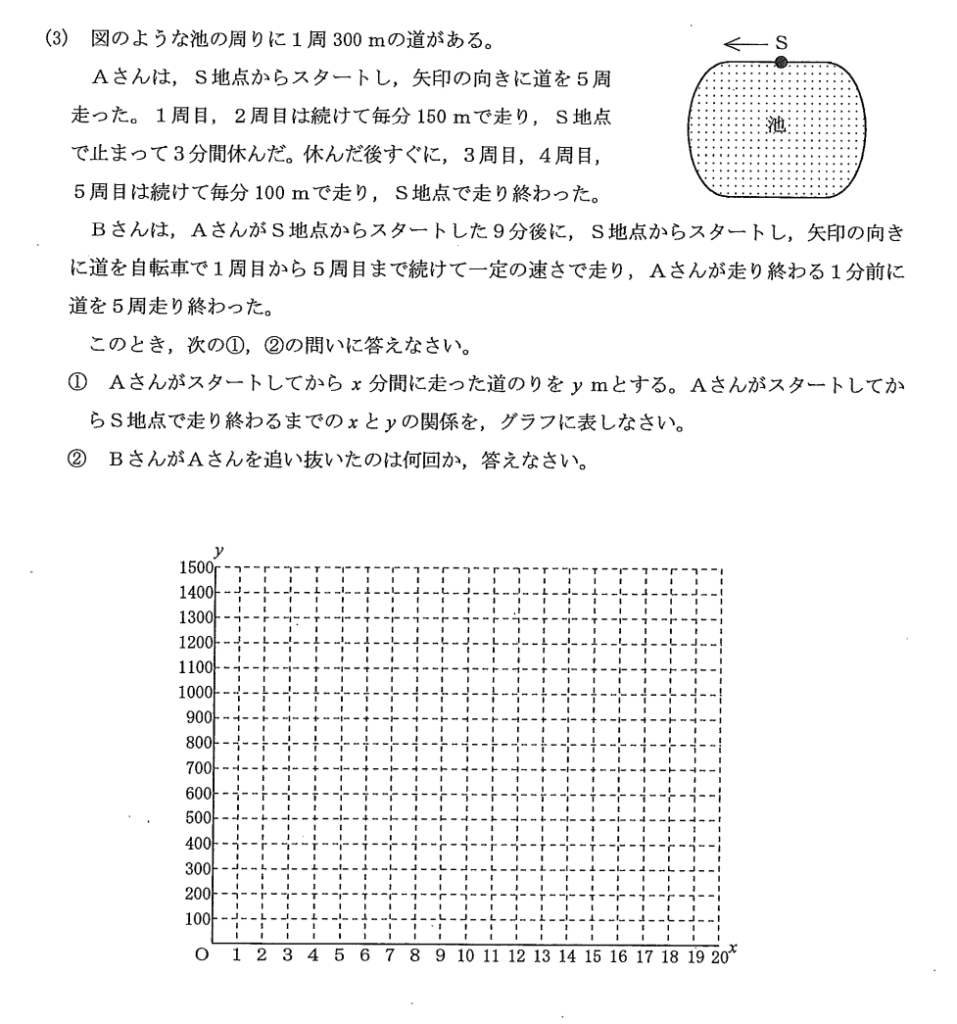
②の解答と説明
\(B\)さんは、6分間で5週\(1500m\)を走ったから、Bさんの速度は
\(\frac{1500}{6}=250(m/分)\)
Bさんが走った6分間でのAさんの走行距離は600mだから、Bさんは、Aさんよりも900m多く走った。これは池3周分の距離であるから、BさんはAさんを3回追い抜いたことになる。
《補足》
BさんはAさんよりも150(m/分)速いから、2分間で、Aさんよりも300m多く走る。1周300mのコースだから、Bさんは、2分間で1回の割合でAさんを追い抜く。Bさんは6分間走ったから、その間にAさんを3回追い抜く。
(答) 3回
問3(2)

解答例
① \(DC=6, \quad DE:EC=2:1\)
より
\(DE=4, \quad EC=2\)
\(EB=\sqrt{BC^2+EC^2}\)
\(=\sqrt{6^2+2^2}=2\sqrt{10}\)
(答) \(2\sqrt{10}\) \((cm)\)
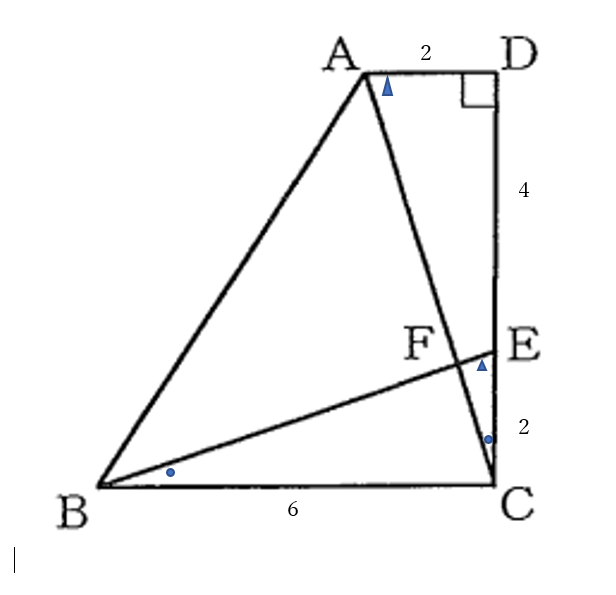
② \(\triangle CAD \equiv \triangle BEC \sim \triangle CEF\)
\(\triangle CAD\)と\(\triangle BEC\)の面積は、ともに\(6\)
\(\triangle BEC\)と\(\triangle CEF\)の相似比は
\(EB:EC=2\sqrt{10}:2=\sqrt{10}:1\)
よって、\(\triangle BEC\)と\(\triangle CEF\)の面積比は
\(\triangle BEC:\triangle CEF\)
\(=(\sqrt{10})^2:1^2=10:1\)
したがって\(\triangle CEF\)の面積は
\(\triangle CEF=\triangle BEC \times \frac{1}{10}\)
\(=6 \times \frac{1}{10}=\frac{3}{5}\)
以上より、求める\(\triangle ABF\)の面積は
\(\triangle ABF\)
\(=\triangle ABC-\triangle BEC+\triangle CEF\)
\(=18-6+\frac{3}{5}=\frac{63}{5}\)
(答) \( \large \frac{63}{5}\) \((cm^2)\)
問3(3)

解答例
① 題意より、
\(\triangle ABE=\frac{9}{35} \triangle ABC\)
\(\iff \triangle ABC \times \frac{3}{5} \times \frac{AE}{AD}\)
\(=\frac{9}{35} \times \triangle ABC\)
\(\iff \frac{AE}{AD}=\frac{9}{35} \times \frac{5}{3}=\frac{3}{7}\)
(答) \(\frac{3}{7}\) 倍
② \(\triangle ADC\)を線分\(AD\)を回転の軸として1回転させてできる立体の体積を\(V1\)とおくと
\(V1=\pi \times 2^2 \times AD \times \frac{1}{3}\)
\(=\frac{4}{3} \pi AD\)
\(\triangle ABE\)を、線分\(AD\)を回転の軸として1回転させてできる立体の体積を\(V2\)とおくと
\(V2=\pi \times 3^2 \times AD \times \frac{1}{3} \times \frac{AE}{AD}\)
\(=3\pi AD \frac{3}{7}=\frac{9}{7} \pi AD\)
よって、求める倍率は
\(\frac{V2}{V1}=\large \frac{\frac{9}{7} \pi AD}{\frac{4}{3} \pi AD}=\frac{27}{28}\)
(答) \(\frac{27}{28}\) 倍
