2次関数の増加減少と
最大値最小値 その3
今までは、2次関数の最大値最小値の基本事項でした。これから、大学入試にもよく出題されている内容になります。
最大値最小値の応用
2次関数のグラフ(放物線)
の頂点の位置が変化する場合
例えば $$ \large y=x^2-2ax (0≦x≦2) $$ \(a \ \)の値によって、グラフ(放物線)の頂点の位置が変化します。したがって、最大値最小値を求める場合、\(a \ \)の値によって場合分けが必要になります。また、その場合分けが、最大値と最小値で異なり、結構複雑です。
例10
では、$$ \large y=x^2-2ax (0≦x≦2) $$ の最小値から調べてみましょう。
この2次関数を、標準形 $$ \large y=a(x-p)^2+q $$ に変形します。$$ \large \begin{eqnarray} y &=& x^2-2ax \\ &=& (x-a)^2-a^2 (0≦x≦2) \end{eqnarray} $$頂点\((a, \ -a^2)\)
軸 \(x=a\) 下に凸
頂点の\( \ x \ \)座標\( \ a \ \)が定義域内にあれば、頂点の\( \ y \ \)座標\( \ -a^2 \ \)が最小値になりますから
(ⅰ) \(0 \ \)≦\( \ a \ \)≦\( \ 2\) のとき
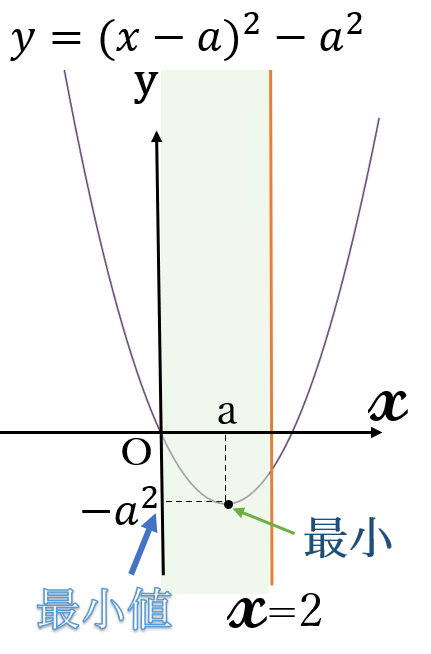
最小値 \(-a^2\) \((x=a)\)
頂点の\( \ x \ \)座標\( \ a \ \)が定義域外にあれば、定義域の端点の\( \ y \ \)座標の小さい方が最小値になります。まずは、頂点の\( \ x \ \)座標\( \ a \ \)が定義域の左側、\( \ 0 \ \)より小さいときを調べます。
(ⅱ) \(a \lt 0 \ \) のとき
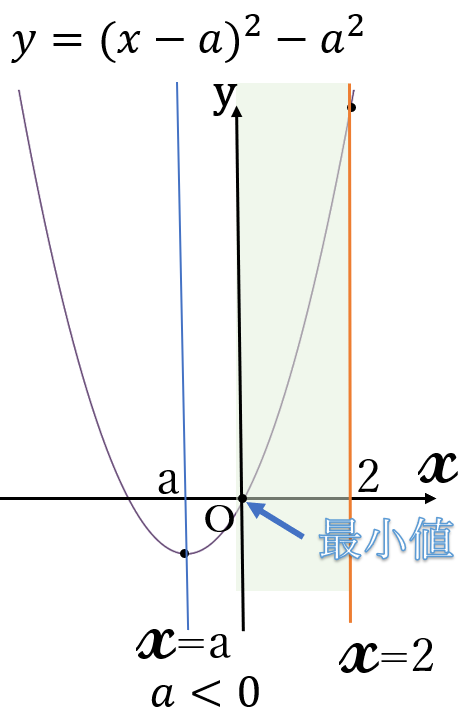
右図のように、定義域の左端(\(x=0 \ \))のとき、グラフは一番下にきます。したがって、\(x=0 \ \)のとき、\(y \ \)の値は最小になります。
\(x=0 \ \)のとき、
\(y=0^2-2a\cdot 0\)
\(=0\)
最小値 \(0\) \((x=0)\)
次は、頂点の\( \ x \ \)座標\( \ a \ \)が定義域の右側、\( \ 2 \ \)より大きいときを調べます。
(ⅲ) \(2 \lt a \ \)のとき
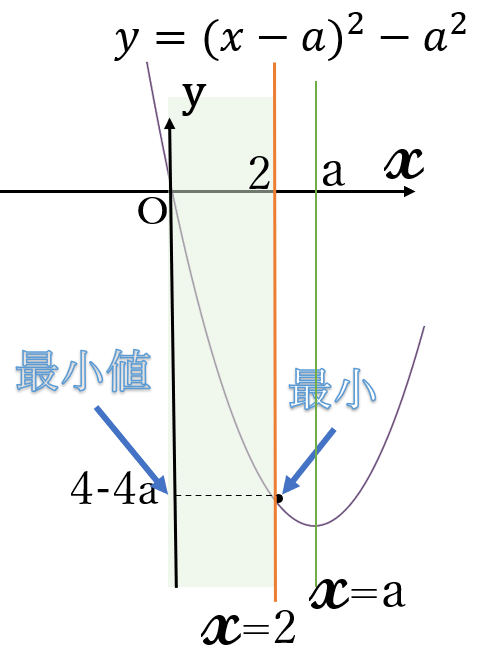
右図のように、定義域の右端(\(x=2 \ \))のとき、グラフは一番下にきます。したがって、\(x=2 \ \)のとき、\(y \ \)の値は最小になります。
\(x=2 \ \)のとき、
\(y=2^2-2a\cdot 2\)
\(=4-4a\)
最小値 \(4-4a\) \((x=2)\)
例10 最小値を\(m(a)\)としてまとめると
\(\begin{eqnarray} m(a) = \begin{cases} 0 & ( a \lt 0 ) \\ -a^2 & ( 0 ≦ a ≦ 2 ) \\ 4-4a & ( a \gt 2 ) \end{cases} \end{eqnarray}\)\( \ \cdots \ \)(答)
例11
では、 $$ y=x^2-2ax (0≦x≦2) $$の最大値です。
最小値と同様に、放物線の頂点と定義域との位置関係で最大値が変わります。しかし、下に凸の放物線ですから、頂点の\( \ y \ \)座標が最大値になることはありません。
下の図を見れば、最大値は、定義域の右端か左端でとることが解ります。したがって、グラフの軸に関する対称性に注目すれば、軸と定義域の中点の左右関係で場合分けをすればよいことになります。
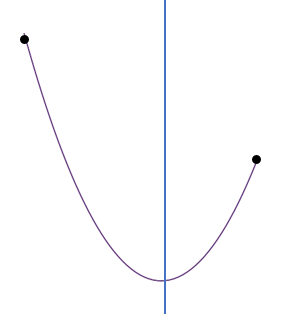
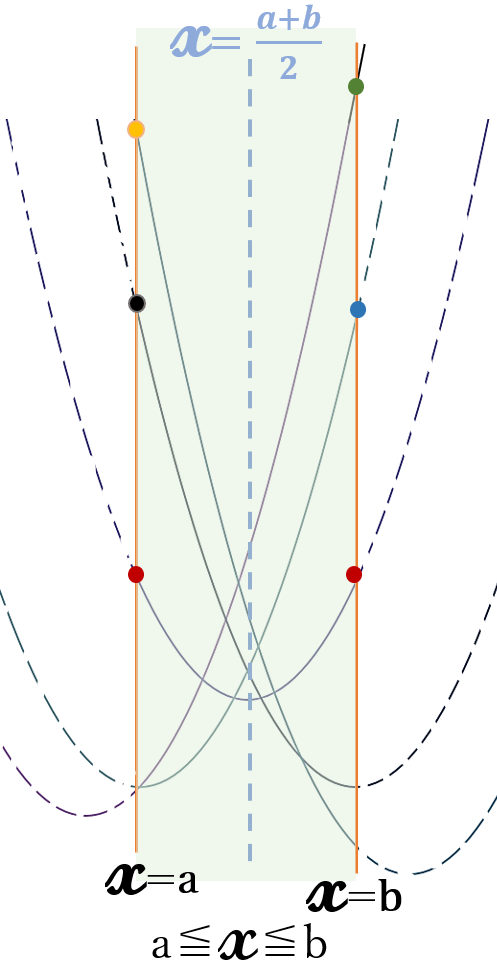
右図のように、定義域の真ん中が、最大値の分かれ目になります。
定義域が、
\(a\)≦\(x\)≦\(b \ \)の場合
放物線の頂点の\( \ x \ \)座標を
\(p \ \)とすると、
\(p\lt \frac{a+b}{2} \ \)のときには
最大値は\( \ x=b \ \)のときになります。
\(\frac{a+b}{2} \lt p \ \)のときには
最大値は\( \ x=a \ \)のときになります。
\(p=\frac{a+b}{2} \ \)のときには
最大値は\( \ x=a=b \ \)のときです。
この2次関数\( \ y=x^2-2ax \ \cdots (\ast) \ \)を、標準形 $$ y=a(x-p)^2+q $$ に変形します。$$ y=x^2-2ax=(x-a)^2-a^2 (0≦x≦2) $$頂点\((a, \ -a^2)\)
軸 \(x=a\)
(ⅰ) \(a \ \lt \ 1 \ \) のとき
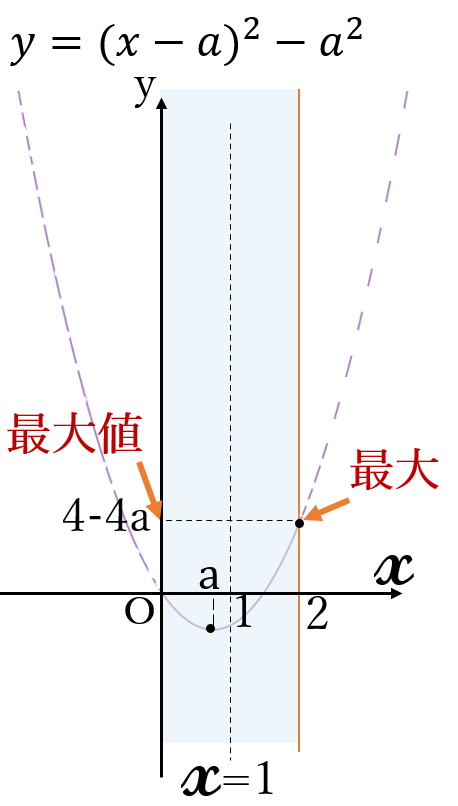
\(x=2 \ \)のとき、
最大となり、
\(y=2^2-2a\cdot 2\)
\(=4-4a\)
最大値 \(4-4a\) \((x=2)\)
(ⅱ) \(1 \ \lt \ a \ \) のとき
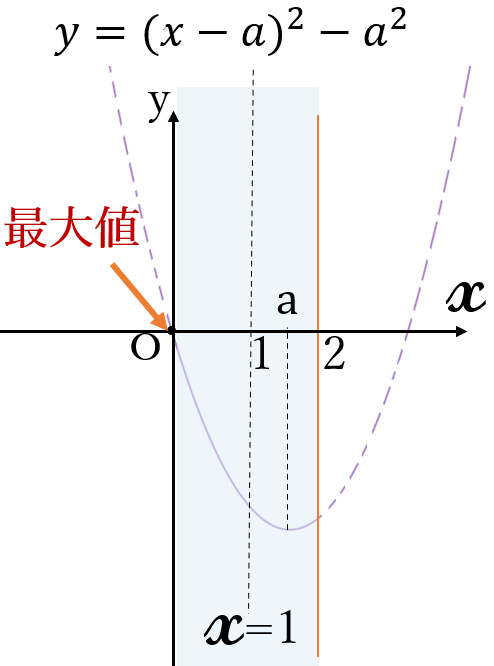
\(x=0 \ \)のとき、
最大となり、
\(y=0^2-2a\cdot 0\)
\(=0\)
最大値 \(0\) \((x=0)\)
(ⅲ) \(a=1 \ \) のとき
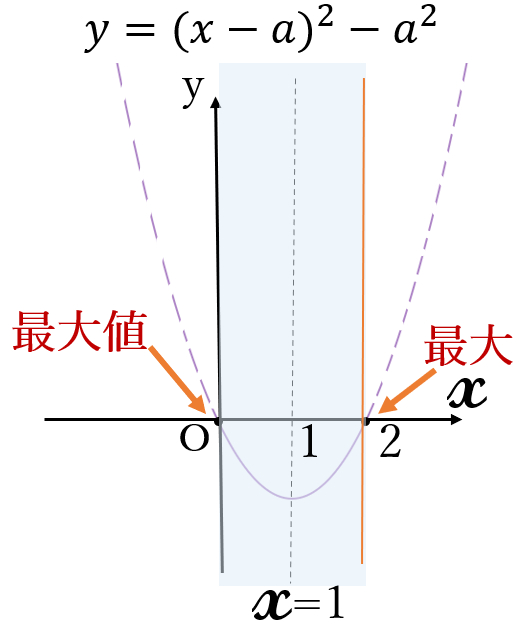
\((\ast) \ \)は、
\(y=x^2-2x\)
\(=(x-1)^2-1\)
頂点 \((1, \ -1)\)
軸 \(x=1\)
また、\((\ast) \ \)は、
\(y=x^2-2x\)
\(=x(x-2) \ \)
となり、
\(x \ \)軸との交点の座標は
\((0, \ 0), \ (2, \ 0) \ \)
よって、最大値は
最大値 \(0\) \((x=0, \ 2)\)
例11 最大値を\(M(a)\)としてまとめると
\(\begin{eqnarray} M(a) = \begin{cases} 4-4a & ( a \lt 1 ) \\ 0 & ( a ≧ 1 ) \end{cases} \end{eqnarray}\)\( \ \cdots \ \)(答)
例10、例11は、2次関数のグラフが、下に凸の放物線でした。上に凸の放物線の場合は、最大値最小値が逆になりますから、例10、例11とは、場合分けも逆になります。
練習6
2次関数 $$ \large y=x^2-4ax+4a^2+3 (-2≦x≦6) $$の最小値を求めなさい。
解答
\(\large y=x^2-4ax+4a^2+3\)
\(\large =(x-2a)^2-4a^2+4a^2+3\)
\(\large =(x-2a)^2+3 (-2≦x≦6)\)
頂点\( \ (2a, \ 3)\) 下に凸
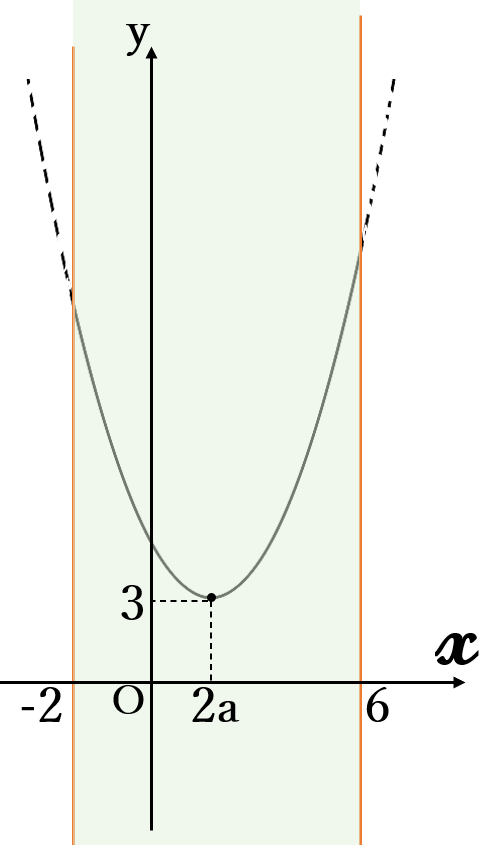
(ⅰ) \(-2 \ \)≦\( \ 2a \ \)≦\( \ 6\)
のとき、
すなわち
\(-1 \ \)≦\( \ a \ \)≦\( \ 3\)
のとき
最小値 \(3\) \((x=2a)\)
頂点の\( \ x \ \)座標\( \ 2a \ \)が定義域外にあれば、定義域の端点の\( \ y \ \)座標の小さい方が最小値になります。まずは、頂点の\( \ x \ \)座標\( \ 2a \ \)が定義域の左側、\( \ -2 \ \)より小さいときを調べます。
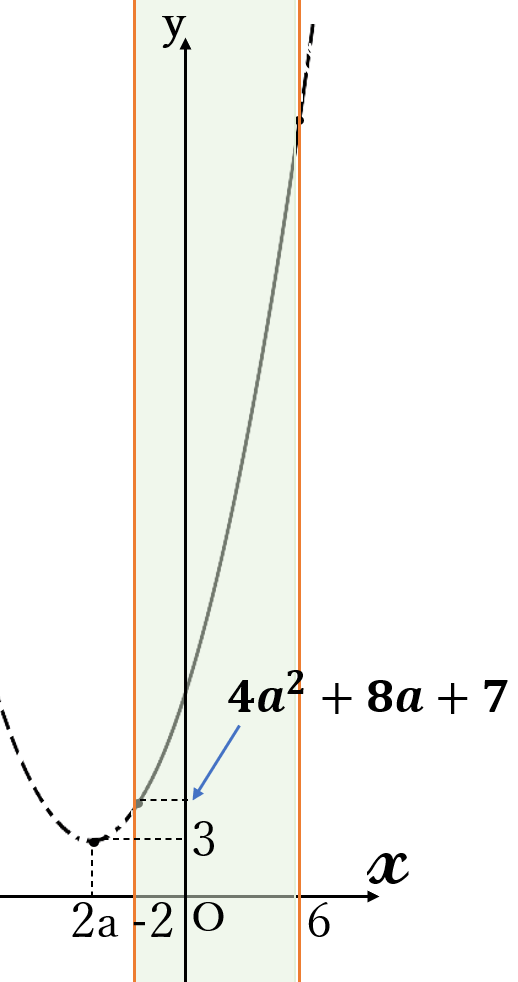
(ⅱ) \(2a \lt -2 \ \)のとき
すなわち
\( \ a \lt -1 \ \)のとき
右図のように、定義域の左端(\(x=-2 \ \))のとき、グラフは一番下にきます。したがって、\(x=-2 \ \)のとき、\(y \ \)の値は最小になります。
\(x=-2 \ \)のとき、
\(y=(-2)^2-4a\cdot (-2)\)
\(+4a^2+3\)
\(=4a^2+8a+7\)
最小値 \(4a^2+8a+7\)
\((x=-2)\)
次は、頂点の\( \ x \ \)座標\( \ 2a \ \)が定義域の右側、\( \ 6 \ \)より大きいときを調べます。
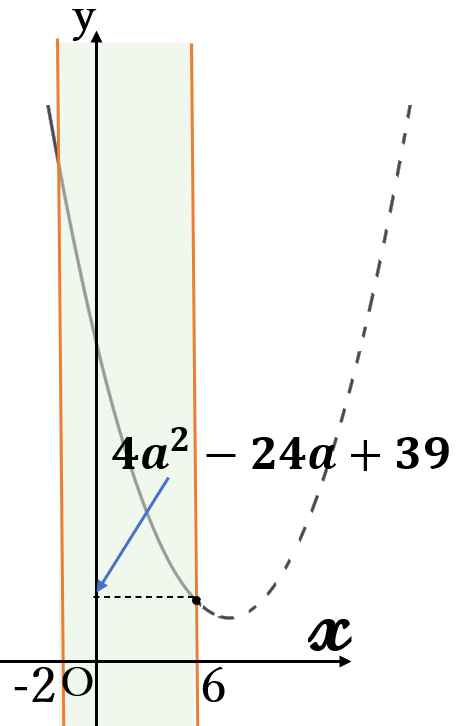
(ⅲ) \(6 \lt 2a \ \)のとき
すなわち
\(3 \lt a \ \)のとき
右図のように、定義域の右端(\(x=6 \ \))のとき、グラフは一番下にきます。したがって、\(x=6 \ \)のとき、\(y \ \)の値は最小になります。
\(x=6 \ \)のとき、
\(y=6^2-4a \cdot 6\)
\(+4a^2+3\)
\(=4a^2-24a+39\)
最小値 \(4a^2-24a+39\) \((x=6)\)
練習6 最小値を\(m(a)\)としてまとめると
\(\begin{eqnarray} m(a) = \begin{cases} 4a^2+8a+7 & ( a \lt -1 ) \\ 3 & ( -1 ≦ a ≦ 3 ) \\ 4a^2-24a+39 & ( a \gt 3 ) \end{cases} \end{eqnarray}\)
\( \ \cdots \ \)(答)
練習7
2次関数 $$ \large y=2x^2-4ax+2a^2-5 (0≦x≦4) $$の最大値を求めなさい。
解答
\(y=2x^2-4ax+2a^2-5\)
\(=2(x^2-2ax)+2a^2-5\)
\(=2\{(x-a)^2-a^2\}+2a^2-5\)
\(=2(x-a)^2-5 (0≦x≦4) \ \cdots \ (\ast)\)
頂点\((a, \ -5)\)
軸 \(x=a\)
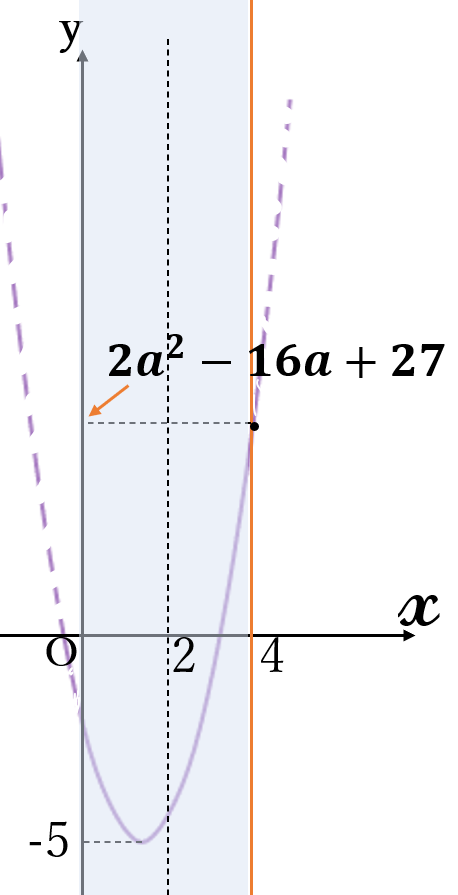
(ⅰ) \(a \lt 2 \ \)のとき
\(x=4 \ \)のとき
\((\ast)\)は最大となり
最大値は
\(y=2 \cdot 4^2-4a \cdot 4\)
\(+2a^2-5\)
\(=2a^2-16a+27\)
最大値\( \ 2a^2-16a+27\)
\((x=4)\)
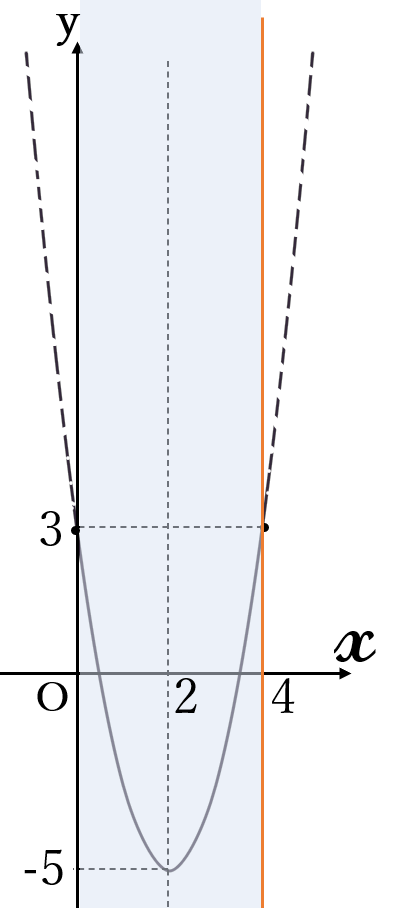
(ⅱ) \(a=2 \ \)のとき
\(x=0, \ 4 \ \)のとき
\((\ast)\)は最大となり
最大値は
\(y=3\)
最大値\( \ 3 \ \) \((x=0, \ 4)\)
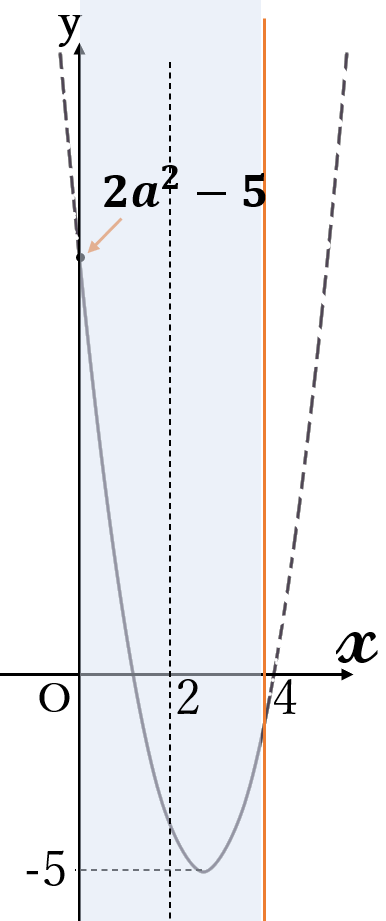
(ⅲ) \(a \gt 2 \ \)のとき
\(x=0 \ \)のとき
\((\ast)\)は最大となり
最大値は
\(y=2a^2-5\)
最大値 \(2a^2-5\)
\((x=0)\)
練習7 最大値を\(M(a)\)としてまとめると
\(\begin{eqnarray} M(a) = \begin{cases} 2a^2-16a+27 & ( a \lt 1 ) \\ 2a^2-5 & ( a ≧ 1 ) \end{cases} \end{eqnarray}\)
\( \ \cdots \ \)(答)
2次関数のグラフ(放物線)
の定義域が変化する場合
例えば $$ \large y=x^2-4x (a≦x≦a+2) $$ \(a \ \)の値によって、定義域が変化します。したがって、最大値最小値を求める場合、\(a \ \)の値によって場合分けが必要になります。これもまた、最大値と最小値で場合分けが異なり、結構複雑になります。
例12
では、$$ y=x^2-4x (a≦x≦a+2) $$ の最小値から
この2次関数を、標準形 $$ y=a(x-p)^2+q $$ に変形します。$$ y=x^2-4x=(x-2)^2-4 (a≦x≦a+2) $$頂点\((2, \ -4)\)
軸 \(x=2\)
\(y=x^2-4x=(x-2)^2-4\) \((a≦x≦a+2)\)
頂点\((2, \ -4)\)、軸\( \ x=2 \ \)
頂点の\( \ x \ \)座標\( \ 2 \ \)が定義域内にあれば、頂点の\( \ y \ \)座標\( \ -4 \ \)が最小値になりますから
(ⅰ) \(a \ \)≦\( \ 2 \ \)≦\( \ a+2\) のとき
すなわち \(0 \ \)≦\( \ a \ \)≦\( \ 2\) のとき
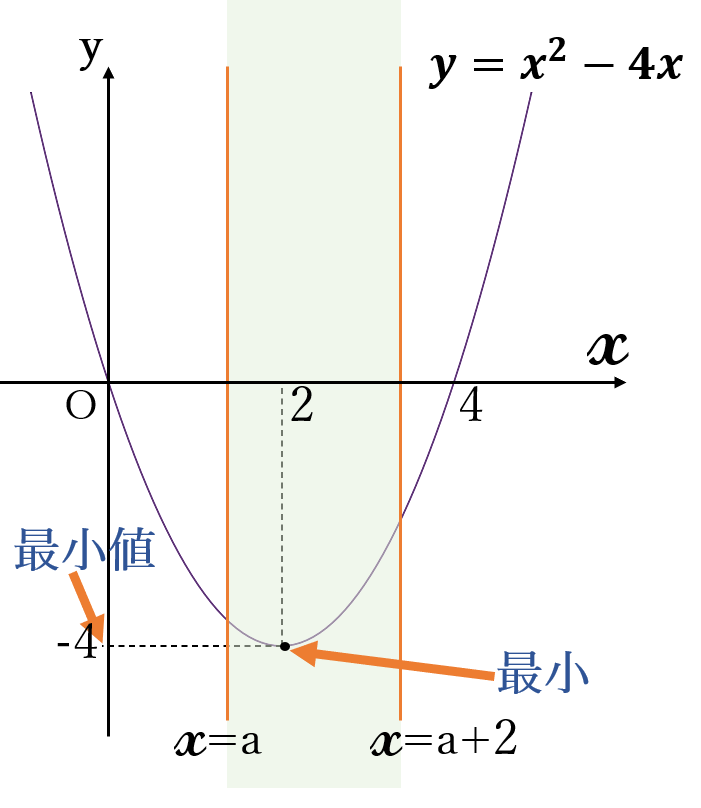
最小値 \(-4\) \((x=2)\)
\(y=x^2-4x=(x-2)^2-4\) \((a≦x≦a+2)\)
頂点\((2, \ -4)\)、軸\( \ x=2 \ \)
頂点の\( \ x \ \)座標\( \ 2 \ \)が定義域外にあれば、定義域の端点の\( \ y \ \)座標の小さい方が最小値になります。まずは、定義域の左側\( \ a \ \)が、頂点の\( \ x \ \)座標\( \ 2 \ \)より大きいときを調べます。
(ⅱ) \(2 \lt a \ \) のとき
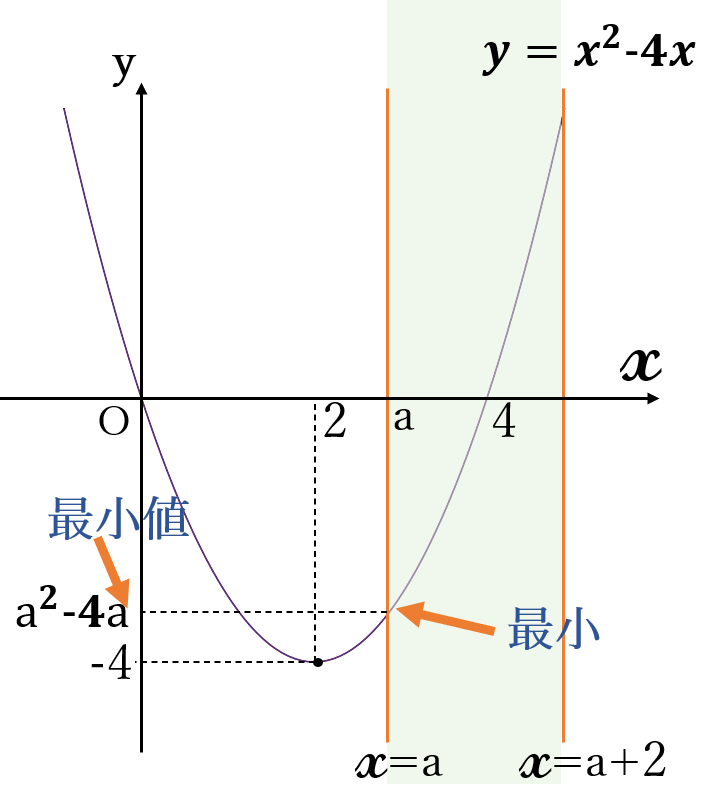
右図のように、定義域の左端(\(x=a \ \))のとき、グラフは一番下にきます。したがって、\(x=a \ \)のとき、\(y \ \)の値は最小になります。
\(x=a \ \)のとき、
\(y=a^2-4a\)
最小値 \(a^2-4a\) \((x=a)\)
\(y=x^2-4x=(x-2)^2-4\) \((a≦x≦a+2)\)
頂点\((2, \ -4)\)、軸\( \ x=2 \ \)
次は、定義域の右側\( \ a+2 \ \)が、\( \ 2 \ \)より小さいときを調べます。
(ⅲ) \(a+2 \lt 2 \ \)のとき、すなわち \(a \lt 0 \ \)のとき
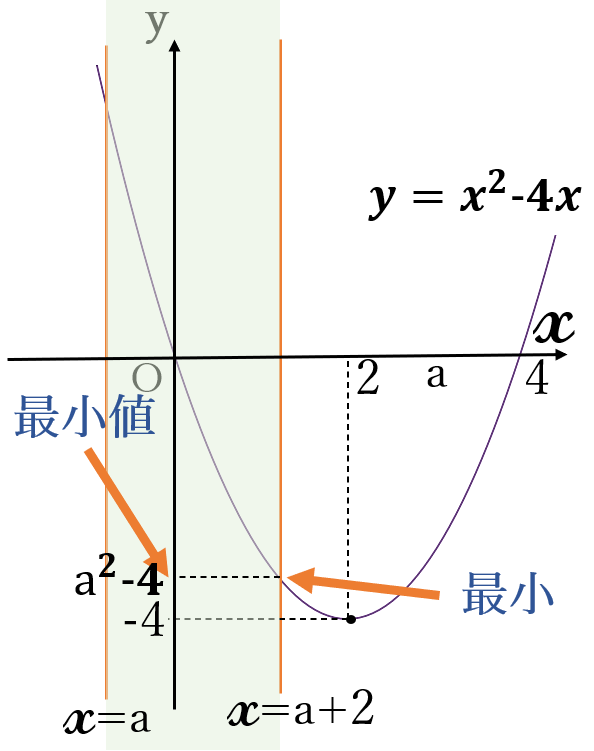
右図のように、定義域の右端、(\(x=a+2 \ \))のとき、グラフは一番下にきます。したがって、\(x=a+2 \ \)のとき、\(y \ \)の値は最小になります。
\(x=a+2 \ \)のとき、
\(y=(a+2)^2-4(a+2)\)
\(=a^2-4\)
最小値 \(a^2-4\) \((x=a+2)\)
\(y=x^2-4x=(x-2)^2-4\) \((a≦x≦a+2)\)
頂点\((2, \ -4)\)、軸\( \ x=2 \ \)
例12 最小値を\(m(a)\)としてまとめると
\(\begin{eqnarray} m(a) = \begin{cases} a^2-4 & ( a \lt 0 ) \\ -4 & ( 0 ≦ a ≦ 2 ) \\ a^2-4a & ( a \gt 2 ) \end{cases} \end{eqnarray}\)\( \ \cdots \ \)(答)
例13
次は、\( y=x^2-4x (a≦x≦a+2) \) の最大値
標準形 \( y=a(x-p)^2+q \) に変形 $$ y=x^2-4x=(x-2)^2-4 (a≦x≦a+2) $$頂点\((2, \ -4)\)
軸 \(x=2\)
例11と同様、最大値は、定義域の右端か左端でとります。軸と定義域の中点の左右関係で場合分けをします。


\(y=x^2-4x=(x-2)^2-4\) \((a≦x≦a+2)\)
頂点\((2, \ -4)\)、軸\( \ x=2 \ \)
定義域\( \ a≦x≦a+2 \ \)の中点は、\(\large \frac{a+a+2}{2}\)\( =a+1 \ \)です。
(ⅰ) \(a+1 ≧ 2 \ \)すなわち\( \ a ≧ 1 \ \)のとき
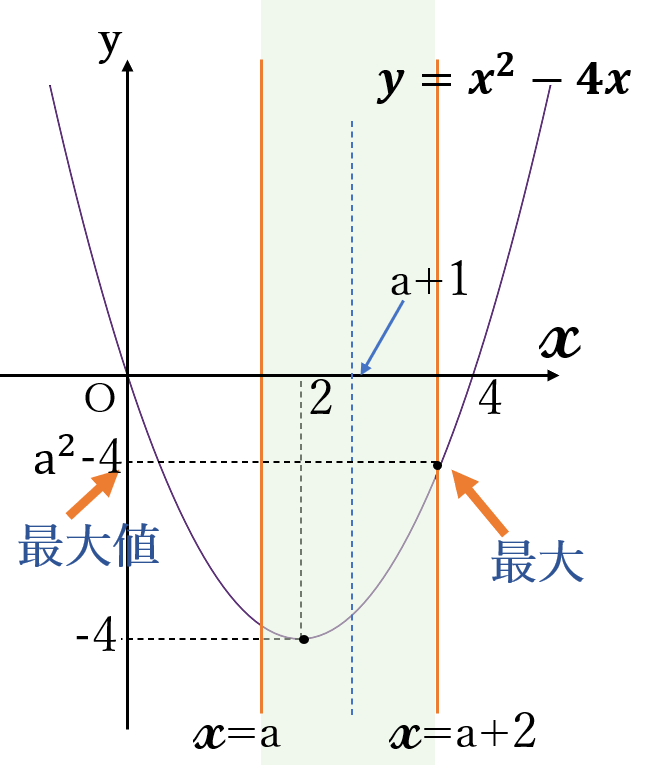
\(y=x^2-4x \ \)は、
定義域の右端
\( \ x=a+2 \ \)
で最大となります。
\(x=a+2 \ \)のとき、\(y=(a+2)^2-4(a+2)=a^2-4\)
最大値\( \ a^2-4\) \((x=a+2)\)
(ⅱ) \(a+1 ≦ 2 \ \)すなわち\( \ a ≦ 1 \ \)のとき
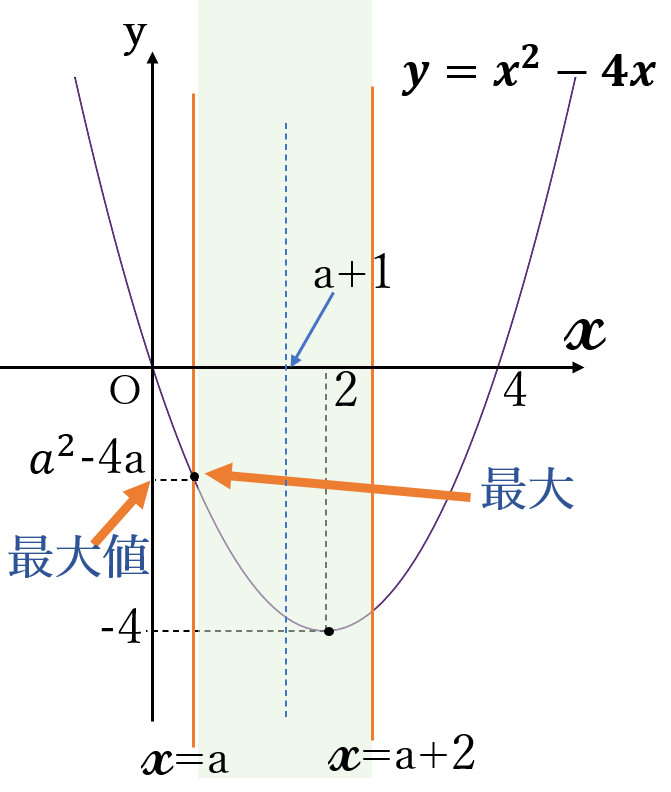
\(y=x^2-4x \ \)は、
定義域の左端
\( \ x=a \ \)
で最大となります。
\(x=a \ \)のとき、\(y=a^2-4a\)
最大値\( \ a^2-4a\) \((x=a)\)
例13 最大値を\(M(a)\)としてまとめると
\(\begin{eqnarray} M(a) = \begin{cases} a^2-4 & ( a ≧ 1 ) \\ a^2-4a & ( a ≦ 1 ) \end{cases} \end{eqnarray} \)\( \ \cdots \ \)(答)
練習8
2次関数 $$ \large y=x^2-4x+2 ( \ a≦x≦a+2 \ ) $$について、次の問いに答えよ。
(1) 最大値と、そのときの\( \ x \ \)の値を求めなさい。
(2) 最小値と、そのときの\( \ x \ \)の値を求めなさい。
解答
\(\large y=x^2-4x+2\)
\(\large =(x-2)^2-2 ( \ a≦x≦a+2 \ ) \ \cdots \ (\ast)\)
頂点\( \ (2, \ -2)\) 軸 \(x=2\)
(1)
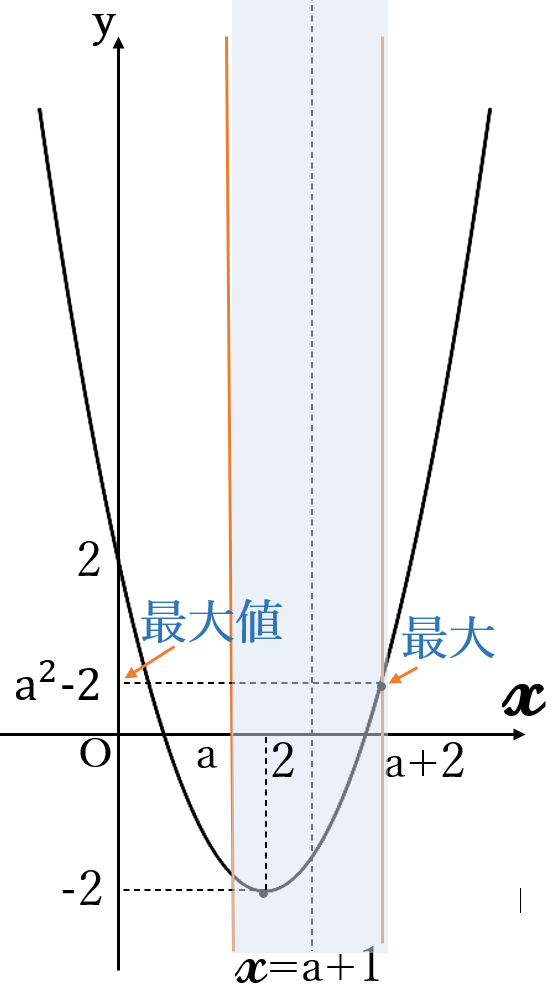
(ⅰ) \(2 \lt a+1 \ \)すなわち
\( \ a \gt 1 \ \)のとき
\(x=a+2 \ \)のとき\( \ (\ast) \ \)は
最大になり最大値は
\(y=a^2-2\)
最大値\( \ a^2-2\) \((x=a+2)\)
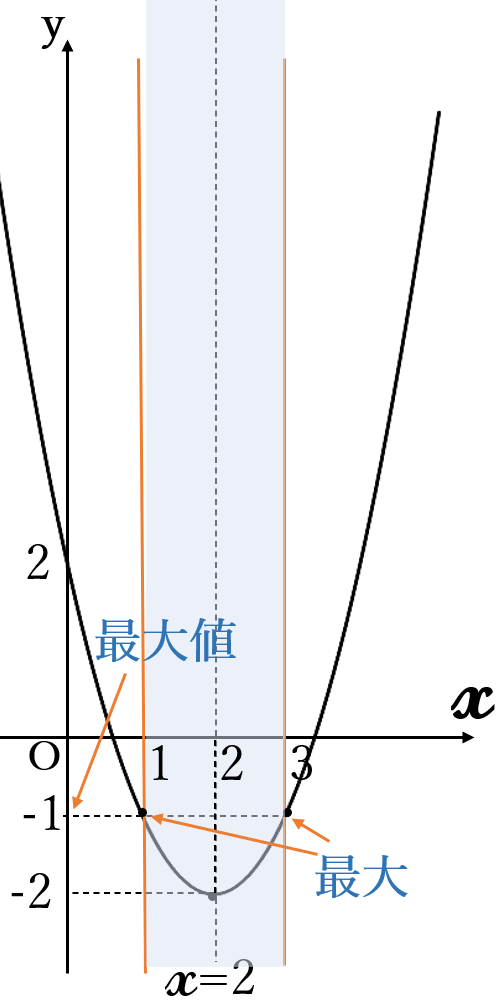
(ⅱ) \(2=a+1 \ \)
すなわち
\( \ a=1 \ \)のとき
\(x=1, \ 3 \ \)のとき\( \ (\ast) \ \)は
最大になり最大値は
\( \ y=-1\)
最大値\( \ -1\) \((x=1, \ 3)\)
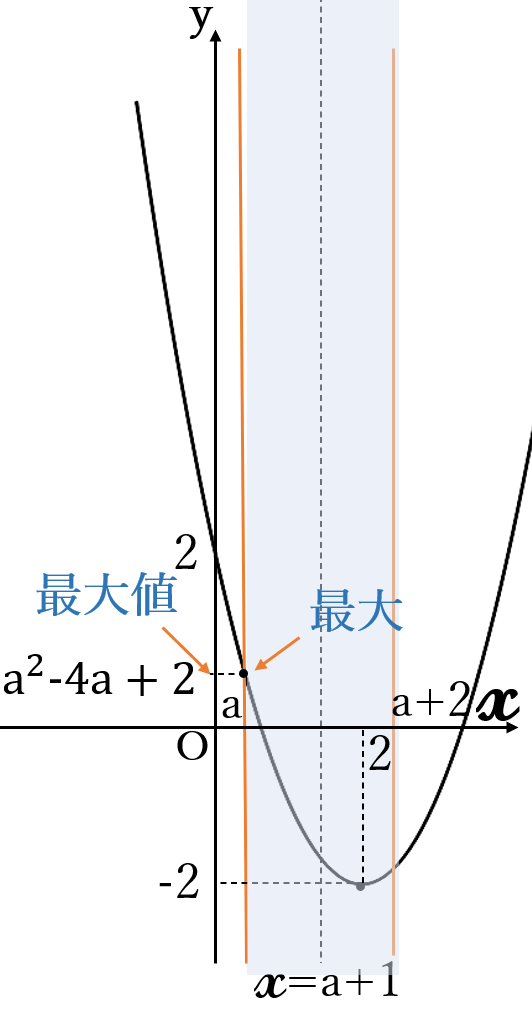
(ⅲ) \(2 \gt a+1 \ \)
すなわち
\( \ a \lt 1 \ \)のとき
\(x=a \ \)のとき\( \ (\ast) \ \)は
最大になり最大値は
\(y=a^2-4a+2\)
最大値\( \ a^2-4a+2\)
\((x=a)\)
練習8(1)
最大値を\(M(a) \ \)としてまとめると
\(\begin{eqnarray} M(a)= \begin{cases} a^2-2 & ( a ≧ 1 ) \\ a^2-4a+2 & ( a ≦ 1 ) \end{cases} \end{eqnarray} \)
\( \ \cdots \ \)(答)
解答
\(\large y=x^2-4x+2\)
\(\large =(x-2)^2-2 ( \ a≦x≦a+2 \ ) \ \cdots \ (\ast)\)
頂点\( \ (2, \ -2)\) 軸 \(x=2\)
(2)
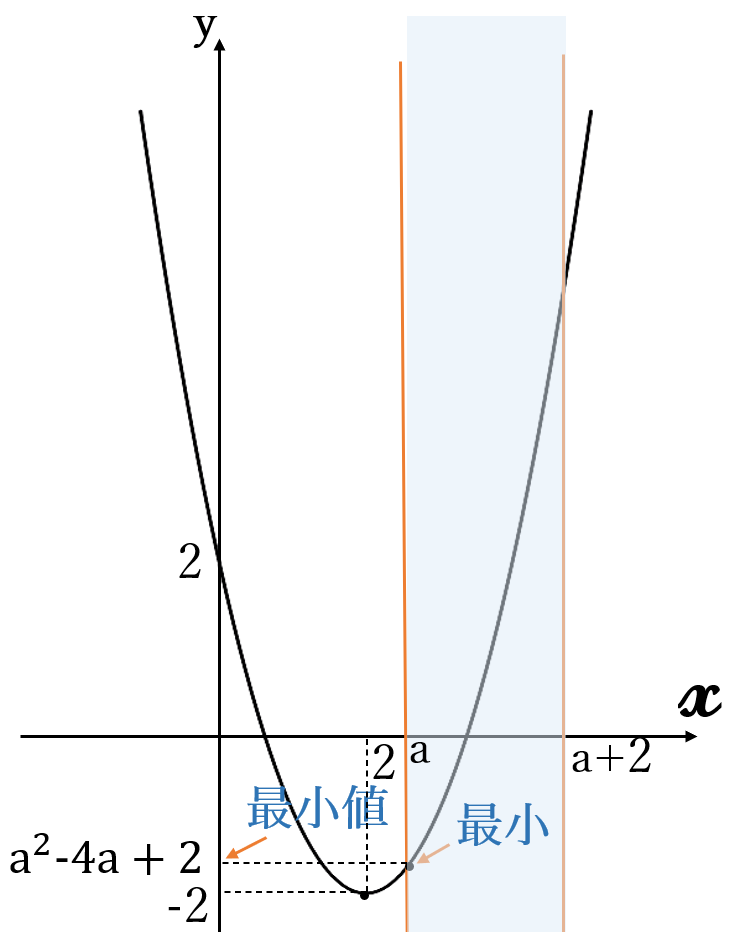
(ⅰ)\(2 \lt a \ \)のとき
最小値は
\(x=a\)
のときで最小値
\(y=a^2-4a+2\)
最小値\( \ a^2-4a+2\)
\((x=a)\)
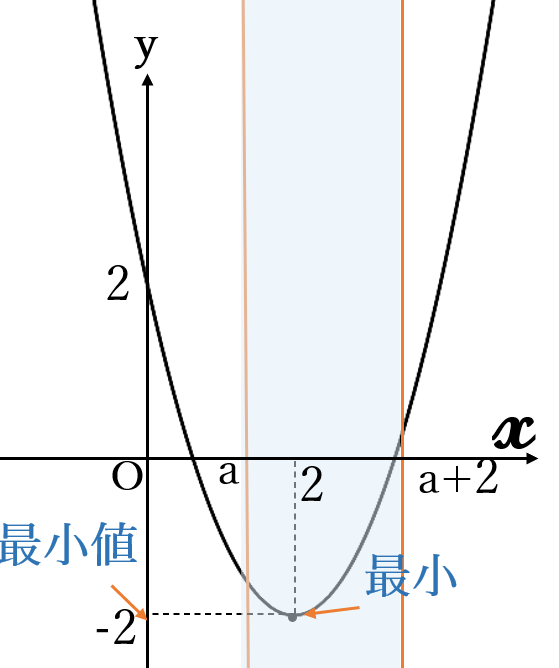
(ⅱ)\(a≦2≦a+2\)
のときすなわち
\(0≦a≦2\)
のとき最小値
\(y=2\)
最小値\( \ 2\) \((x=2)\)
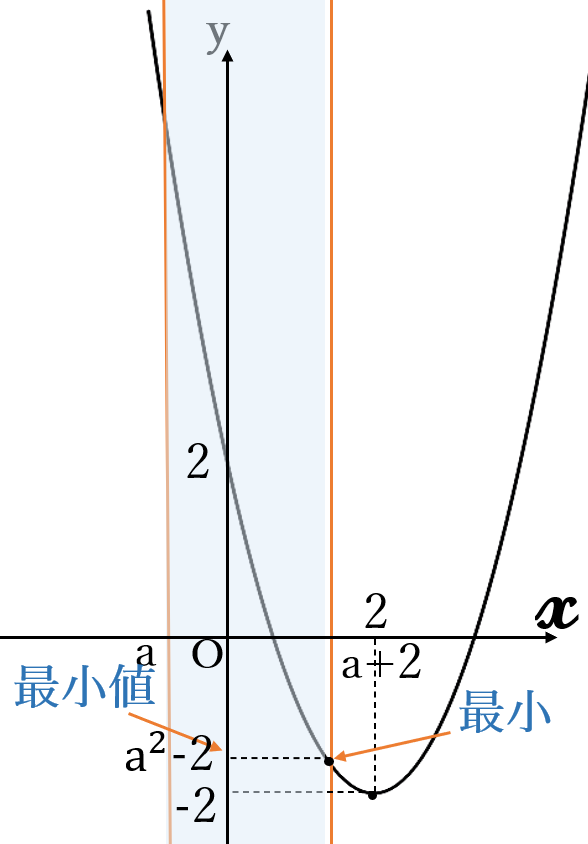
(ⅲ)\(a+2 \lt 2\)
のときすなわち
\(a \lt 0\)
のとき最小値
\(y=\{(a+2)-2\}^2\)
\(-2\)
\(=a^2-2\)
最小値\( \ a^2-2\)
\((x=a+2)\)
練習8(2) 最小値を\(m(a)\)としてまとめると
\(\begin{eqnarray} m(a) = \begin{cases} a^2-2 & ( a \lt 0 ) \\ 2 & ( 0 ≦ a ≦ 2 ) \\ a^2-4a+2 & ( a \gt 2 ) \end{cases} \end{eqnarray}\)
\( \ \cdots \ \)(答)
