2次関数の増加減少と
最大値最小値 その2
定義域に制限があるとき
関数の増加減少、放物線の頂点の座標、定義域
の3つを総合的にみて2次関数の最大値最小値を求める必要があります。そのため、下の二つのパターンに分けて答えを求めることになります。
(ⅰ) 頂点の\(x\)座標が定義域の内側にある場合
(ⅱ) 頂点の\(x\)座標が定義域の外側にある場合
(ⅰ) 頂点の\(x\)座標が定義域の内側にある場合
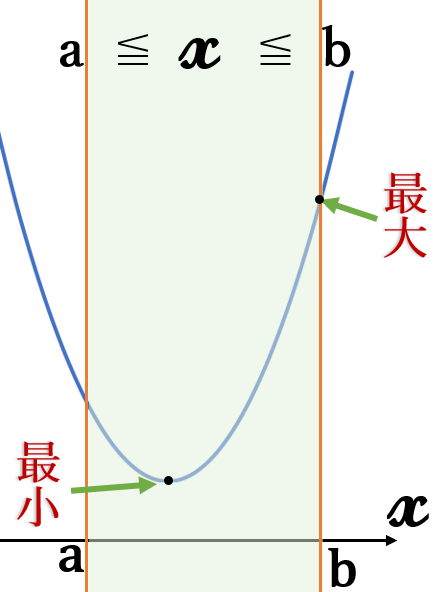
下に凸の場合、頂点の
\( \ y \ \)座標が最小値になります。
最大値は、定義域の端点の
\( \ y \ \)座標が大きい方です。
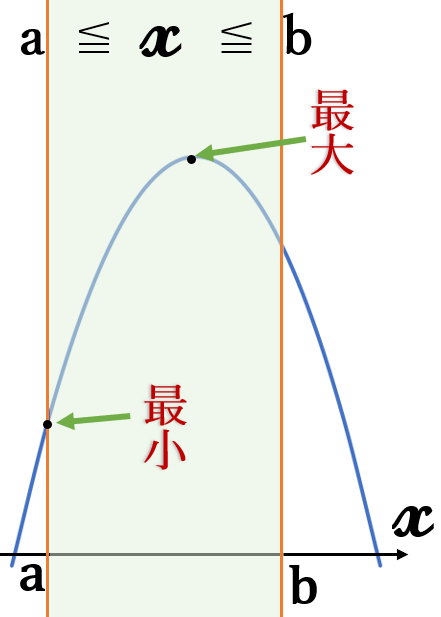
上に凸の場合、頂点の
\( \ y \ \)座標が最大値になります。
最小値は、定義域の端点の
\( \ y \ \)座標が小さい方です。
(ⅱ) 頂点の\(x\)座標が定義域の外側にある場合
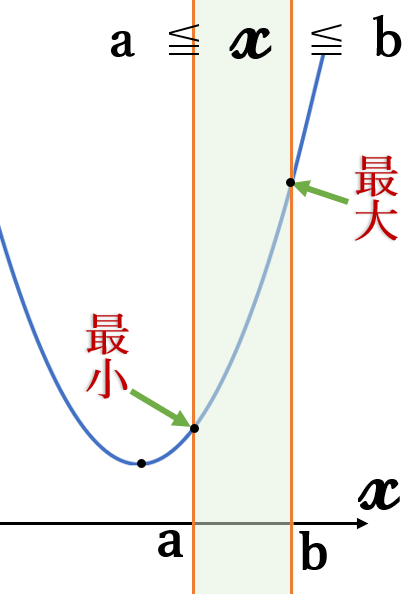
定義域の端点の
\( \ y \ \)座標の
大きい方が最大値、
小さい方が最小値
になります。
例や例題をよく読んで、練習問題を解くことで理解しましょう。
例6
\(y=(x-3)^2-1\) \(( \ 0 \ \)≦\( \ x \ \)≦\( \ 5 \ )\)
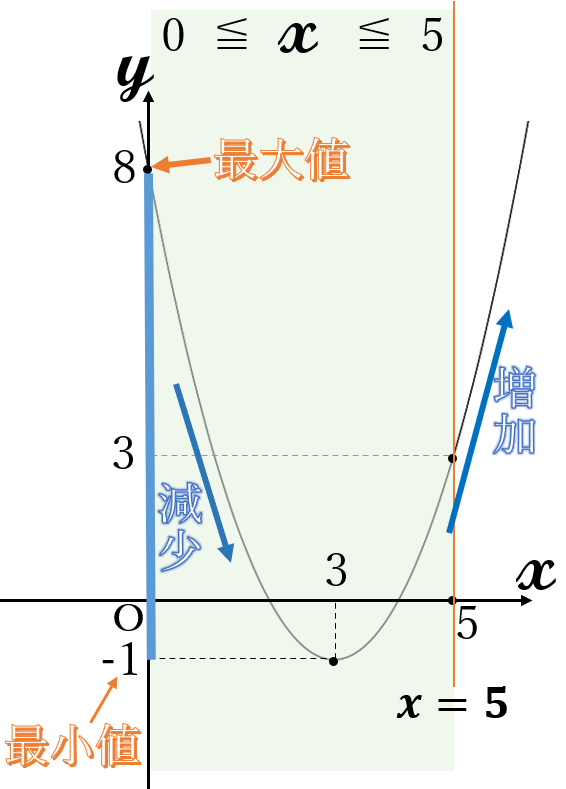
頂点\( \ (3, \ -1) \ \)
下に凸
最大値 \(8\) \((x=8)\)
最小値 \(-1\) \((x=3)\)
定義域内のグラフで、一番上にある点の\( \ y \ \)座標が最大値、一番下にある点の\( \ y \ \)座標が最小値です。
この2次関数は、下に凸の放物線で頂点が定義域の内側にあるので、頂点の\( \ y \ \)座標が最小値になります。
例7
\(y=(x-3)^2-1\) \(( \ 0 \ \)≦\( \ x \ \)≦\( \ 2 \ )\)
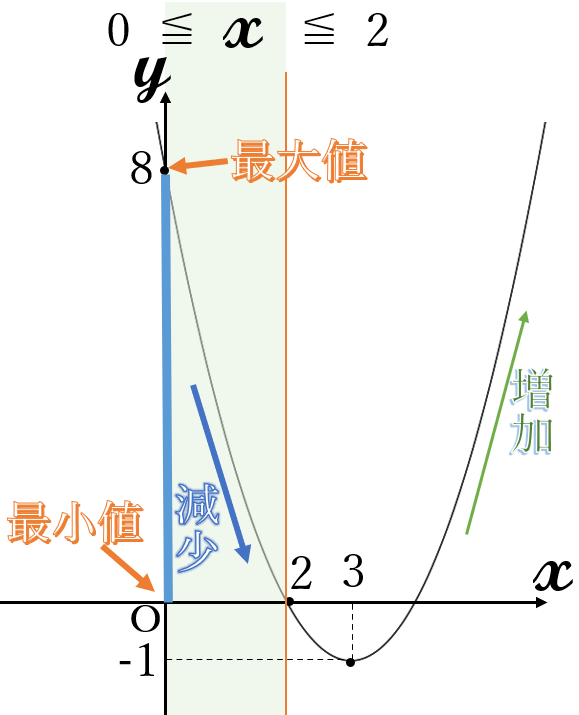
頂点\( \ (3, \ -1) \ \)
下に凸
最大値 \(8\) \((x=8)\)
最小値 \(0\) \((x=2)\)
定義域内のグラフで、一番上にある点の\( \ y \ \)座標が最大値、一番下にある点の\( \ y \ \)座標が最小値です。
この2次関数は、下に凸の放物線で頂点が定義域の外側にあるので、端点の\( \ y \ \)座標が最大値最小値になります。
例8
\(y=-(x-1)^2+7\) \(( \ -1 \ \)≦\( \ x \ \)≦\( \ 4 \ )\)
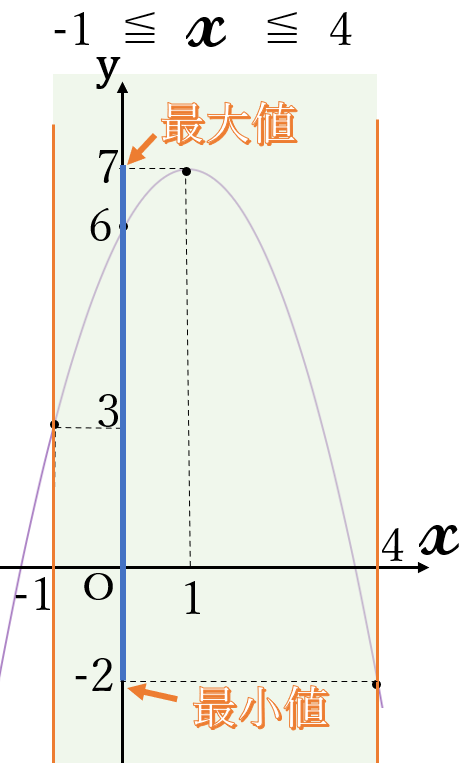
頂点\( \ (1, \ 7) \ \)
上に凸
最大値 \(7\) \((x=1)\)
最小値 \(-2\) \((x=4)\)
定義域内のグラフで、一番上にある点の\( \ y \ \)座標が最大値、一番下にある点の\( \ y \ \)座標が最小値です。
この2次関数は、上に凸の放物線で頂点が定義域の内側にあるので、頂点の\( \ y \ \)座標が最大値になります。
例9
\(y=-(x-1)^2+7\) \(( \ 2 \ \)≦\( \ x \ \)≦\( \ 4 \ )\)
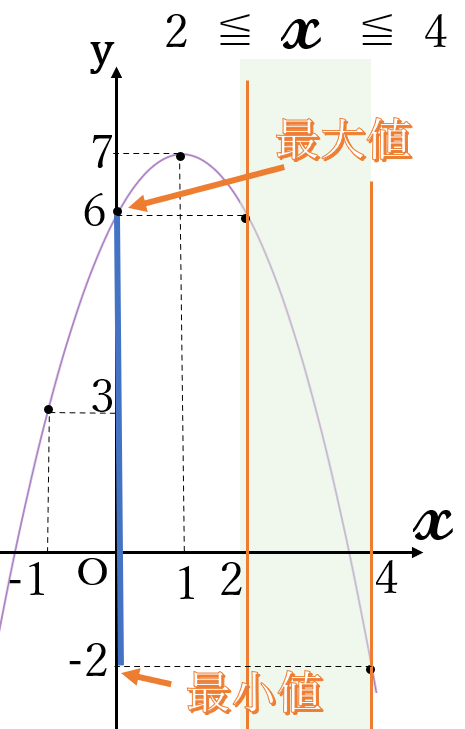
頂点\( \ (3, \ -1) \ \)
上に凸
最大値 \(6\) \((x=2)\)
最小値 \(-2\) \((x=4)\)
定義域内のグラフで、一番上にある点の\( \ y \ \)座標が最大値、一番下にある点の\( \ y \ \)座標が最小値です。
この2次関数は、上に凸の放物線で頂点が定義域の外側にあるので、端点の\( \ y \ \)座標が最大値最小値になります。
例題5
次の関数に最大値、最小値があれば、それを求めなさい。
(1) \(\large y=x^2-2x-3\) \((-2 \ \)≦\( \ x \ \)≦\( \ 2 \ )\)
(2) \(\large y=-2x^2-12x-8\) \((-2 \ \)≦\( \ x \ \)≦\( \ 0 \ )\)
(3) \(\large y=-x^2+4x\) \(( \ 1 \ \lt x \lt \ 5 \ )\)
解答
(1) \(y=x^2-2x-3\) \(( \ -2 \ \)≦\( \ x \ \)≦\( \ 2 \ )\)
\(\large y=x^2-2x-3=(x-1)^2-4\)
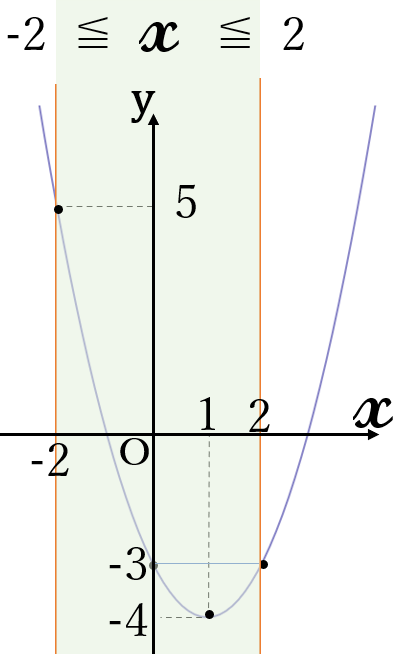
頂点\( \ (1, \ -4)\)
下に凸
頂点が定義域の範囲内にあります。したがって、頂点の\( \ y \ \)座標が最小値になります。
最大値は、定義域の端点の\( \ y \ \)座標の大きい方です。したがって、\(x=-2 \ \)のとき
\(y=(-2-1)^2-4\)
\(=(-3)^2-4=9-4=5\)
\(x=2 \ \)のとき
\(y=(2-1)^2-4=1^2-4=-3\)
以上より
最大値 \(5\) \((x=-2)\)
最小値 \(-4\) \((x=1)\)
解答
(2) \(y=-2x^2-12x-8\) \(( \ -2 \ \)≦\( \ x \ \)≦\( \ 0 \ )\)
\(\large y=-2x^2-12x-8=-2(x+3)^2+10\)
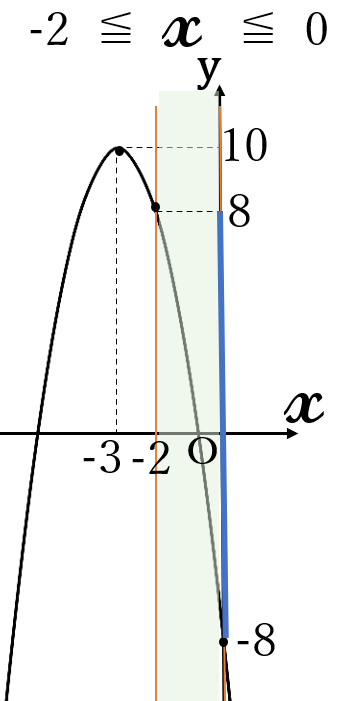
頂点\( \ (-3, \ 10)\) 上に凸
頂点が定義域の外にあります。したがって、最大値は、定義域の端点の\( \ y \ \)座標の大きい方、最小値は、定義域の端点の\( \ y \ \)座標の小さい方です。
よって、\(x=-2 \ \)のとき
\(y=-2\times (-2+3)^2+10\)
\(=-2\times 1+10=8\)
\(x=0 \ \)のとき
\(y=-2\times (0+3)^2+10\)
\(=-2\times 9+10=-8\)
以上より
最大値 \(8\) \((x=-2)\)
最小値 \(-8\) \((x=0)\)
注意
\(a \ \)≦\( \ x \ \)≦\( \ b\) を、閉区間
\(a \lt x \lt b\) を、開区間といいます。
最大値最小値の問題では、定義域は、
閉区間(\(a \ \)≦\( \ x \ \)≦\( \ b\))で与えられることが一般的です。
しかし、ときどき例題5(3)のように開区間(\(a \lt x \lt b\))で与えられることがあります(教科書・参考書によります)。
定義域が開区間で与えられたときの解答については、次の例題5(3)の解答を参考にしてください。
解答
(3) \(y=-x^2+4x\) \(( \ 1 \ \lt x \lt \ 5 \ )\)
\(\large y=-x^2+4x=-(x-2)^2+4\)
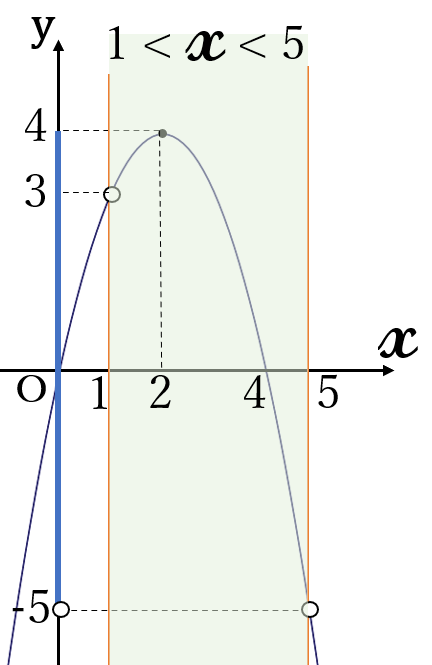
頂点\( \ (2, \ 4)\) 上に凸
頂点が定義域の内側にあります。したがって、最大値は、頂点の\( \ y \ \)座標です。
定義域が閉区間ならば最小値は、定義域の端点の\( \ y \ \)座標の小さい方になりますが、開区間なので最小値はありません。以上より
最大値 \(4\) \((x=2)\)
最小値はない
\(x \ \)が限りなく5に近づくとき、\(y \ \)の値は限りなく\( \ -5 \ \)に近づきますが、関数の値は定まりません。したがって、「最小値はない」となります。
練習5
次の関数に最大値、最小値があれば、それを求めなさい。
(1) \(\large y=x^2-2x+2\) \( \ (0 \ \)≦\( \ x \ \)≦\( \ 3 \ )\)
(2) \(\large y=-x^2+1\) \( \ (1\ \)≦\( \ x \ \)≦\( \ 3 \ )\)
解答
(1) \(\large y=x^2-2x+2\) \( \ (0 \ \)≦\( \ x \ \)≦\( \ 3 \ )\)
\(\large y=x^2-2x+2\)
\(\large =(x-1)^2+1\) \( \ (0 \ \)≦\( \ x \ \)≦\( \ 3 \ )\)
グラフは右下
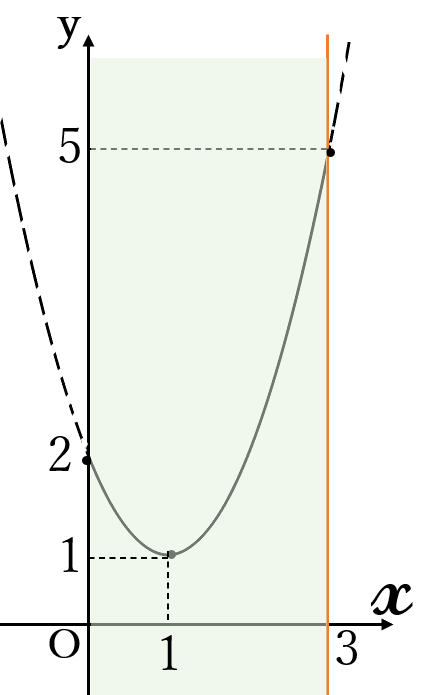
頂点\( \ (1, \ 1) \ \)
頂点が定義域内にあり、
下に凸なので
最小値 \(1\) \((x=1)\)
\(x=0 \ \)のとき、\(y=2\)
\(x=3 \ \)のとき、\(y=5\)
ゆえに
最大値 \(5\) \((x=3)\)
以上より
最大値 \(5\) \((x=3)\)
最小値 \(1\) \((x=1)\)
解答
(2) \(\large y=-x^2+1\) \( \ (1\ \)≦\( \ x \ \)≦\( \ 3 \ )\)
\(\large y=-(x-0)^2+1\) \( \ (1\ \)≦\( \ x \ \)≦\( \ 3 \ )\)
グラフは右下
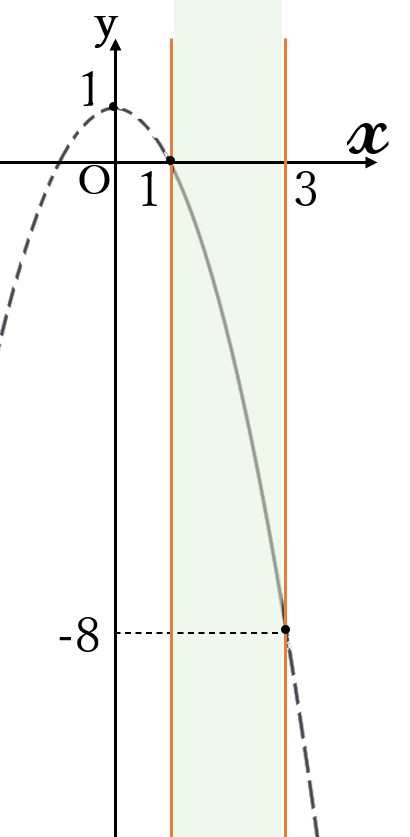
頂点\( \ (0, \ 1) \ \)
頂点が定義域外にあるので、
最大値最小値は、定義域の端点の\(y \ \)座標です。
\(x=1 \ \)のとき、\(y=0\)
\(x=3 \ \)のとき、\(y=-8\)
以上より
最大値 \(0\) \((x=1)\)
最小値 \(-8\) \((x=3)\)
