三角形の外角(外角定理)
基本中の基本です。頻繁(ひんぱん)に使います。
問題1
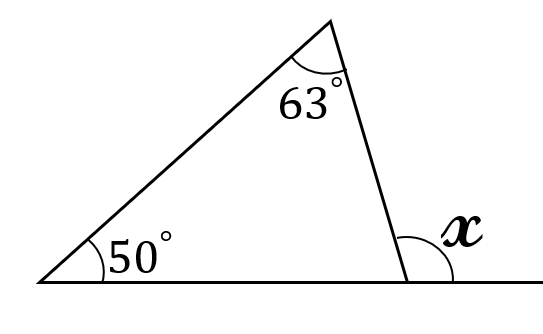
右の図において、
\(\angle x \ \)の大きさを
求めなさい。
解答
(答) \(\Large 113^{\circ}\)
\(x=50^{\circ}+63^{\circ}\)
\(=113^{\circ}\)
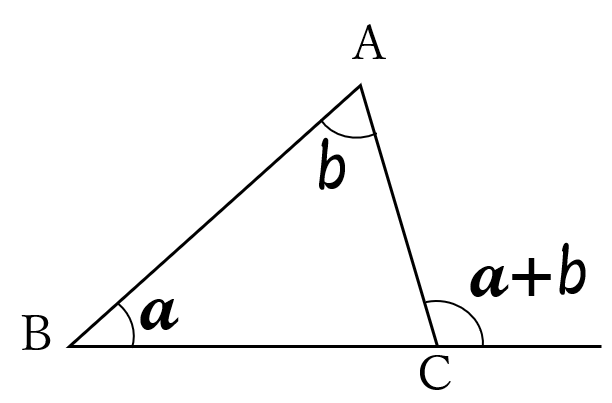
《外角定理》
三角形の外角は、それと隣り合わない二つの内角の和に等しい。
右上図で暗記しておきましょう。
証明は以下の
通りです。
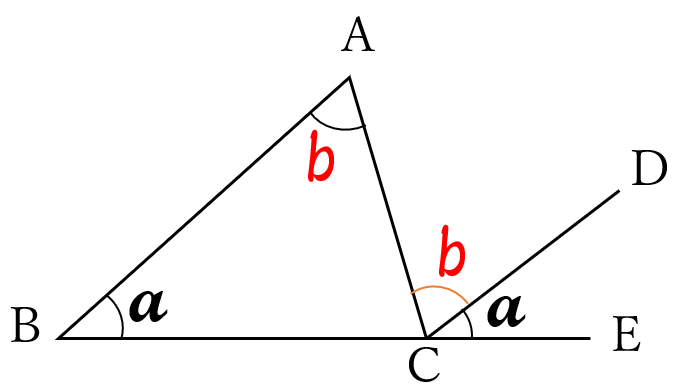
\(AB//DC \iff \angle ABC =\angle DCE \ \)(同位角)
\(\angle BAC =\angle ACD \ \)(錯角)
よって、\(\angle ACE =\angle DCE + \angle ACD\)
\(=\angle ABC + \angle BAC=a+b\)
前問の確認です。
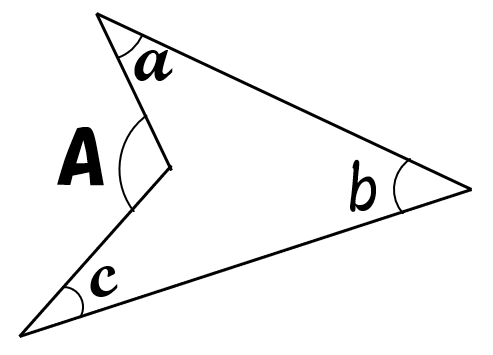
問題6
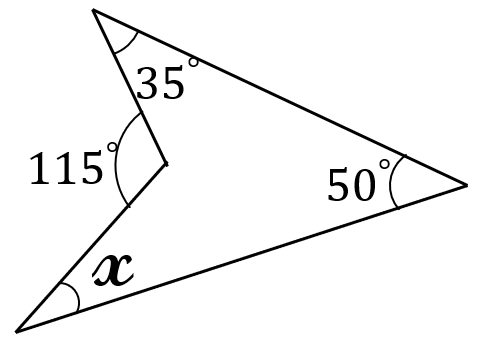
右の図の\(\angle x \ \)の
大きさを求めなさい。
解答
(答) \(\Large 30^{\circ}\)
このような図形
では、
右上図⇒と一緒に
\(A=a+b+c\)
と覚えておけば、
\(x+35^{\circ}+50^{\circ}=115^{\circ}\)
から
\(x=115^{\circ}-35^{\circ}-50^{\circ}=30^{\circ}\)
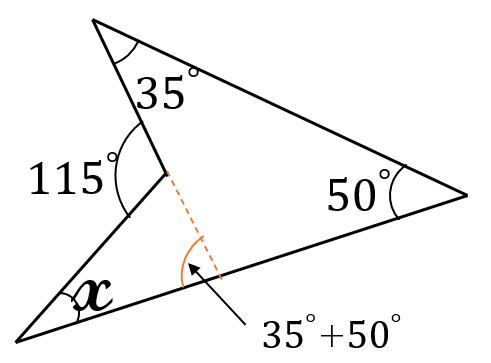
右下の図のように⇒
補助線を引いて
考えても良いです。
前問の確認です。
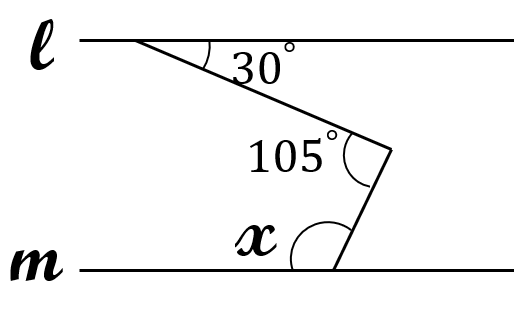
問題3
下の図において、\(l//m \ \)です。
\(\angle \ x \ \)の大きさを求めなさい。
解答
(答) \(\Large 105^{\circ}\)
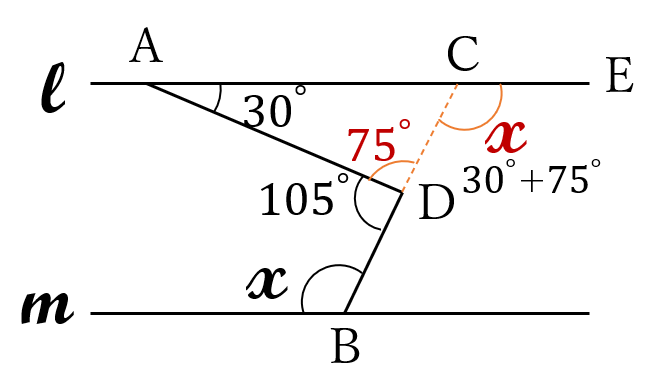
補助線の引き方はいくつかありますが、下の図のように補助線を引くと、
\(\angle ADC = 180^{\circ}-105^{\circ}=75^{\circ}\)
\(x=\angle ECB \ \)(錯角)
よって、\(x=\angle ECB =30^{\circ}+ 75^{\circ}=105^{\circ}\)
問題13
下の図において、\(\angle \ \)\(\Large x \ \)の大きさを求めなさい。
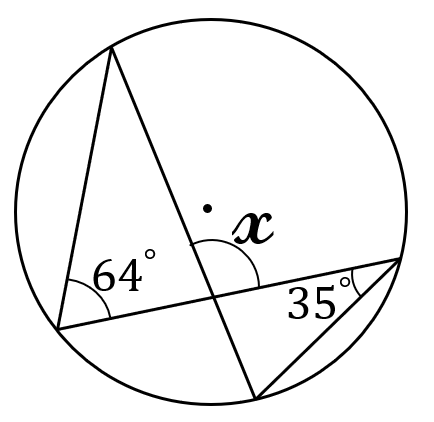
解答
(答) \(\Large 99^{\circ}\)
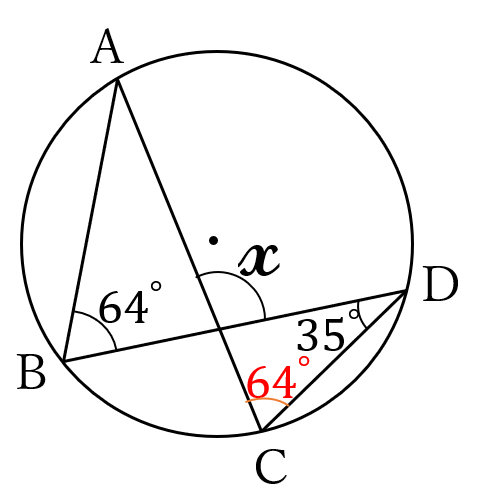
同じ弧に対する円周角は等しいので
\(\angle ACD = \angle ABD =64^{\circ}\)
よって、\(\large x\)\(=64^{\circ}+35^{\circ}\)\(\large =99^{\circ}\)
問題14
下の図において、円周上に4点\( \ A, \ B, \ C, \ D\)
があります。線分\(AC \ \)は直径です。
\(\angle \ \)\(\large x \ \)の大きさを求めなさい。
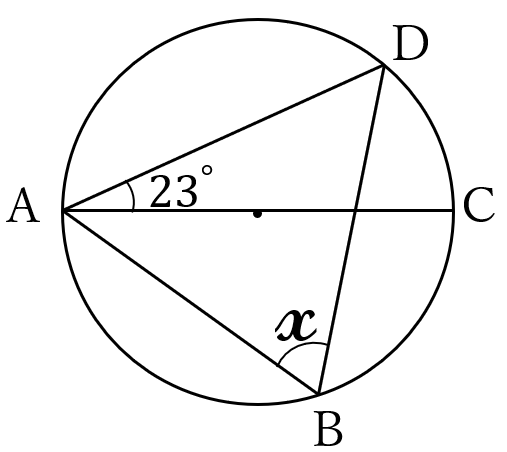
解答
(答) \(\Large 67^{\circ}\)
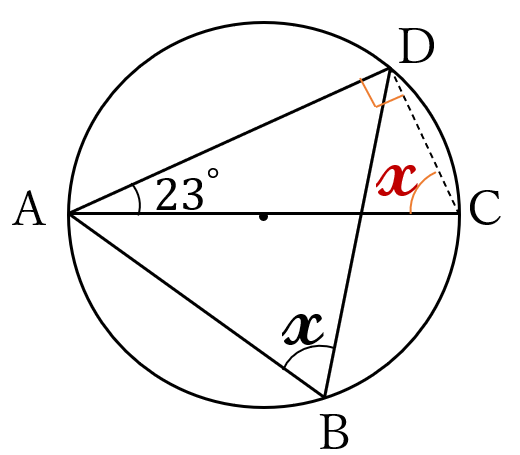
点\(D \ \)と点\(C \ \)を
結びます。
直径に対する円周角より、\(\angle ADC =90^{\circ} \ \)
よって、
\(\angle ACD = 90^{\circ}-23^{\circ}=67^{\circ}\)
弧\(AD \ \)に対する円周角より
\(\large x \)\((\angle ABD)=\angle ACD\)\(\large =67^{\circ}\)
問題 23
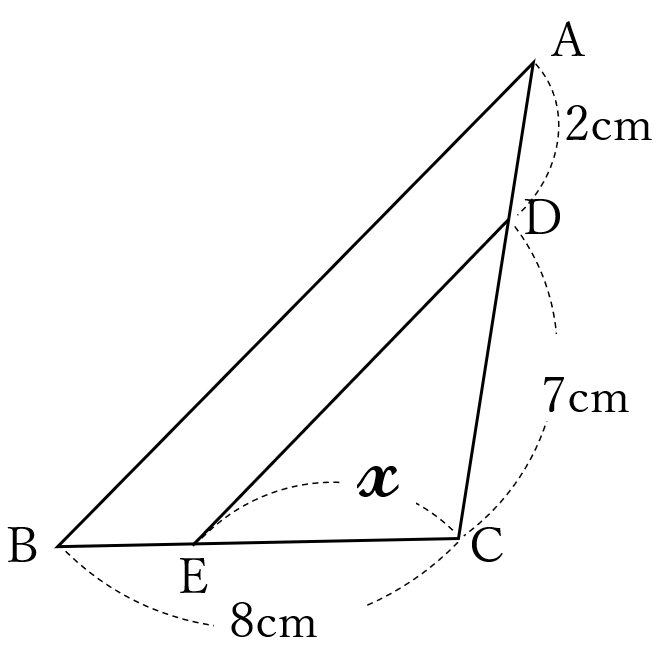
右図の\(\triangle ABC\)
において、
点\(D \ \)は辺\(AC \ \)上の、
点\(E \ \)は辺\(BC \ \)上の
点で、
\(AB//DE \ \)です。
\(AD=2cm\)
\(DC=7cm\)
\(BC=8cm\)
のとき、線分\(EC \ \)の長さ\(x \ \)を求めなさい。
解答
(答) \(\Large \frac{56}{9}\) \((cm)\)
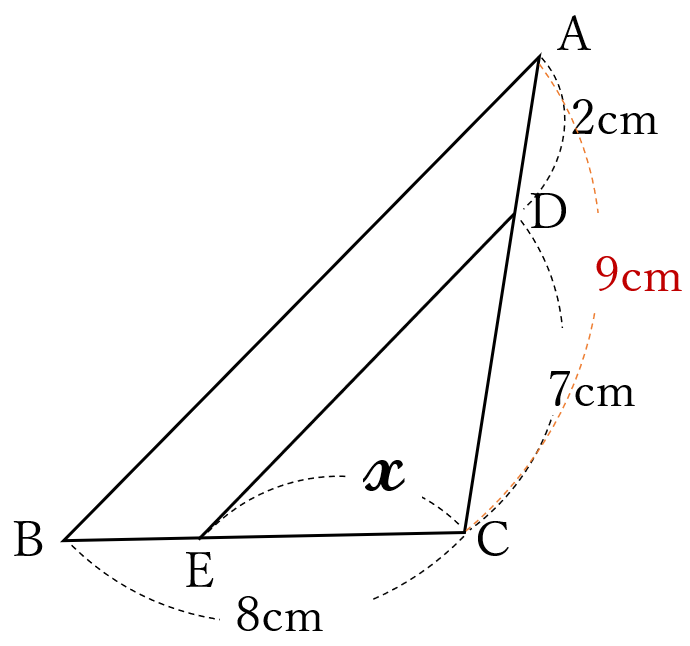
\(AB//DE \ \)より、
\(\triangle ABC \ \)∽\( \ \triangle DEC\)
\(AC=9 \ cm \ \)より、
\(AC:DC=9:7\)
だから
\(\triangle ABC \ \)と\( \ \triangle DEC \ \)の
相似比は \(9:7\)
よって、
\(DC \ \)は\(AC \ \)の\(\frac{7}{9} \ \)倍です。
\(EC \ \)も\(BC \ \)の\(\frac{7}{9} \ \)倍です。
したがって、\(x \ (EC)=BC\times \frac{7}{9}=8\times \frac{7}{9}=\frac{56}{9}\)
\(8:x=9:7 \ \)から計算しても良いですが、暗算だとちょっと厳しかもしれません。
問題21
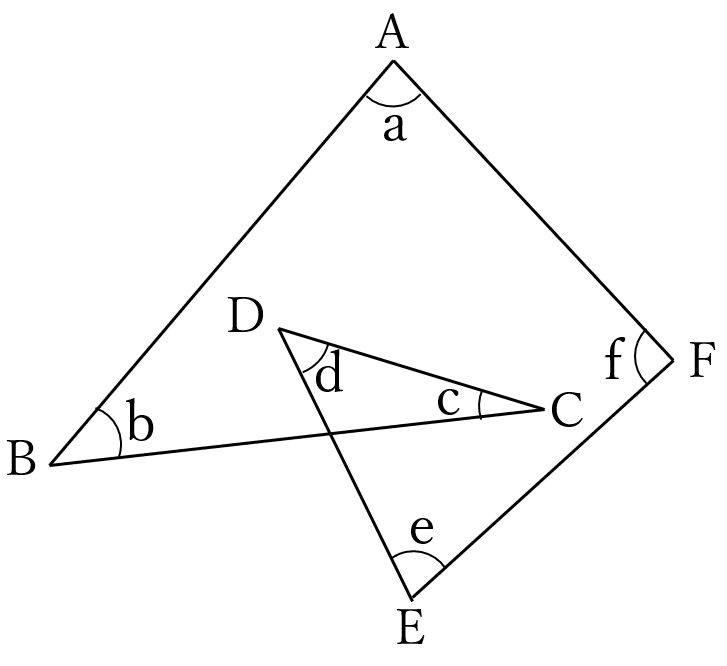
下の図で、
\(\angle A =a, \ \angle B =b, \ \angle C =c\)
\(\angle D =d, \ \angle E =e, \ \angle F =f\)
とします。
\(a+b+c+d+e+f\) を求めてください。
解答
(答) \(\Large 360^{\circ}\)
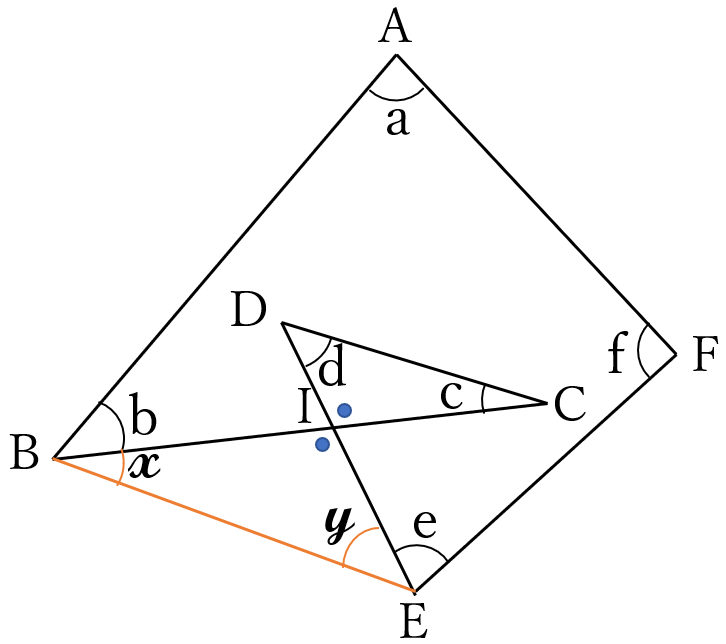
右の図で、点\(B \ \)と点\( \ E \ \)を結び、線分\(CB \ \)と線分\(DE \ \)の交点を\(I \ \)とします。
\(\angle IBE =x, \ \angle IEB =y \ \)とおくと
\(\angle DIC = \angle EIB\) (対頂角)ゆえ
\(c+d=x+y\) よって、
\(a+b+c+d+e+f=a+b+x+y+e+f\)
これは、四角形\(ABEF\)の内角の和です。したがって、
\(a+b+c+d+e+f=360^{\circ}\)
問題52
下の図のように、ある円の円周上に7点 $$ A, \ B, \ C, \ D, \ E, \ F, \ G $$ があります。その7点を $$ A \rightarrow C \rightarrow E \rightarrow G \rightarrow B \rightarrow D \rightarrow F \rightarrow A $$ の順に結んだときにできる角
\(a,b,c,d,e,f,g \ \)の和を求めてください。
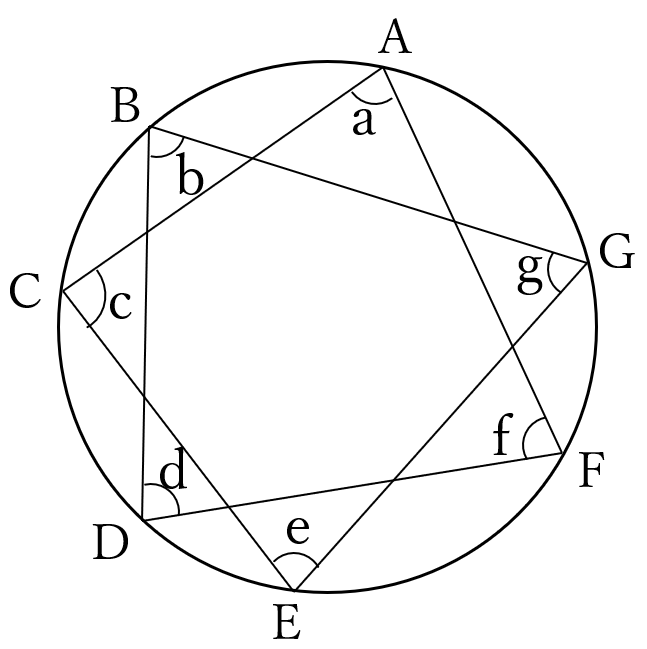
解答
(答) \(\Large 540^{\circ}\)
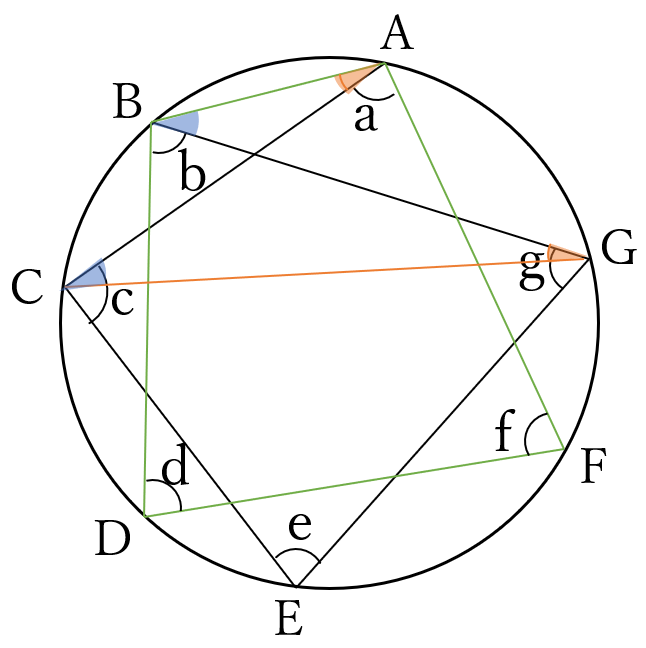
点\( \ A \ \)と\( \ \ B \ \)、点\( \ C \ \)と\( \ \ G \ \)を結びます。
\(\angle ACG =\angle ABG, \ \angle BGC = \angle BAC \ \)だから、
\(a+b+c+d+e+f+g \ \)は、
四角形\(ABDF\)の内角と\(\triangle GCE\)の内角の和に等しい。
よって、\(a+b+c+d+e+f+g=360^{\circ}+180^{\circ}=540^{\circ}\)
別解
この問題では、円周上の7つの点は不規則に並んでいるものとしていますが、等間隔に並んでいても答えは同じになるはずです。したがって、等間隔に並んでいるものとして解答します。
円周上の7点が等間隔に並んでいると仮定します。
\(a=b=c=d=e=f=g=x \ \)とおくと
\(a+b+c+d+e+f+g=7x\)
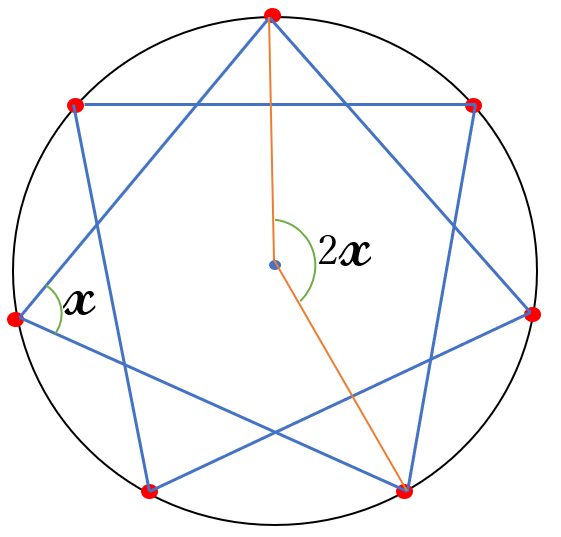
右図より
\(2x=\)\(\large \frac{3}{7}\)\( \times 360^{\circ}\)
\(x=\)\(\large \frac{3}{7}\)\( \times 180^{\circ}\)
\(7x=3 \times 180^{\circ}\)
\( \ =\)\(\Large 540^{\circ}\)
この解答だと、暗算ではちょっと苦しいです。
参考
この問題の類題が、令和3年(2021年)兵庫県高校入試に出題されてます。ただし、こちらはもっと発展した難問になってました。
抜粋すると、次のような問いになってます。
(3) 円周を\( \ n \ \)等分する点を、2つ目ごとに結んでできる星形正\( \ n \ \)角形の先端部分の\( \ n \ \)個の角の和は何度か、\( \ n \ \)を用いて表しなさい。ただし、\( \ n \ \)は5以上の整数で、星形正\( \ n \ \)角形がかけない\( \ n \ \)は除くものとする。
(答) 別解の計算方法で解けます。
\( \ n \ \)は5以上の奇数です。
\(2x=\)\(\large \frac{n-4}{n}\)\( \times 360^{\circ} \ ,\) \(x=\)\(\large \frac{n-4}{n}\)\( \times 180^{\circ}\)
\(nx=\)\(\Large (n-4) \times 180^{\circ}\) ・・・(答)
問題7の星形5角形のように、各頂点が円周上になくても、星形\( \ n \ \)角形の角の和は、\((n-4)\times 180^{\circ} \ \)になります。ただし、\( \ n \ \)は奇数です。詳細は次ページ⇒
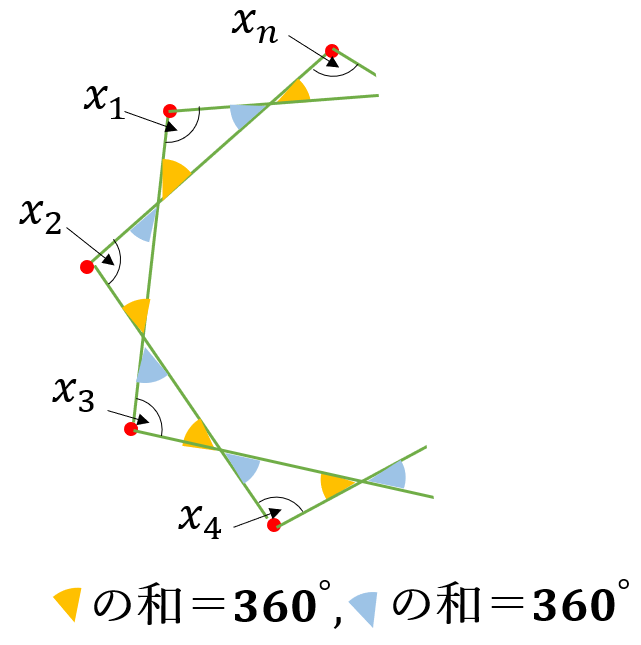
右の図のような、星形\( \ n \ \)角形は、内側に\( \ n \ \)角形があり、各辺に三角形が\( \ n \ \)個乗っている形になってます。\(n \ \)個の三角形の内角の総和は
\(180^{\circ} \times n \ \cdots \ \)①
内側の\( \ n \ \)角形の外角の和は\( \ 360^{\circ} \ \)
外角は、2種類あるので\( \ 360^{\circ} \times 2 \ \cdots \ \)②
①②より
\(x_{1}+x_{2}+x_{3}+ \cdot \cdot \cdot +x_{n} +360^{\circ} \times 2\)
\(=180^{\circ}\times n\)
\(x_{1}+x_{2}+x_{3}+ \cdot \cdot \cdot +x_{n}\)
\(=180^{\circ}\times n-180^{\circ} \times 4 =180^{\circ}\times (n-4)\)
\(\Large =(n-4)\times 180^{\circ}\)
星形5角形の角の和は
\((5-4)\times 180^{\circ}=180^{\circ}\)
星形7角形の角の和は
\((7-4)\times 180^{\circ}=540^{\circ}\)
星形9角形の角の和は
\((9-4)\times 180^{\circ}=900^{\circ}\)
です。
この兵庫県の入試問題では続きがあって、(4)として次の問題が出題されてました。かなりの難問で、限られた時間で解くことは困難かと思われます。
(4) 円周を24等分する点をとった場合、星形24角形は何種類かくことができるか、求めなさい。また、それらの先端部分の1個の角について、その大きさが最も小さいものは何度か、求めなさい。ただし、同じ形の図形は1種類として数えることとする。
解答例
24等分する点を\( \ k \ \)個目ごとに結んで星形正24角形が作れるのは、\( \ k \ \)と\( \ 24 \ \)が互いに素のときです。ただし、\(2 ≦ k ≦ 12 \ \)です。\(k ≧ 13 \ \)は逆回りで同じことになります。\(k=1 \ \)は星形にならないので除外します。
\(k \ \)と24が互いに素ならば、\(k \ \)と24の最小公倍数が\( \ k \times 24 \ \)となり、すべての点を直線で結んでからスタートの点に戻り、星形正24角形が作れます。
互いに素とは❓
【2つの整数 \(a\) と \(b\) が互いに素】
\(a\) と \(b\) の公約数が1のみのとき(1以外に公約数がないとき)、
「\( \ a \ \)と\( \ b \ \)は互いに素」といいます。
\(k=2,3,4,6,8,12\) は、24の約数なので、1週目でスタートの点に戻ってしまい、24角形は描けません。
候補は、
\(k=5,7,9,10,11\)
です。
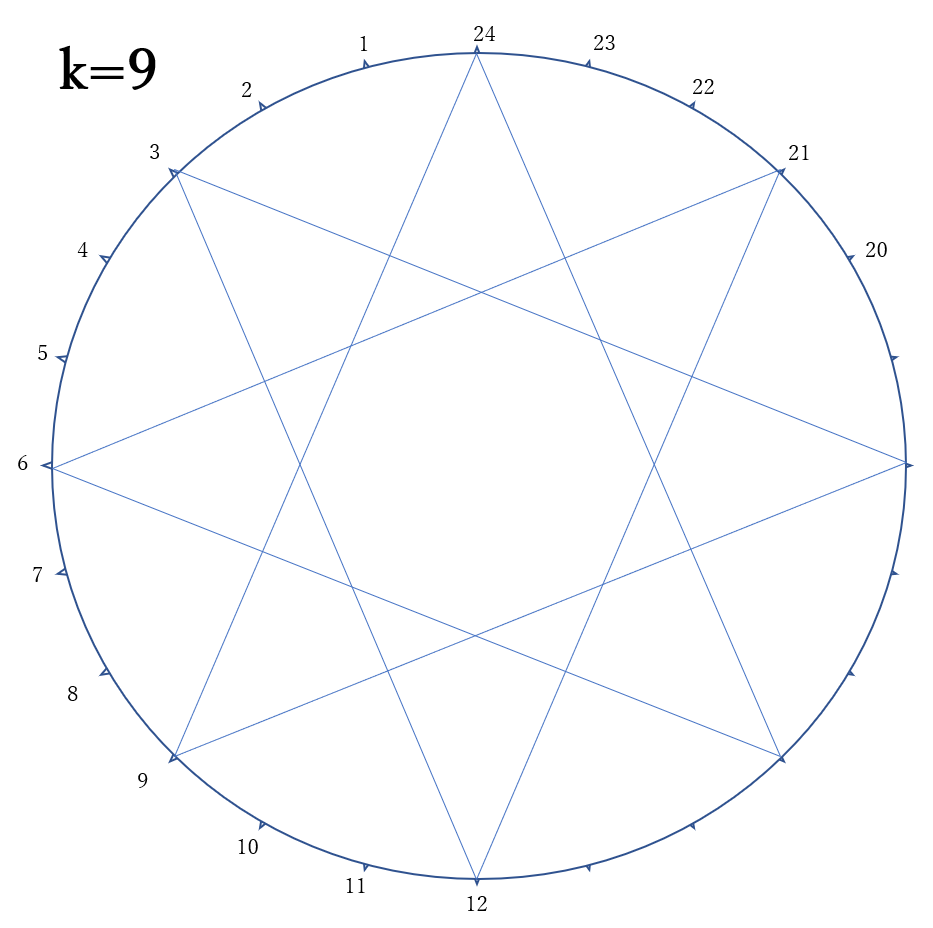
《\(k=9 \ \)のとき》
9と24は互いに素ではありません。9と24の最小公倍数は\( \ 9 \times 8=72 \ \)ですら、8本目の直線を引いたときにスタートの点に戻ってしまい、星形正8角形になってしまいます。
右上の図
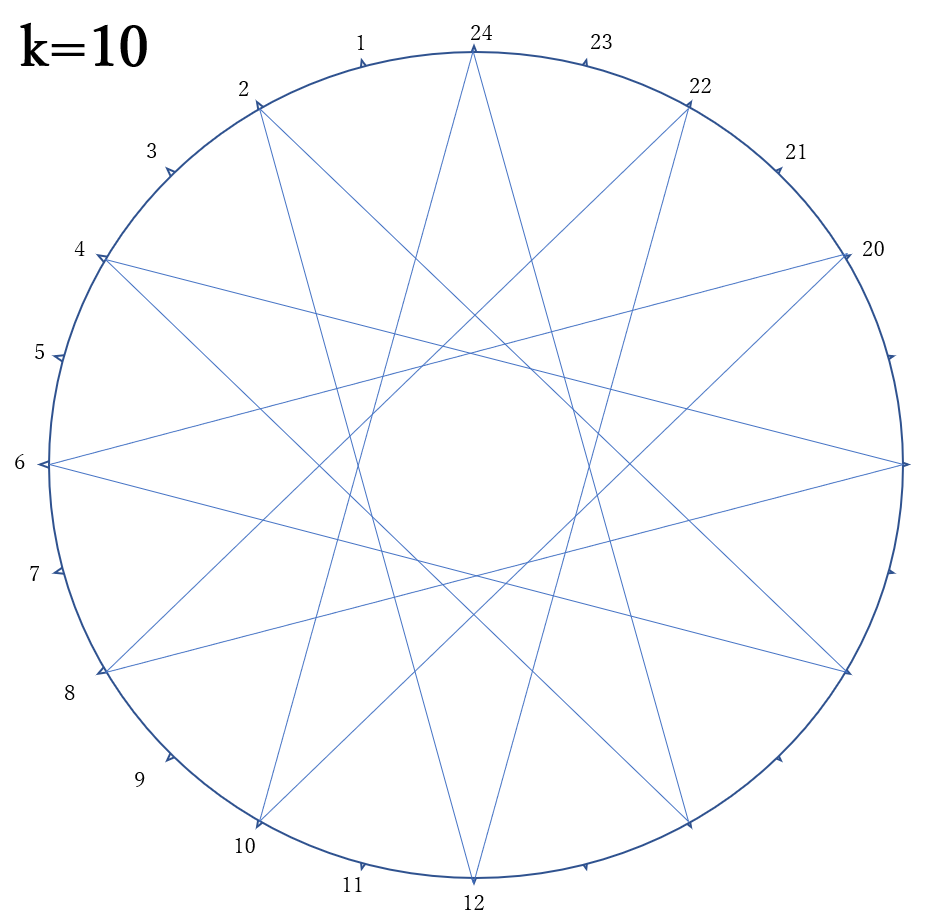
《\(k=10 \ \)のとき》
10と24は互いに素ではありません。10と24の最小公倍数は\( \ 10 \times 12=120 \ \)ですから、12本目の直線を引いたときにスタートの点に戻って、星形正12角形になってしまいます。
右の図
したがって、
星形正24角形を作れる
のは、
\(k\)と24が互いに素
のとき、つまり、
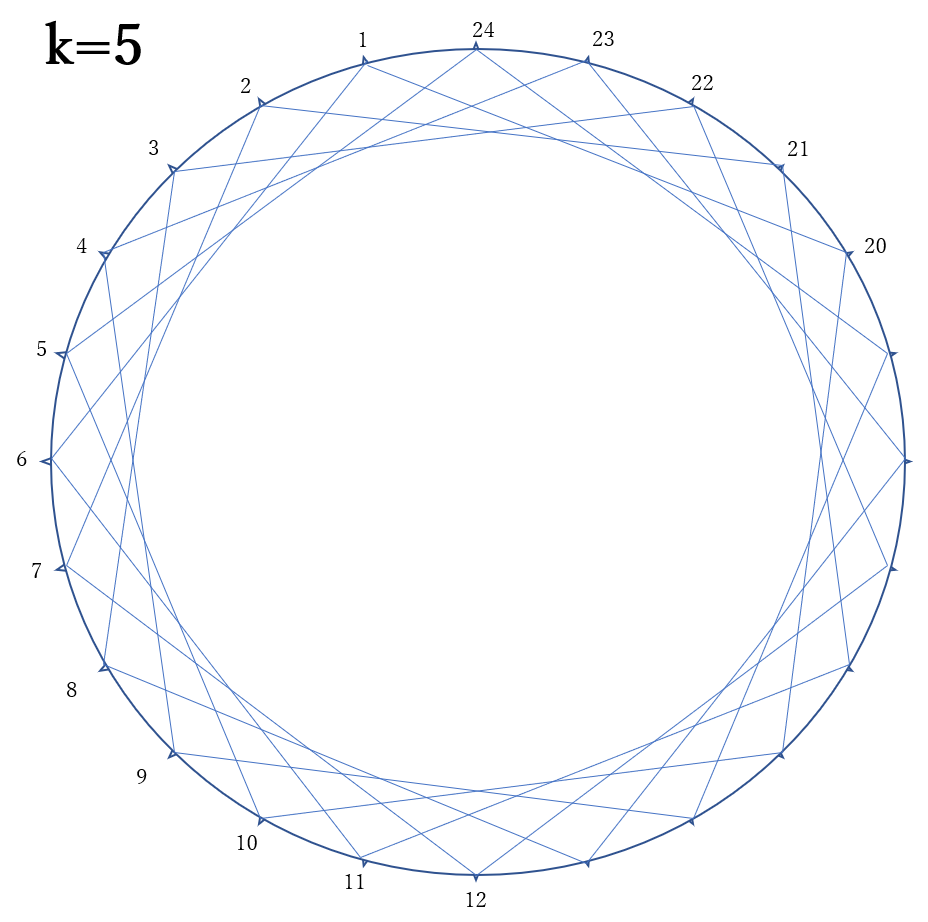
\(k=5,7,11\)のときです。
\(k=5,7,11\)のとき、
星形正24角形をかくことができます。右、下の図
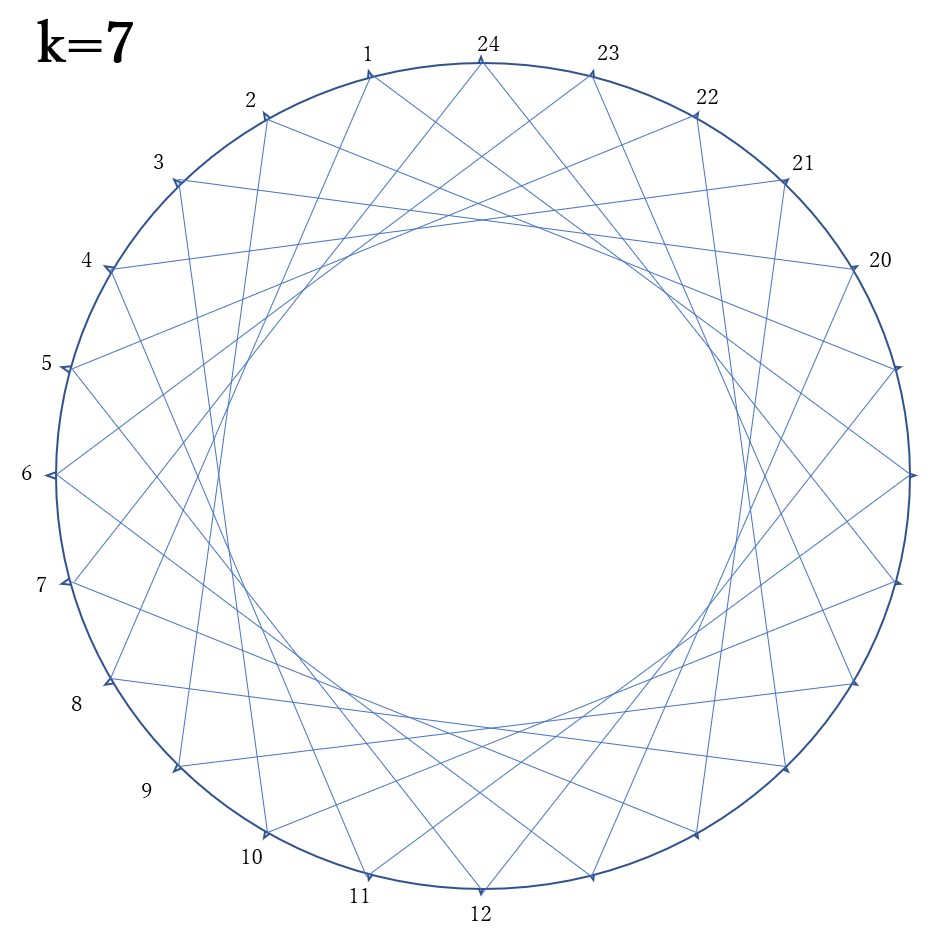
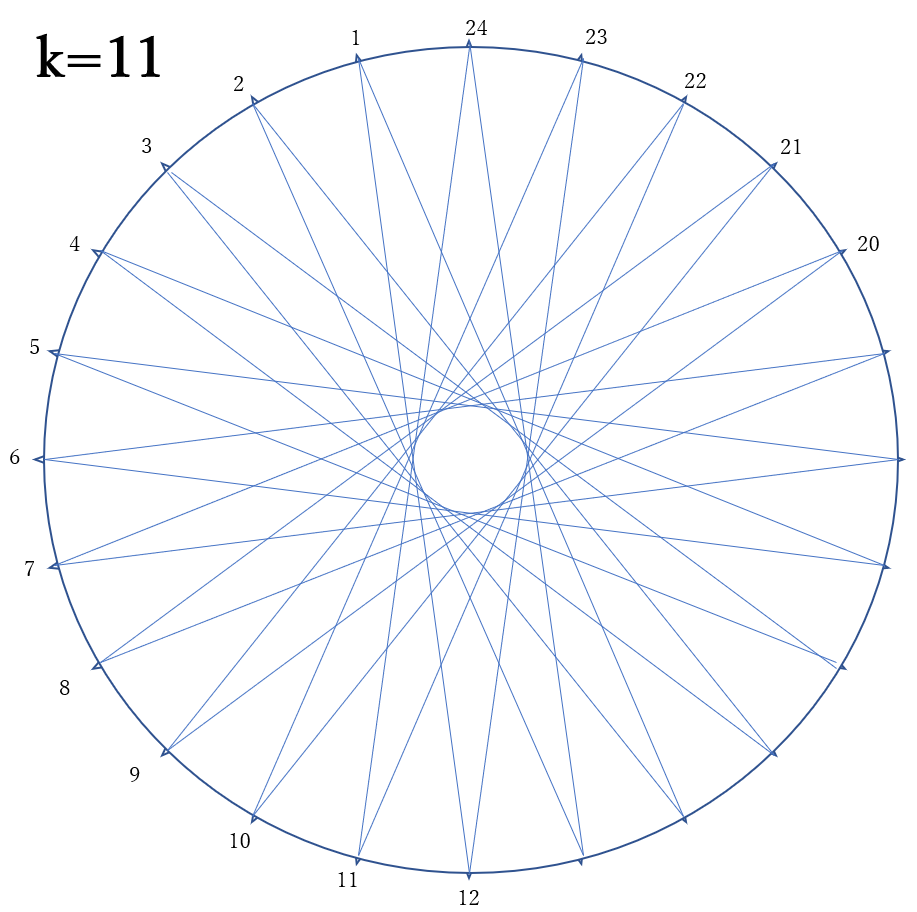

先端部分の角が一番小さくなるのは、11個目ごとに結んだ場合です。11個目ごとに結んでできる星形正24角形の角の大きさは、24等分された円周の2個分の円周角と等しいです。
よって、その中心角は
\(360^{\circ}\times\)\(\large \frac{2}{24}\)\(=360^{\circ}\times \)\(\large \frac{1}{12}\)\(=30^{\circ}\)
ゆえに円周角は\(15^{\circ}\)
(4)(答) 3種類 、 15(度)
追伸
ほとんどの公立中学校では、「互いに素」の意味を教えていないと思います。「約数」とか「最小公倍数」を使って解くことになると思われます。難解で時間がかかる問題です。(3)まで解ければ成功でしょう。
