関東地方の1都6県最後の群馬県である。群馬県の高校入試は、前期試験と後期試験の2回行われている。前期試験は素直で平易な問題ばかりであったので、ここでは後期試験を扱う。
また、扱う問題は、受験生が解法にてこずりそうなものだけを取り上げている。
難解な問題は少ないが、大問5、大問6は少し解答に時間がかかる。大問4まではすんなりと解きたいものだ。
では、大問6(3)から
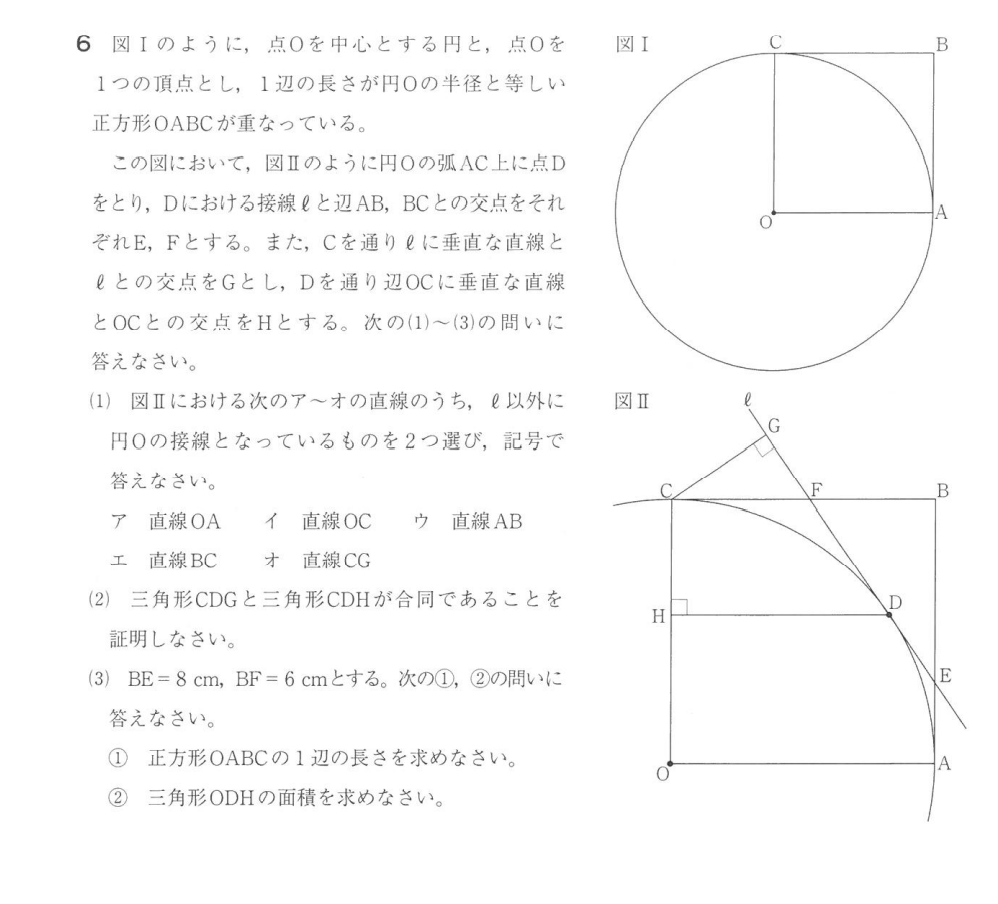
大問6(3)解答例
①
(2)より $$ \triangle CDG \equiv \triangle CDH $$
求める長さを\(x\)とおく
\(CF=x-6, \quad AE=x-8 \)
\(FC\)と\(FD\)は円\(O\)の接線だから
\(CF=FD=x-6\) 同様に
\(EA\) と \(ED\) は 円 \(O\) の接線だから
\(EA=ED=x-8\)
\(BE=8, \quad BF=6\) ゆえ
\( \triangle FBE\) は
\(FB:BE:FE=3:4:5\) の直角三角形
したがって \(FE=10\)
\(\iff FE=FD+ED\)
\(=(x-6)+(x-8)=2x-14\)
\( \iff 2x-14=10\)
\( \iff x=12\)
(答) \(12 \ (cm)\)
②
①より \(FE=10, \quad CF=FD=6\)
\(\triangle CGF \sim \triangle EBF\) だから
\( CF:FG=5:3\)
\(\iff 6:FG=5:3\)
\(\iff FG= \frac{18}{5}\)
\(\iff GD=FG+FD=\frac{18}{5}+6=\frac{48}{5}\)
また、\( CF:CG=5:4\)
\(\iff 6:CG=5:4\)
\(\iff CG= \frac{24}{5}\)
(2)より $$ \triangle CDG \equiv \triangle CDH $$だから
\(CH=CG=\frac{24}{5}, \quad HD=GD=\frac{48}{5}\)
\(\iff OH=12-CH=12-\frac{24}{5}=\frac{36}{5}\)
よって求める \(\triangle ODH\) の面積は
\(OH \times HD \times \frac{1}{2}=\frac{36}{5} \times \frac{48}{5} \times \frac{1}{2}\)
\(=\frac{864}{25}\)
(答) \( \displaystyle \frac{864}{25} \quad (cm^2)\)
次は、大問5(2)
この問題は、点\(P\)の相対速度を用いると簡単に解けるが、まずは、普通の解き方でやってみよう。相対速度を用いた解法は、【別解】で示した。
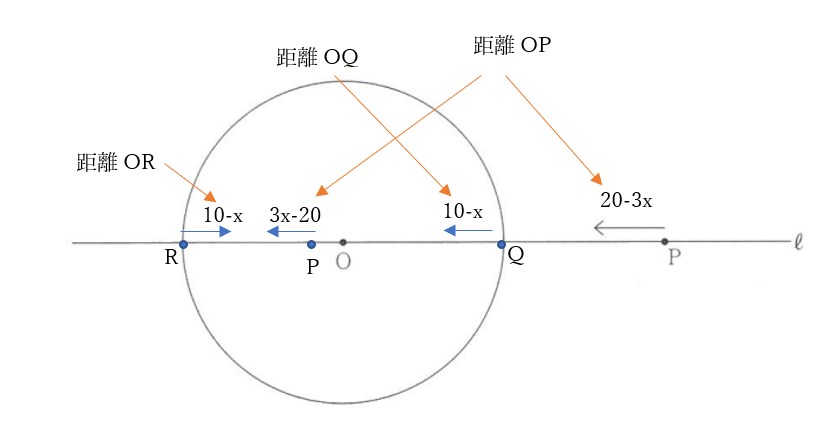
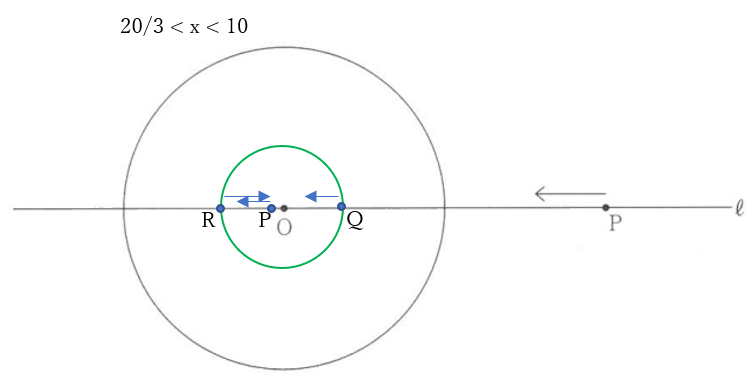
大問5(2)の解答例
右の図のように円\(O\)と直線\(l\)との交点を\(Q,R\)とする。
点 \(P,\quad Q,\quad R\) の動き方を確認しておく
点\(P\)が出発し、円\(O\)の半径が小さくなり始めると、点\(Q,R\)が、毎秒\(1cm\)の速さで点\(O\)に接近し、距離\(OQ,OR\)は短くなっていく。点\(P\)は毎秒\(3cm\)の速さで円\(O\)に近づく。
円\(O\)が小さくなり始めてから\(\frac{20}{3}\)秒までの間に点\(P\)は点\(Q\)に追いつき、\(\frac{20}{3}\)後に点\(P\)は点\(O\)を通り過ぎ、点\(R\)に接近する。
次に計算
\(0 \leq x \leq \frac{20}{3}\)のとき
\(OP=20-3x,\quad OQ=10-x,\quad OR=10-x\)
\(\frac{20}{3} \leq x \leq 10\)のとき
\(OP=3x-20,\quad OQ=10-x,\quad OR=10-x\)
点\(P\)が出発してから点\(Q\)に追いつくまでの時間は、
\(0 \leq x \leq \frac{20}{3}\)のときだから
\(OP=OQ\) より、\(20-3x=10-x\)
\(\iff x=5\) \(5\)秒 である。
点\(P\)が出発してから点\(R\)と重なる時間は、
\(\frac{20}{3} \leq x \leq 10\)のときだから
\(OP=OR\) より、\(3x-20=10-x\)
\(\iff x=\frac{15}{2}\) \(\frac{15}{2}\)秒である。
よって、点\(P\) が 円\(O\) の周上または内部にある時間は
\(\frac{15}{2}-5=\frac{5}{2} \)
(答) \(\displaystyle \frac{5}{2}\) (秒間)
【別解】
点\(P\)の点\(Q, \ R\)に対する相対速度を用いる。
すなわち、点\(Q, \ R\) は、停止していると仮定する。
点\(P\)の点\(Q\)に対する相対速度は、毎秒\(2cm\)
よって、点\(P\)が点\(Q\)に到達する時間は
\(\frac{QP}{2}=\frac{10}{2}=5\)
点\(P\)の点\(R\)に対する相対速度は、毎秒\(4cm\)
よって、点\(P\)が点\(R\)に到達する時間は
\(\frac{RP}{4}=\frac{30}{4}=\frac{15}{2}\)
よって、点\(P\) が 円\(O\) の周上または内部にある時間は
\(\frac{15}{2}-5=\frac{5}{2} \)
(答) \(\displaystyle \frac{5}{2}\) (秒間)
