ここからは中部地方。まずは、静岡県。50分間の試験の割には問題数が多い。難解な問題はないが、思考を要する問題が4,5題出題されているので、ずべてを解くのはかなり難しいと思われる。解法に戸惑う問題はあとまわしにして、とにかく、最後までやり通そう。
思考を要すると思われる問題を抜粋して解答してみよう。
大問2(2)イ

イの解答例
残ったカードの形が2種類になる場合は、①円形と六角形、②六角形と長方形の2通り
①円形と六角形の場合
\(a \leq 2\) かつ \(b \geq 5\) だから、\(\frac{2}{6} \times \frac{2}{6}=\frac{1}{9}\)
②六角形と長方形の場合
\(a \geq 3\) かつ \(b \leq 4\) だから、\(\frac{4}{6} \times \frac{4}{6}=\frac{4}{9}\)
よって、求める確率は、\(\frac{1}{9}+\frac{4}{9}=\frac{5}{9}\)
(答) \(\large \frac{5}{9}\)
大問4

解答例
6月の可燃ごみの排出量を \(x\) 、6月のプラスチックごみの排出量を \(y\) とおく。
5月の可燃ごみの量は、\(x+33 \ kg\)
5月のプラスチックごみの量は、\(y-18 \ kg\)
5月の可燃ごみとプラスチックごみを合わせた総排出量は
\(x+33+y-18=x+y+15\)
6月の総排出量 \(x+y\) は、5月の総排出量より5%減少したから、
\((x+y+15) \times 0.95=x+y\)
\(\iff (x+y+15) \times \frac{19}{20}\)
\(=x+y \quad \cdots \) ①
6月の可燃ごみの排出量は6月のプラスチックごみの排出量の4倍であったから、
\(x=4y \cdots \) ②
①②より、$$ (5y+15) \times \frac{19}{20}=5y $$ $$\iff 19y+57=20y $$ $$ \iff y=57, \quad x=228 $$
(答) 6月の可燃ごみ 228kg、 6月のプラスチックごみ 57kg
大問5(2)(3)
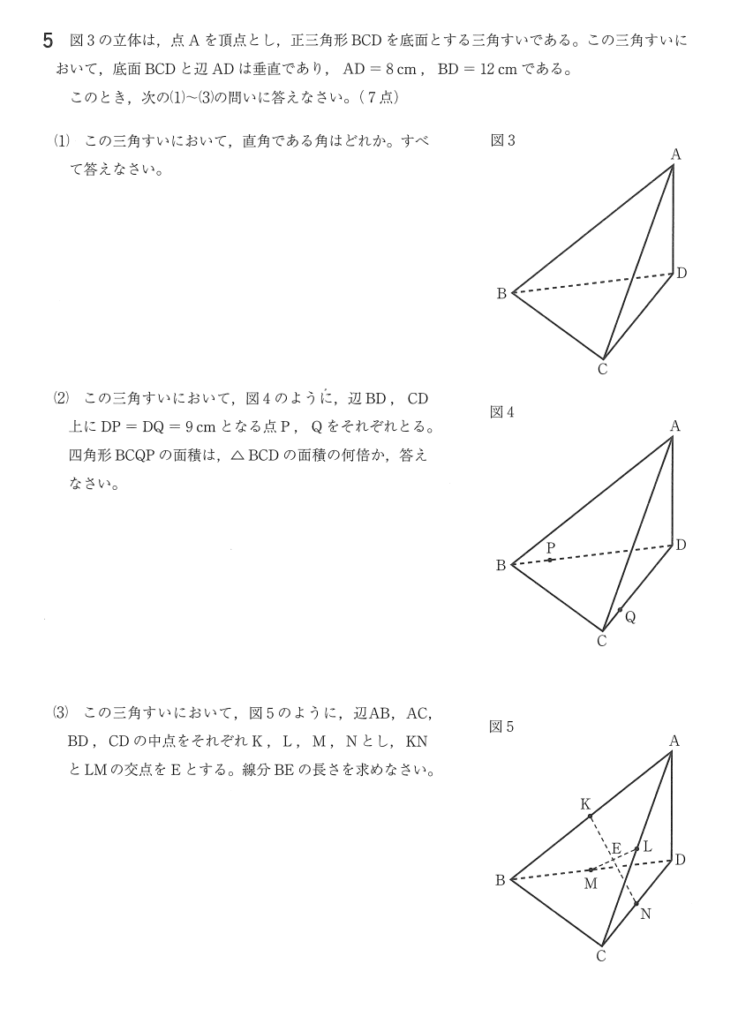
(2)解答例
\(\triangle BCD \sim \triangle PQD\)で、相似比は
\(12:9=4:3\)
よって、面積比は
\(\triangle BCD : \triangle PQD=16:9\)
したがって
四角形\(BCQR\)の面積と
\(\triangle BCD\)の面積比は
四角形\(BCQR:\triangle BCD\)
\(=(16-9):16=7:16\)
よって、四角形\(BCQR\)の面積は
\(\triangle BCD\)の面積の\(\frac{7}{16}\)倍
(答) \( \large \frac{7}{16}\)倍
(2)解答例
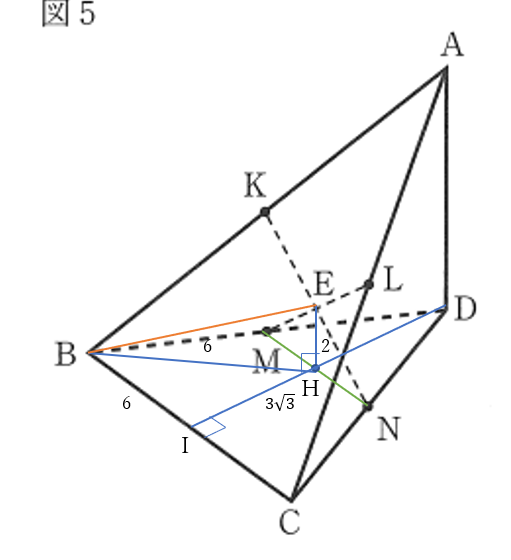
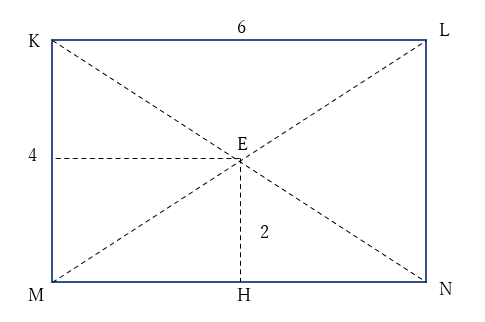
右下の図のように、四角形\(KMNL\)は長方形で
\(KM=4,KL=6\)
点\(E\)から線分\(MN\)に下した垂線の足を\(H\)、\(H\)から辺\(BC\)に下した垂線の足を\(I\)とすると
\(EH=2,BI=6,HI=3\sqrt{3}\)
したがって、
\(BE=\sqrt{BH^2+EH^2}=\sqrt{HI^2+BI^2+EH^2}\)
\(=\sqrt{(3\sqrt{3})^2+6^2+2^2}=\sqrt{27+36+4}=\sqrt{67}\)
(答) \(\sqrt{67}\) \((cm)\)
大問6
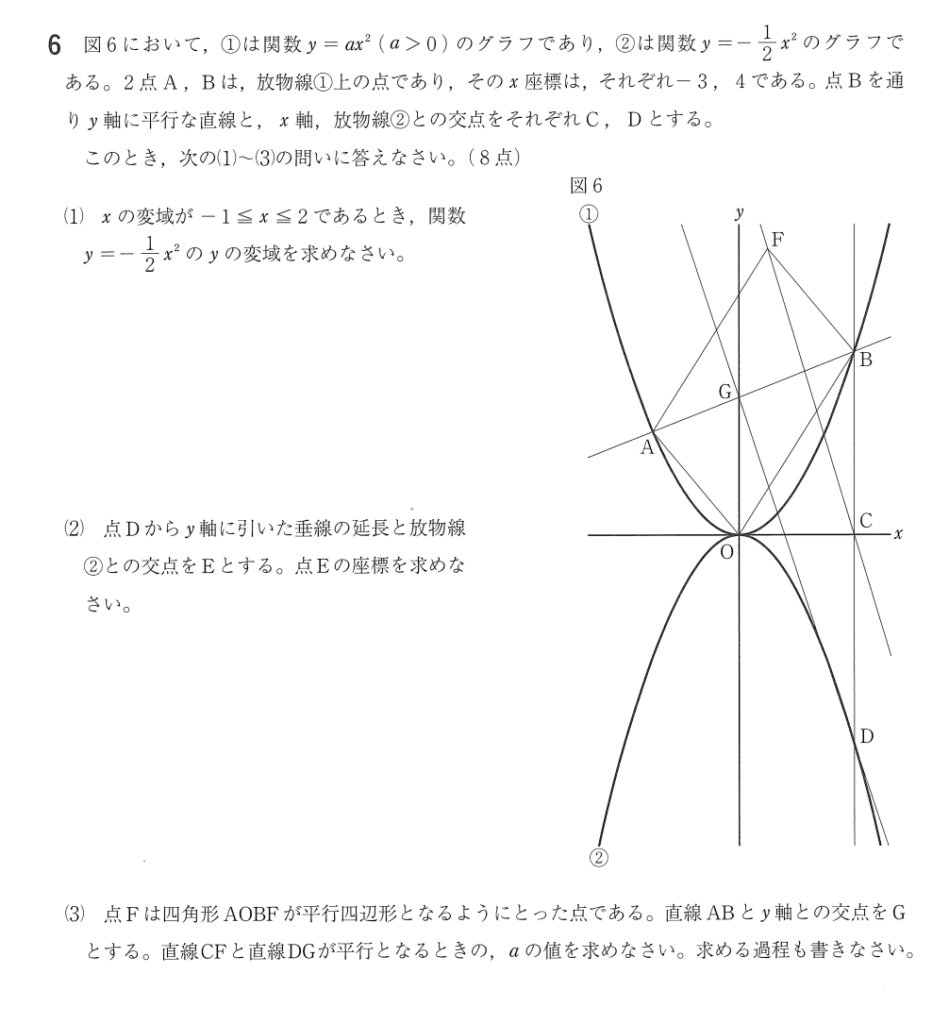
大問6(3)解答例
右下の図のように、点\(A,B,C,D\)の座標は
\(A(-3,9a),B(4,16a),C(4,0),D(4,-8)\)
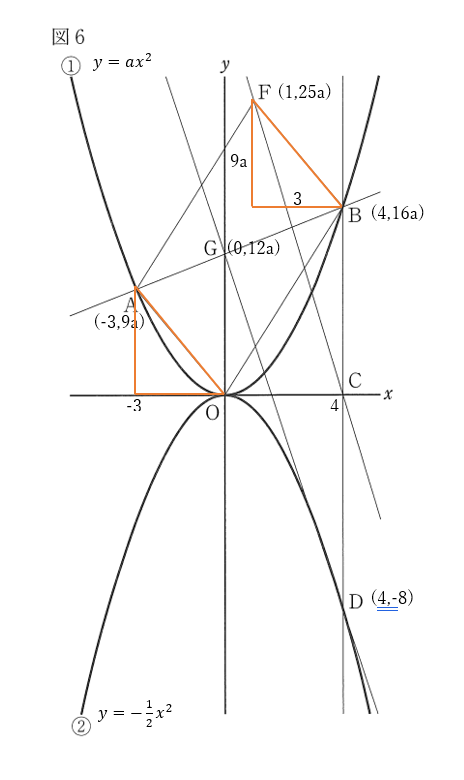
線分\(AB\)の方程式は、
\(y=ax+12a\)
線分\(AB\)と\(y\)軸との交点\(G\)の座標は
\(G(0,12a)\)
\(AO // FB,AO=FB\) より、点\(F\)の座標は
\(F(1,25a)\)
直線\(CF\)の傾きは
\(\frac{-25a}{3}\)
直線\(DG\)の傾きは
\(\frac{-8-12a}{4}\)
\(CF//DG\)より
\(\frac{-25a}{3}=\frac{-8-12a}{4}\)
\(\iff
-100a=-24-36a\)
\( \iff 64a=24\)
\(\iff a=\frac{3}{8}\)
(答) \( \large \frac{3}{8}\)
大問7

大問7 解答例
(1) \(\triangle BOE \equiv \triangle DOG\) の証明
\(\angle OAC=\angle CAD=a\) とおく
(右下の図で、\(\bullet =a, \quad \bullet \bullet=2a\) である)
弧に対する円周角より、
\(\angle CAD=\angle CBD\)
\(=\angle CFD=a\cdots\) ①
\(\triangle OAC\) は二等辺三角形だから
\(\angle OAC=\angle OCA=a\)
円周角と中心角の関係より
\(\angle BOA=2\angle OCA=2a \cdots\)②
\(\angle COD=2\angle CFD=2a \cdots\)③
錯角より
\(\angle CFD=\angle ODF=a \cdots\)④
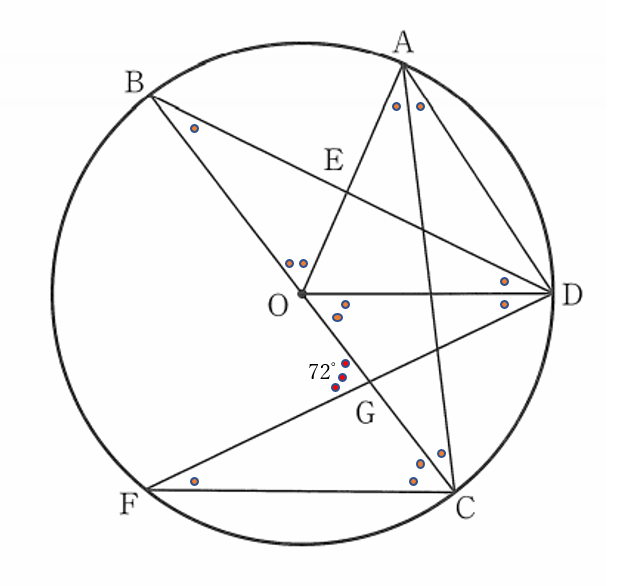
①②③④より、
\(\triangle BOE\)と\(\triangle DOG\)において
\(\angle OBE=\angle ODG=a \cdots\)⑤
\(\angle BOE=\angle DOG=2a \cdots\)⑥
\(OB,OD\)は円\(O\)の半径だから
\(OB=OD \cdots\)⑦
⑤⑥⑦より、一辺とその両端の角が等しいから
\(\triangle BOE \equiv \triangle DOG\)
(3) 解答例
(1)より
\(\angle BGF=\angle DOG + \angle ODG\)
\(=2a+a=3a\)
\(\iff 3a=72^{\circ}\)
\(\iff a=24^{\circ}\)
\(\iff 2a=48^{\circ}\)
よって(1)より
\(\angle AOD=180^{\circ}-\angle BOE-\angle DOG\)
\(=180^{\circ}-2a-2a\)
\(=180^{\circ}-4a\)
\(=180^{\circ}-96^{\circ}\)
\(=84^{\circ}\)
したがって、
\(\stackrel{\huge\frown}{AC}=2\pi \times 6 \times \frac{84^{\circ}}{360^{\circ}}\)
\(=\frac{14}{5}\pi\)
(答) \(\large \frac{14}{5}\pi\)
