思考を要する問題がいくつか出題されています。大問6⃣(3)はやや難解ですが、良問です。計算が簡単になるように解く必要がありますが、気がつかないと計算に苦労します。
思考を要すると思われる問題を抜粋して解答しました。
貴重な資料をご提供くださった、福岡県教育庁高校教育課様には心より御礼申し上げます。
なお、この解答例は、本事業所が独自に作成したものであり、福岡県高校教育課において責任を負うものではありません。
大問4⃣
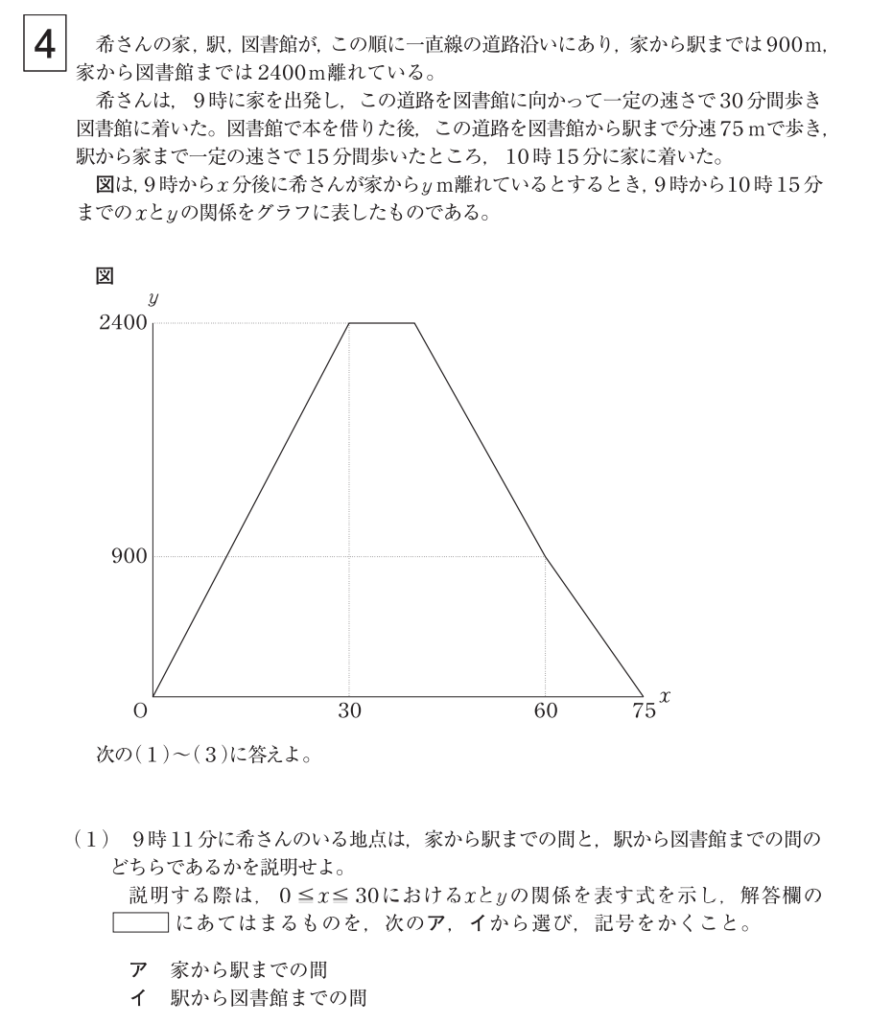

(3)解答例
題意より、希さんの兄が走った時間は
\(38-5-25=18\)
で、18分
走った距離は家から駅までの往復1800mである。
したがって、走った速さは、分速100mである。
希さんの兄が希さんとすれ違うのは家から駅に向かう時だから
希さんの兄の\(x\)と\(y\)の関係式は
\(y=100x-6500 \ ,\quad (65 \leq x \leq 74) \cdots\)①
希さんは駅から家まで15分間歩いたので
その速さは分速60m。
よって、10時以降の希さんの\(x\)と\(y\)の関係式は
\(y=-60x+4500 \cdots\)②
①②より
\(x=68.75\)
よって求める時刻は、10時8分45秒
(3)(答) 10時8分45秒
大問5⃣
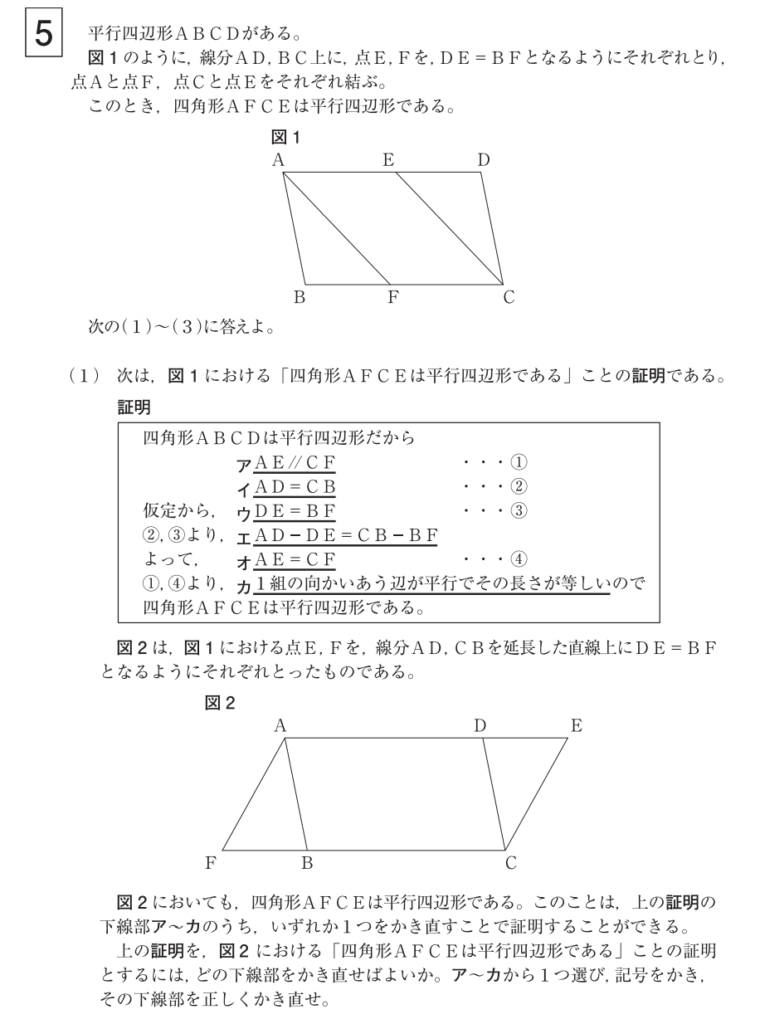
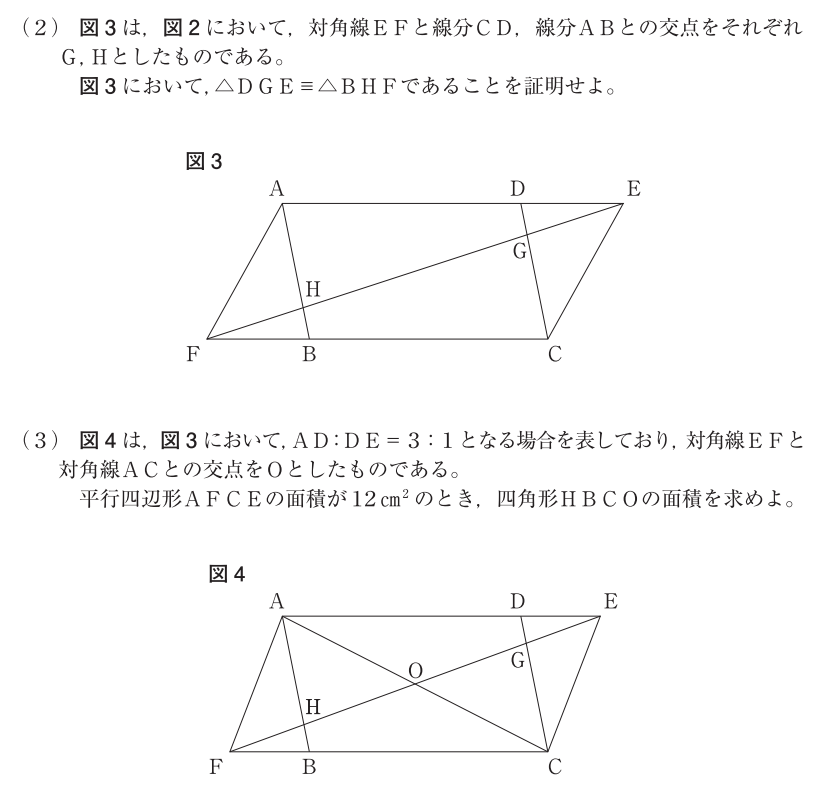
(3)解答例
《考え方》
四角形\(HBCO=\triangle OFC-\triangle HBF\)
・・・・・・・・・・・・・・・・・・・・
\(\triangle GDE \equiv \triangle HBF\)ゆえ
\(DE=BF \iff AD:FB=3:1\)
\(\iff AE:BF=4:1\)
\(\triangle HAE \sim \triangle HBF\)だから
\( AE:BF=AH:BH=4:1\)
\(\iff \triangle HBF=\frac{1}{5} \triangle AFB \cdots\)①
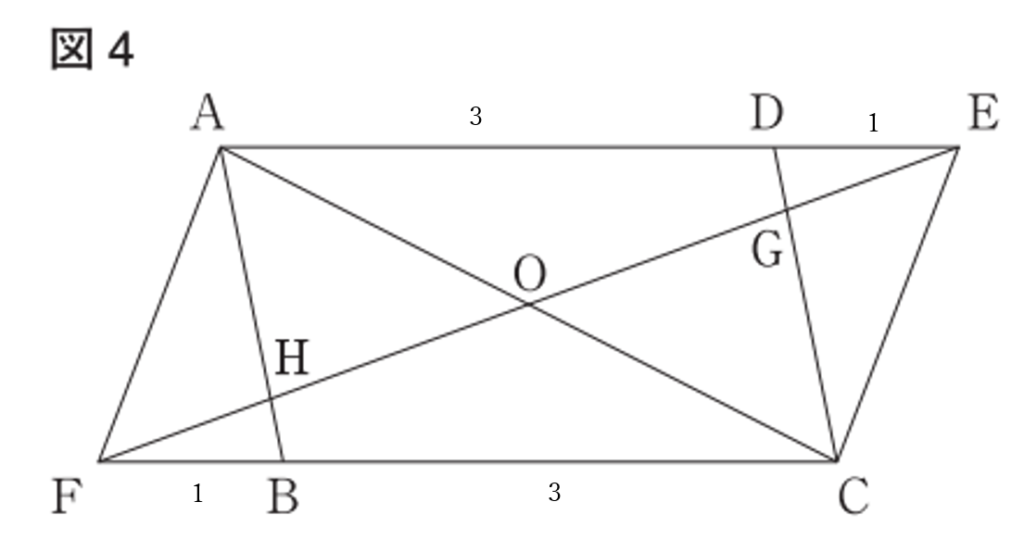
\(\triangle AFB\)の面積は
\(FB:BC=1:3\)より
\(\triangle AFB=\triangle AFC \times \frac{1}{4}\)
\(=\frac{1}{2}\)平行四辺形\(AFCE\times \frac{1}{4}\)
\(=6 \times \frac{1}{4}=\frac{3}{2}\cdots\)②
①②より
四角形\(HBCO=\triangle OFC-\triangle HBF\)
\(=\frac{1}{2}\triangle AFC-\frac{1}{5}\triangle AFB\)
\(=\frac{1}{2}(\frac{1}{2}\)平行四辺形\(AFCE)-\frac{1}{5} \cdot \frac{3}{2}\)
\(=\frac{1}{2} \cdot \frac{1}{2} \cdot 12-\frac{3}{10}\)
\(=3-\frac{3}{10}=\frac{27}{10}\)
(3)(答) \(\large \frac{27}{10}\) \((cm^2)\)
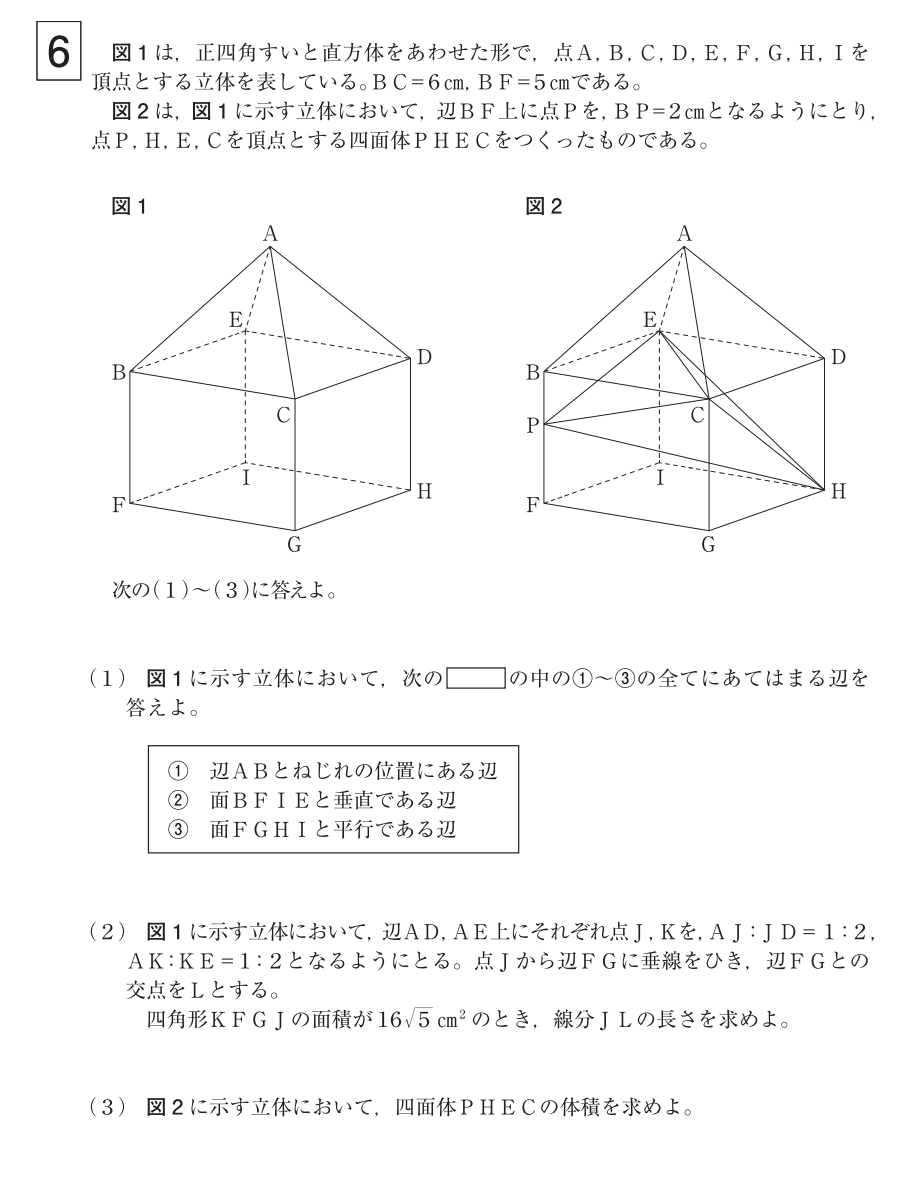
大問6⃣
(2)解答例
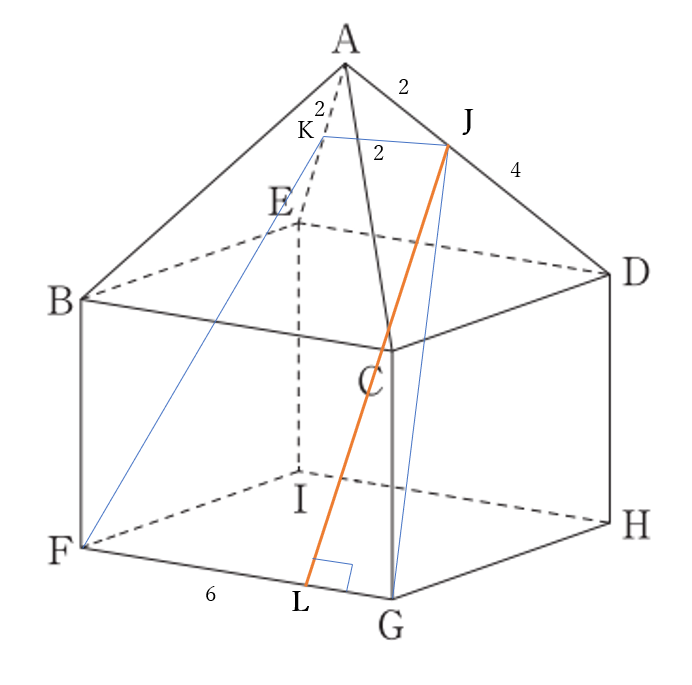
\(AJ:JD=1:2\)
\(AK:KE=1:2\) より
\(AJ=2, \quad JD=4\)
\(AK=2, \quad KE=4\)
\(\triangle AKJ\)は、正三角形だから
\(KJ=2, \quad KJ//FG\)
よって四角形\(KFGJ\)は台形だから
\(\frac{1}{2}(2+6)JL=16\sqrt{5}\)
\(\iff JL=4\sqrt{5}\)
(2) (答) \(4\sqrt{5}\) \((cm)\)
(3)解答例
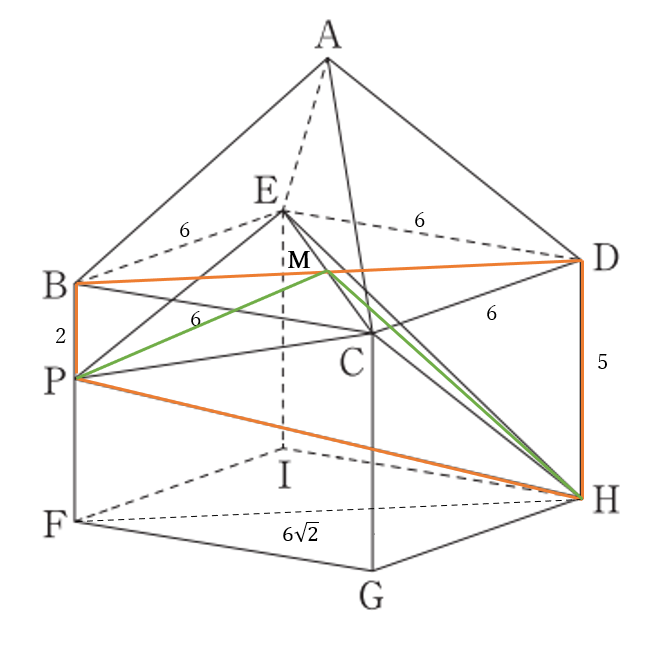
解答例を3つ示しますが、【解答例1】と【解答例2】はほとんど同じです。【解答例3】は計算が複雑になってしまうので、あまりお勧めできません。
【解答例1】
《考え方》
線分\(BD\)と線分\(EC\)との交点を\(M\)とおく
四面体\(PHCE\)を平面\(BPHD\)で切ったときにできる二つの三角錐\(C-MPH\)、\(E-MPH\)を考える。
三角錐\(C-MPH\)と三角錐\(E-MPH\)は合同である。
したがって、
三角錐\(C-MPH=\)三角錐\(E-MPH\)
である。
・・・・・・・・・・・・・・・・・・・・
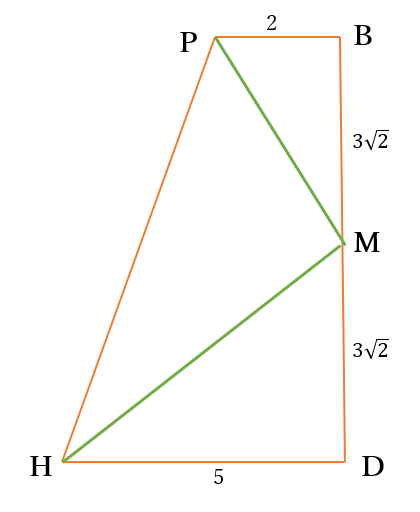
\(\triangle MPH\)の面積は
台形\(BPHD-\triangle BMP-\triangle DMH\)
\(=21\sqrt{2}-3\sqrt{2}-\frac{15}{2}\sqrt{2}\)
\(=\frac{21}{2}\sqrt{2}\)
よって、三角錐\(C-MPH\)の体積は
\(\frac{21}{2}\sqrt{2} \times 3\sqrt{2} \times \frac{1}{3}\)
\(=21\)
ゆえに求める四面体\(PHCE\)の体積は
\(21\times 2=42\)
(3)(答) \(42\) \((cm^3)\)
【解答例2】
《考え方》
右の図のように
台形\(BPHD\)を底辺、\(C\)を頂点とした
四角錐\(C-BPHD\)を考える。
この四角錐を二つ合わせた
立体\(CBPHDE\)から
三角錐\(C-BPE\) と
三角錐\(C-HDE\) を
取り除いた立体が求める
四面体\(PHCE\)である。
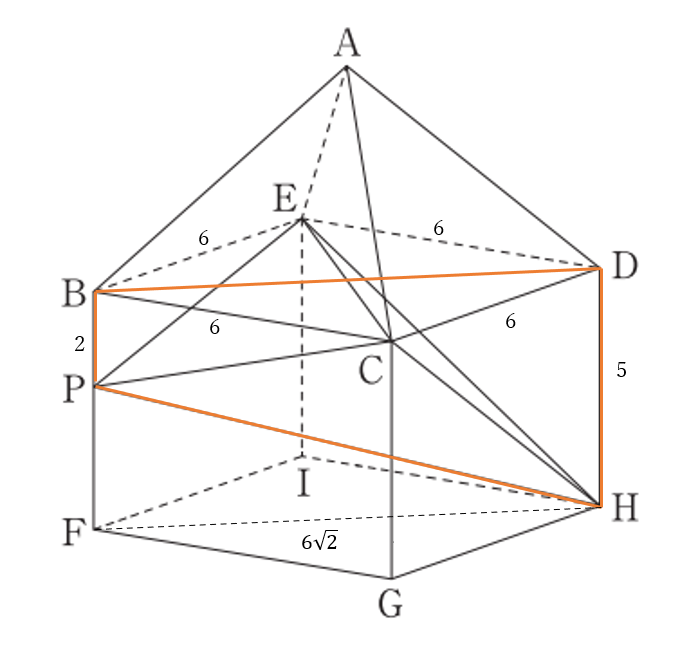
・・・・・・・・・・・・・・・・・・・・
台形\(BPHD\)を底辺、\(C\)を頂点とした
四角錐\(C-BPHD\)の体積は
\((BP+DH)FH\times \frac{1}{2}\times \frac{1}{2}CE\times \frac{1}{3}\)
\(=(2+5)\cdot 6\sqrt{2}\cdot \frac{1}{2}\times 3\sqrt{2}\times \frac{1}{3}\)
\(=42\)
よって、この四角錐を二つ合わせた
立体\(CBPHDE\)の体積は
\(42\times 2=84\)
三角錐\(C-BPE\)の体積は
\(6\times 2\times \frac{1}{2} \times 6\times \frac{1}{3}\)
\(=12\)
三角錐\(C-HDE\)の体積は
\(6\times 5\times \frac{1}{2}\times 6\times \frac{1}{3}\)
\(=30\)
ゆえに、求める四面体\(PHCE\)の体積は
\(82-12-30=42\)
(3)(答) \(42\) \((cm^3)\)
【解答例3】
《考え方》
四面体\(PHCE\)を
\(\triangle PCE\)を底面、\(H\)を頂点とする三角錐\(H-PCE\)と考える。
・・・・・・・・・・・・・・・・・・
\(\triangle PCE\)は\(PC=PE\)の二等辺三角形
右の図のように、
\(P\)から線分\(CE\)に下した垂線の足を\(M\)とおく
点\(P,H,D,M\)は同一平面上にあるので、
直線\(PM\)と直線\(DH\)は1点で交わる。
直線\(PM\)と直線\(DH\)の交点を\(Q\)とおくと
\(DQ=2\)
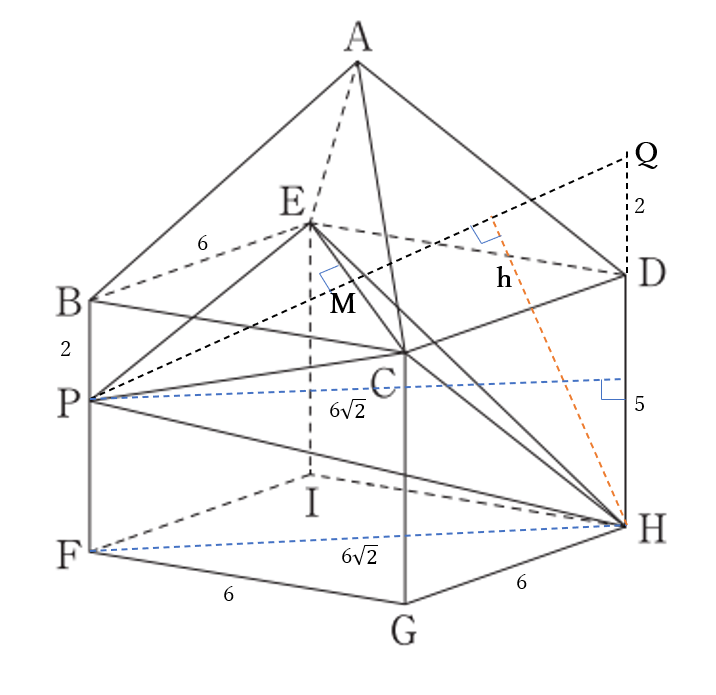
頂点\(H\)から直線\(PQ\)に下した垂線の長さが、三角錐\(H-PCE\)の高さである。
右図のように
頂点\(H\)から直線\(PQ\)に下した垂線の長さを\(h\)とおく
\(\triangle PHQ\)の面積は
\(HQ\times FH \times \frac{1}{2}\)
\(=7\times 6\sqrt{2}\times \frac{1}{2}=21\sqrt{2}\cdots\)①
\(\triangle PHQ\)において
\(PQ \times h \times \frac{1}{2}\cdots\)②
も\(\triangle PHQ\)の面積である
ここで
\(PM=\sqrt{PE^2-EM^2}\)
\(=\sqrt{BP^2+BE^2-(\frac{1}{2}CE)^2}\)
\(=\sqrt{2^2+6^2-(3\sqrt{2})^2}\)
\(=\sqrt{22}\)
\(\iff PQ=2\sqrt{22}\cdots\)③
①②③より
\(PQ \times h \times \frac{1}{2}=21\sqrt{2}\)
\(\iff 2\sqrt{22} \ h\times \frac{1}{2}=21\sqrt{2}\)
\(\iff h=\large \frac{21\sqrt{2}}{\sqrt{22}}=\frac{21}{\sqrt{11}}\)
よって求める四面体\(PHCE\)の体積は
\(\triangle PCE \times h \times \frac{1}{3}\)
\(=CE\cdot PM \cdot \frac{1}{2} \times \large \frac{21}{\sqrt{11}}\times \frac{1}{3}\)
\(=6\sqrt{2}\cdot \sqrt{22} \cdot \frac{1}{2}\cdot \large \frac{21}{\sqrt{11}} \cdot \frac{1}{3}\)
\(=42\)
(3)(答) \(42\) \((cm^3)\)