三重県では前期と後期の2回試験が行われる。まず、前期試験から。全体的に基本的で解きやすい問題であるが、面積問題が多く出題されており、大問4、大問5の面積問題に少し時間を要するかもしれない。
大問3
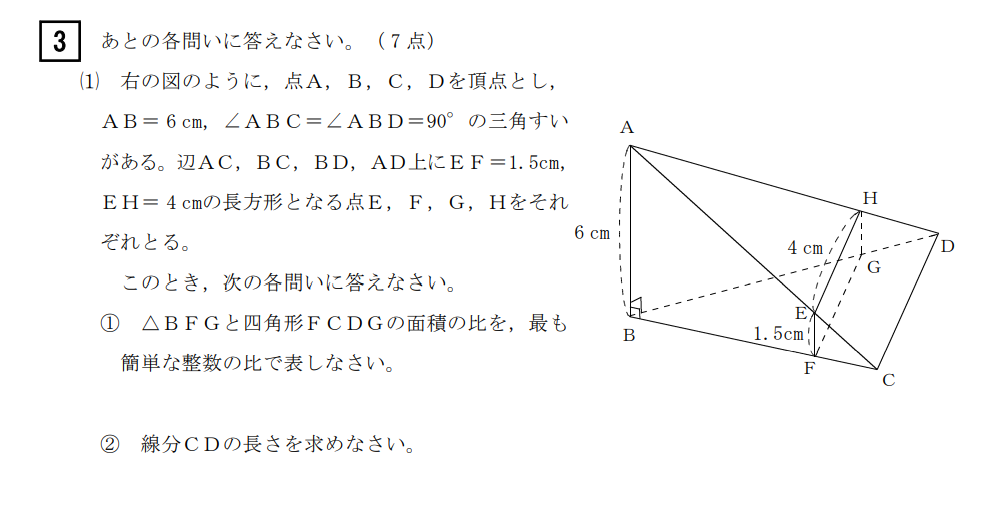
(1)解答例
①
\(AB:EF=6:1.5=4:1\)
\( \iff BC:FC=4:1 \)
\(\iff BC:BF=4:3\cdots \ (\ast)\)
したがって、
\(\triangle BFG\)と\(\triangle BCD\)の面積比は
\(\triangle BFG : \triangle BCD\)
\(=3^2:4^2=9:16\)
よって\(\triangle BFG\)と四角形\(FCDG\)の面積比は
\(\triangle BFG :\)四角形\(FCDG\)
\(=\triangle BFG : (\triangle BCD-\triangle BFG)\)
\(=9:(16-9)=9:7\)
① (答) \(9:7\)
②
\((\ast)\)より\(CD:FG=4:3\)
\(\iff CD=\frac{4}{3}FG\)
\(=\frac{4}{3} \times 4=\frac{16}{3}\)
② (答) \(\large \frac{16}{3}\) \((cm)\)
大問4

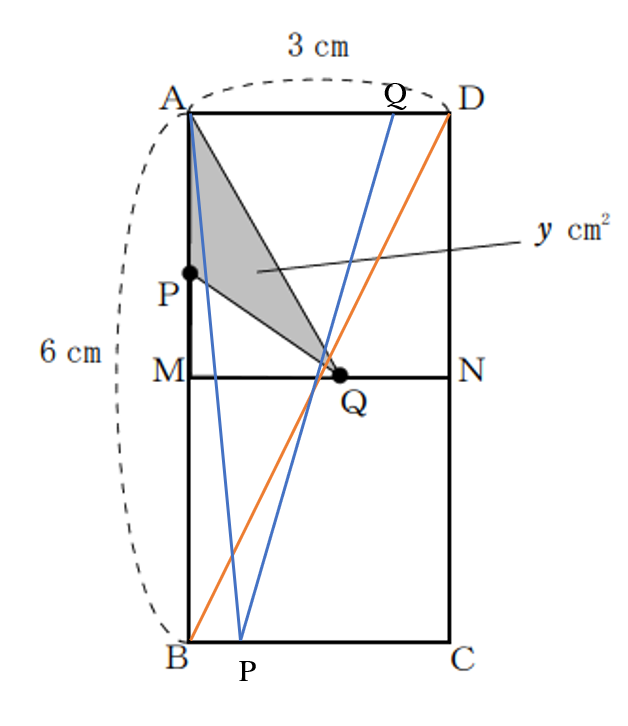
(3)解答例
(ⅰ)\(0 \leq x \leq 3\) のとき
\(y=\frac{1}{2}x^2\)
(ⅱ)\(3 \leq x \leq 6\) のとき
\(y=\frac{3}{2}x\)
(ⅲ)\(6 \leq x \leq 9\) のとき
\(y=-3x+27\)
以上の3つの場合について最大値を求めると
(ⅰ)\(0 \leq x \leq 3\) のとき
\(y\) は増加関数なので
\(x=3\)のとき最大値\(y=\frac{9}{2}\)
(ⅱ)\(3 \leq x \leq 6\) のとき
\(y\) は増加関数なので
\(x=6\)のとき最大値\(y=9\)
(ⅲ)\(6 \leq x \leq 9\) のとき
\(y\) は減少関数なので
\(x=6\)のとき最大値\(y=9\)
(3) (答) \(9\) \((cm^2)\)
(4)解答例
(ⅰ)のとき
\(\triangle BNP=\frac{3}{2}(6-x)\)
\(\triangle APQ=\triangle BNP\) より
\(\frac{1}{2}x^2=\frac{3}{2}(6-x)\)
\(\iff (x+6)(x-3)=0\)
\(\iff x=3\)
(ⅱ)のとき
\(\triangle BNP=\frac{3}{2}(6-x)\)
\(\triangle APQ=\triangle BNP\) より
\(\frac{3}{2}x=\frac{3}{2}(6-x)\)
\(\iff x=3\)
(ⅲ)のとき
\(\triangle BNP=\frac{3}{2}(x-6)\)
\(\triangle APQ=\triangle BNP\) より
\(-3x+27=\frac{3}{2}(x-6)\)
\(\iff x=8\)
(5) (答) \(x=3 \ , \quad 8\)
大問5
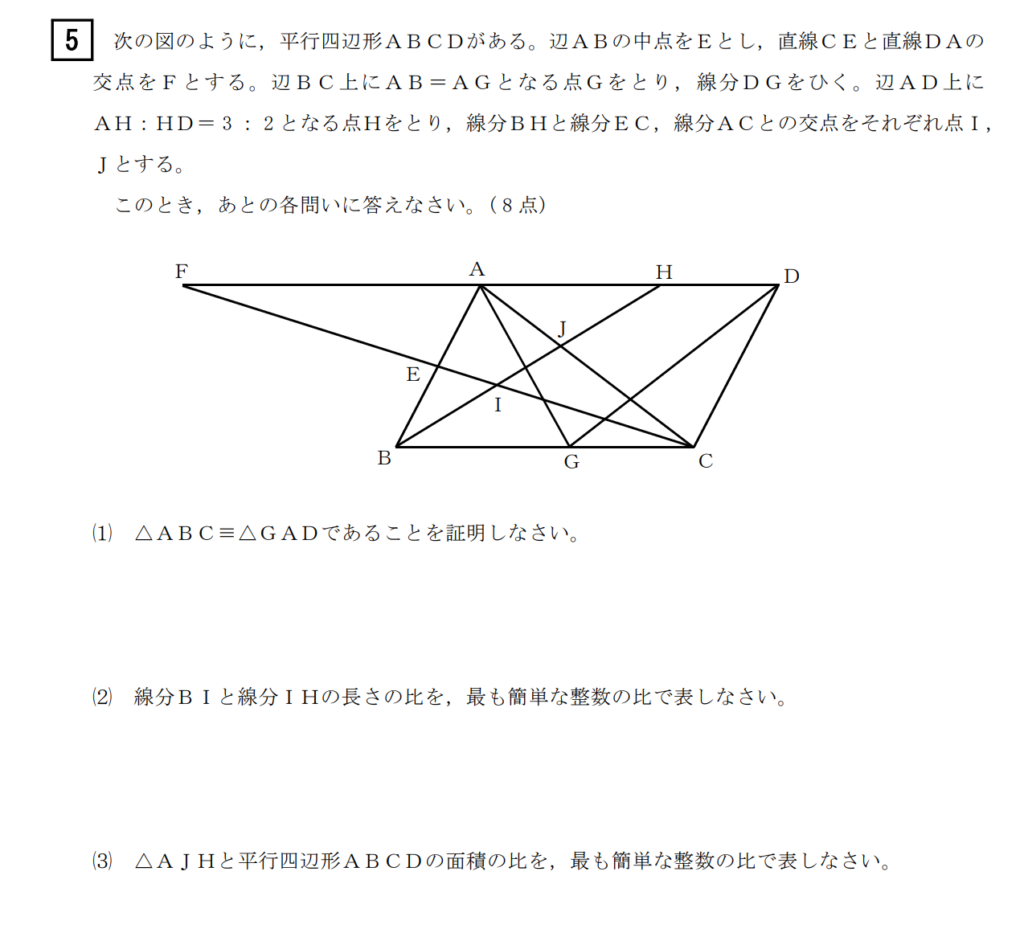
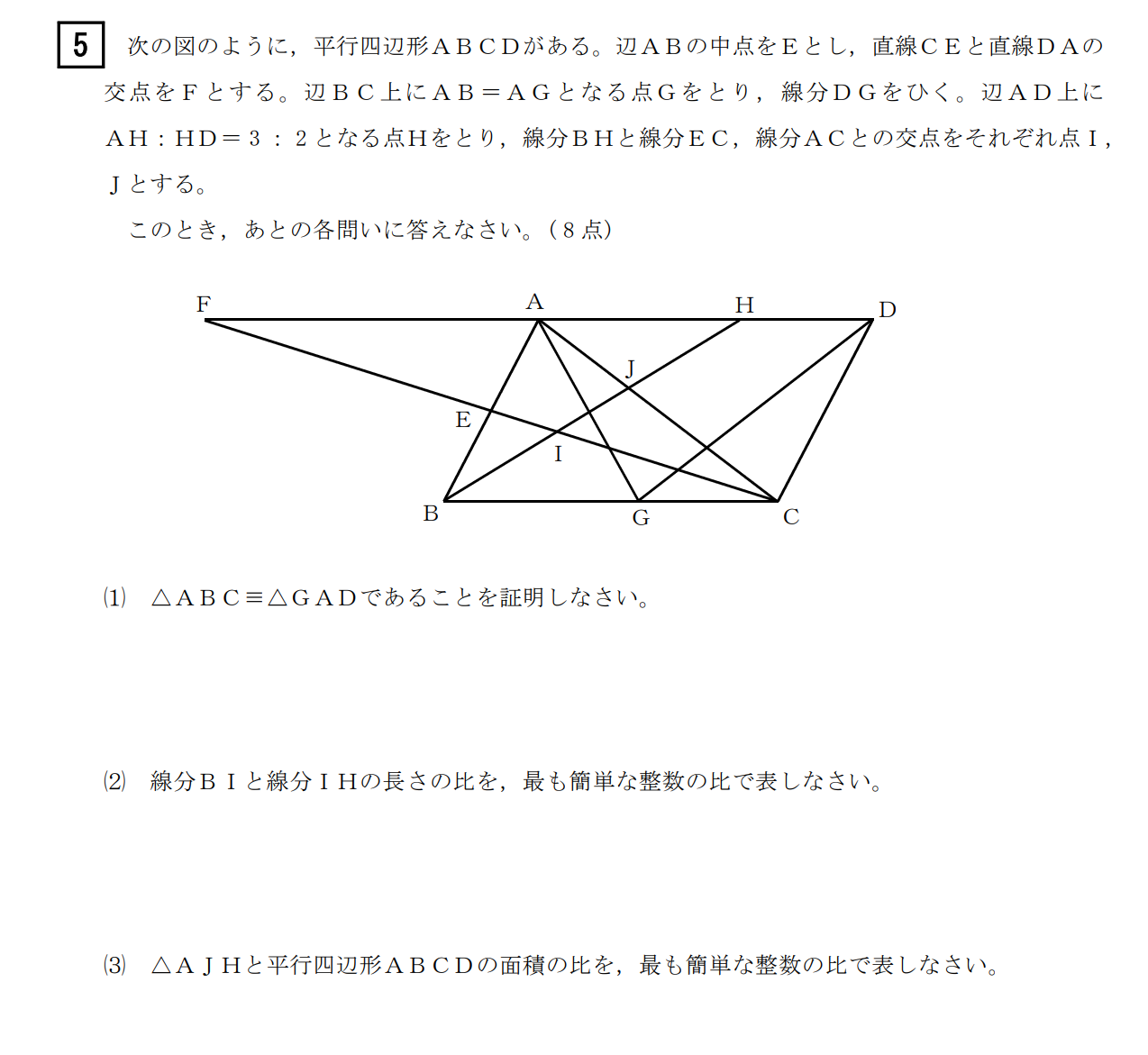
(3)解答例
辺の比や相似比だけで次の順番で計算していく
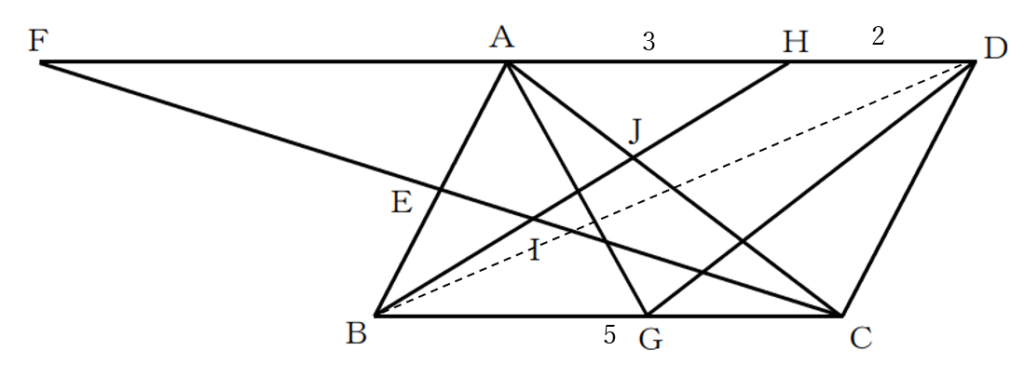
平行四辺形\(ABCD\)
\(\rightarrow \triangle ABC \rightarrow \triangle JBC \rightarrow \triangle AJH\)
平行四辺形\(ABCD\times \frac{1}{2}\times \frac{5}{8}\times (\frac{3}{5})^2\)
\(=\)平行四辺形\(ABCD \times \frac{9}{80}\)
\(=\triangle AJH\)
または
平行四辺形\(ABCD\)
\(\rightarrow \triangle ABD \rightarrow \triangle ABH \rightarrow \triangle AJH\)
の順で
平行四辺形\(ABCD\times \frac{1}{2}\times \frac{3}{5}\times \frac{3}{8}\)
\(=\)平行四辺形\(ABCD \times \frac{9}{80}\)
\(=\triangle AJH\)
(3)(答)
\(\triangle AJH :\) 平行四辺形\(ABCD\)
\(=9:80\)
【別解】
右の図のように、\(J\)を通り、直線\(AD,BC\)に垂直な直線を引き、直線\(AD,BC\)との交点をそれぞれ\(K,L\)とする。

\(\triangle AHJ \sim \triangle CBJ\)
\(AH:HD=3:2\)
より
\(AH:CB=JK:JL=3:5\)
\(\iff JK:KL=3:8\)
\(\iff JK=\frac{3}{8}KL\)
また \(AH:AD=3:5\) だから
\(\triangle AJH=\frac{1}{2}\cdot AH\cdot JK\)
\(=\frac{1}{2}\cdot \frac{3}{5}AD\cdot \frac{3}{8}KL\)
\(=\frac{1}{2}\cdot \frac{3}{5}\cdot \frac{3}{8} AD\cdot KL\)
\(=\frac{9}{80}AD\cdot KL\)
\(=\frac{9}{80} \times\)平行四辺形\(ABCD\)
ゆえに \(\triangle AJH :\)平行四辺形\(ABCD=9:80\)
(答) \(9:80\)