なかなか面白い問題が多い。大問5(3)の線分の長さを求める図形問題は、難解かもしれない。
大問2
大問2(2)解答例
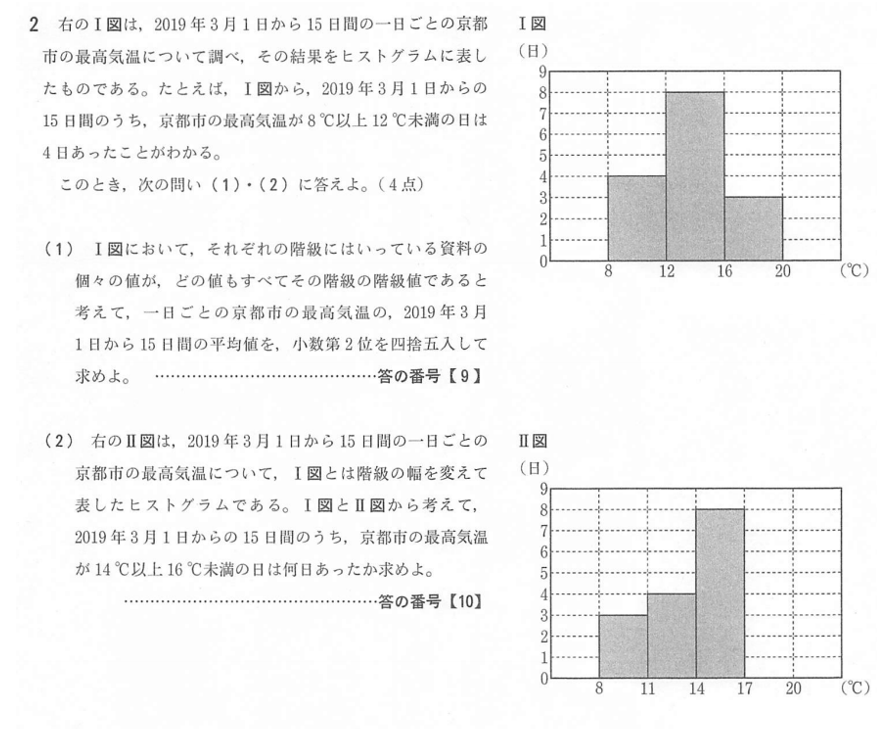
二つの異なる階級の幅のヒストグラム。この二つを比較することによって問題を解かせる内容で、他にあまり類を見ない。
Ⅰ図とⅡ図の比較から、Ⅰ図\(8^{\circ}C\)以上\(12^{\circ}C\)未満の4日の中に、Ⅱ図\(8^{\circ}C\)以上\(11^{\circ}C\)未満の3日が含まれているので、\(11^{\circ}C\)以上\(12^{\circ}C\)未満は1日である。
したがって、Ⅱ図\(11^{\circ}C\)以上\(14^{\circ}C\)未満の4日の中の\(12^{\circ}C\)以上\(14^{\circ}C\)未満は、3日である。
したがって、
Ⅰ図\(12^{\circ}C\)以上\(16^{\circ}C\)未満の8日の中に\(12^{\circ}C\)以上\(14^{\circ}C\)未満の3日が含まれているので、\(14^{\circ}C\)以上\(16^{\circ}C\)未満は、5日である。
(2) (答) 5日
大問3

(2)解答例
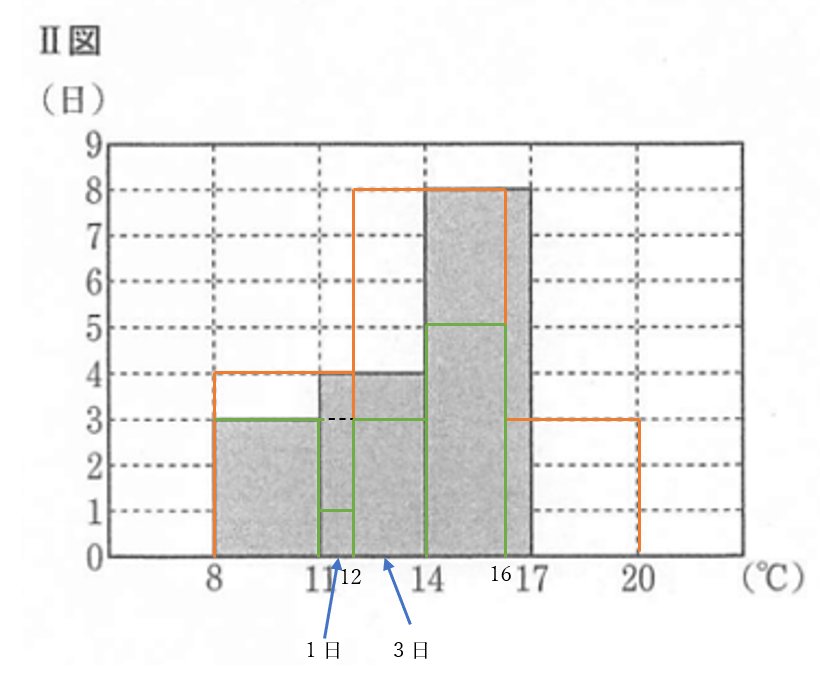
側面の三角形について。
高さが\(3\sqrt{3}cm\)ではない。また、三辺ともに\(6cm\)ではない。
側面の三角形の高さを求める。
右下の図のように、正四角錐の頂点を\(A\)、一つの側面の三角形を\(ABC\)、\(A\)から底面に下した垂線の足を\(H\)、\(A\)から辺\(BC\)に下した垂線の足を\(D\)とする。
底面の\(\triangle HBC\)は\(\angle BHC=90^{\circ}\)
の直角二等辺三角形だから、
\(HB=3\sqrt{2}\)
\(AB=\sqrt{AH^2+BH^2}\)
\(=\sqrt{(3\sqrt{3})^2+(3\sqrt{2})^2}\)
\(=\sqrt{27+18}=3\sqrt{5}\)
\(BD=3\)ゆえ
\(AD=\sqrt{AB^2-BD^2}\)
\(=\sqrt{(3\sqrt{5})^2-3^2}\)
\(=\sqrt{45-9}=6\)
よって、求める表面積は
\(6^2+6 \times 6 \times \frac{1}{2} \times 4\)
\(=36+72=108\)
(2) (答) \(108\) \((cm^2)\)
大問4

(2)解答例
(1)までに解っていること
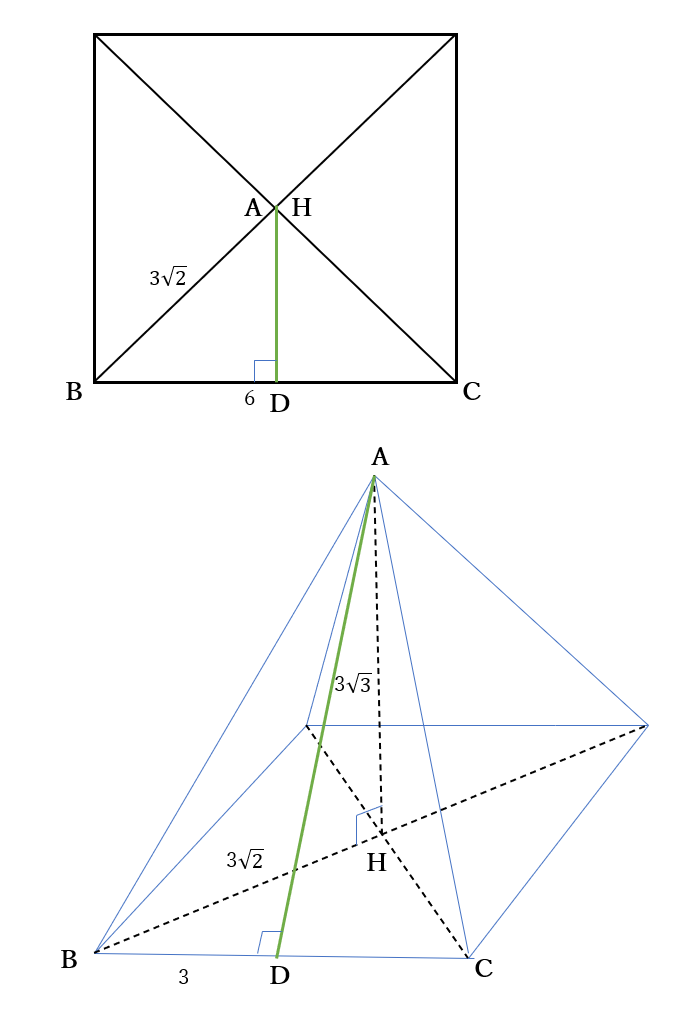
\(A(2,3),B(10,7),C(10,-5)\)
\(D(5,0),BC=12\)
右下の図のように、線分\(BC\)と\(x\)軸との交点を\(F\)、点\(A\)から\(x\)軸に下した垂線の足を\(G\)とする。
\(\triangle ABC\)の面積は
\(BC \times GF \times \frac{1}{2}\)
\(=12\times 8 \times \frac{1}{2}=48\)
\(\triangle DFC\)の面積は\(\frac{25}{2}\)なので、
\(\frac{25}{2} \lt 24\) より
求める直線は線分\(BF\)と交わる。
求める直線と線分\(BF\)との交点を
\(E(10,k)\) \((k \gt 0)\) とする。
\(\triangle DEC\)の面積は
\(EC \times 5 \times \frac{1}{2}\)
\(=\frac{5}{2}(k+5)\)
\(\iff \frac{5}{2}(k+5)=24\)
\(\iff k=\frac{23}{5}, \quad E(10,\frac{23}{5})\)
2点\(D\)、\(E\)を通る直線の方程式は
\(y=\frac{23}{25}x-\frac{23}{5}\)
これが求める直線の方程式である。
(2) (答) \(\large y=\frac{23}{25}x-\frac{23}{5}\)
大問5
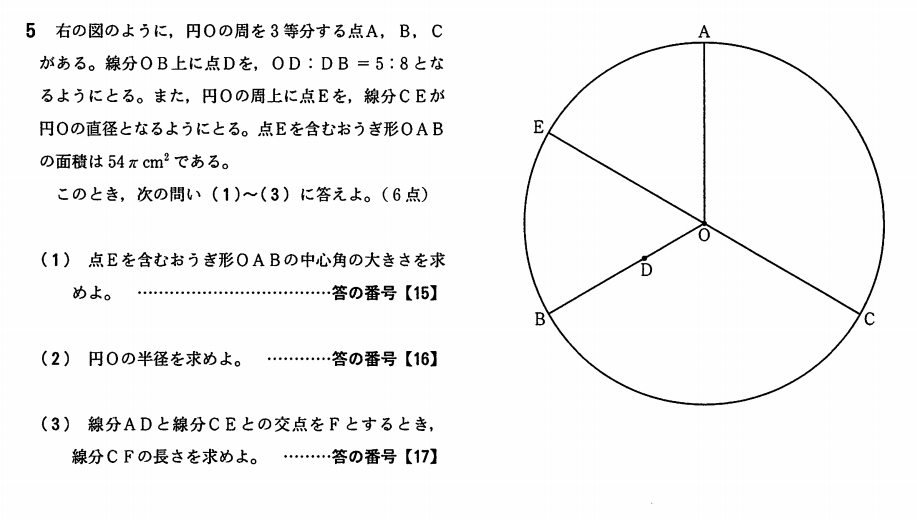
大問5(3)解答例
(2)までに解っていること
\(\angle AOB=120^{\circ}\) \((\angle AOE=\angle EOB=60^{\circ})\)
円\(O\)の半径は\(9\sqrt{2}\)
右下の図のように、線分\(AO\)の延長線上に、\(OF /\!/ GD\)となるように点\(G\)をとる。
\(\angle AOF=\angle AGD=60^{\circ}\)
\(\angle FOD=\angle ODG=60^{\circ}\)
\(\iff \triangle ODG\) は正三角形で
\(OD=GD=OG \ \cdots\) ①
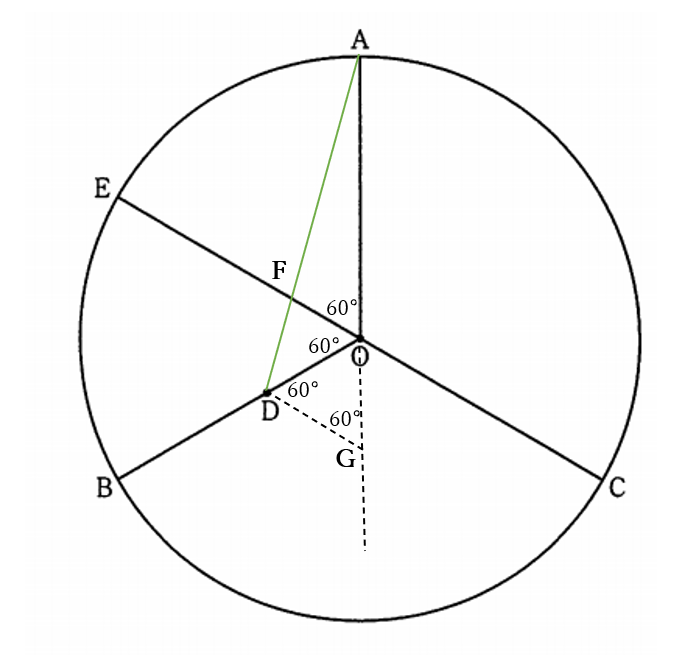
\(OD:DB=5:8\) より
\(OB:OD=13:5 \ \cdots\) ②
\(\iff OD=OB \times \frac{5}{13}\)
\(=9\sqrt{2} \times \frac{5}{13}=\frac{45}{13} \sqrt{2} \ \cdots\) ③
①②より\(AO:OG=13:5\)
\(\iff AG:AO=18:13\)
\(\triangle ADG \sim \triangle AFO\)だから
\(GD:OF=AG:AO=18:13\)
\(\iff OF=GD \times \frac{13}{18}\)
よって、①③より
\(OF=\frac{45}{13} \sqrt{2} \times \frac{13}{18}\)
\(=\frac{5}{2} \sqrt{2}\)
ゆえに
\(CF=OC+OF=9\sqrt{2}+\frac{5}{2} \sqrt{2}\)
\(=\frac{23}{2}\sqrt{2}\)
(3) (答) \(\large \frac{23}{2}\sqrt{2}\) \((cm)\)
大問6
(2)解答例
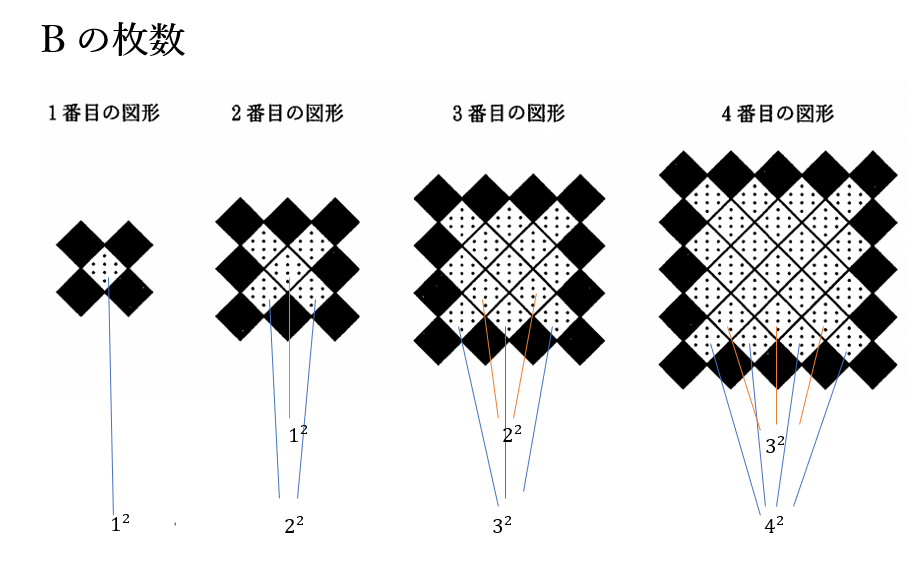
\(n\)を自然数とする
タイル\(B\)の枚数
1番目 \(1^2\)
2番目 \(2^2+1^2\)
3番目 \(3^2+2^2\)
4番目 \(4^2+3^2\)
・・・・・・・・・・・
\(n\)番目 \(n^2+(n-1)^2\)
9番目のタイル\(B\)の枚数は、
\(9^2+(9-1)^2=81+64\)
\(=145\)
(2) (答) 145枚
(3)解答例
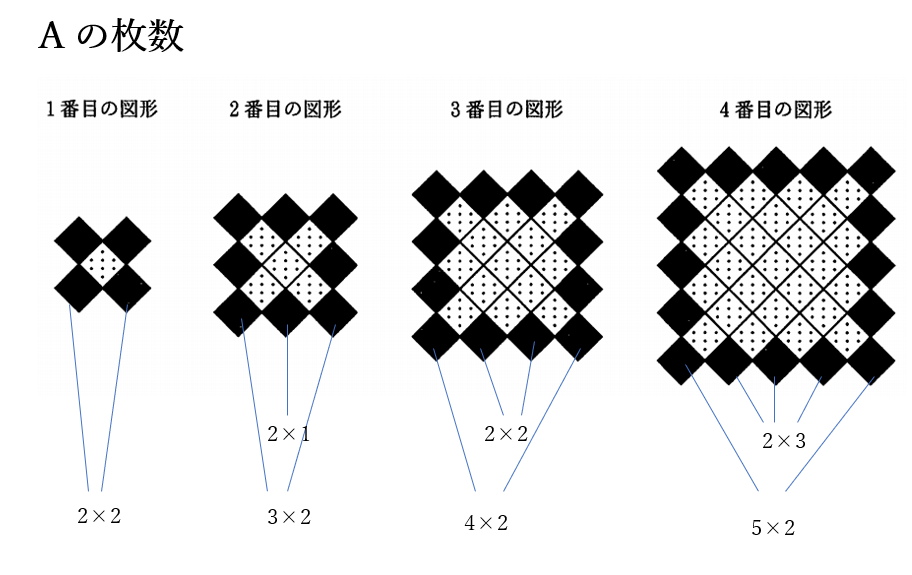
\(n\)を自然数とする
タイル\(A\)の枚数
1番目 \(2 \times 2+2 \times 0\)
2番目 \(3 \times 2+2 \times 1\)
3番目 \(4 \times 2+2 \times 2\)
4番目 \(5 \times 2+2 \times 3\)
・・・・・・・・・・・
\(n\)番目 \(2(n+1)+2(n-1)\)
\(=4n\)
\(n^2+(n-1)^2-4n=1009\)
\( \iff n^2-3n-504=0\)
\(\iff (n-24)(n+21)=0\)
\(\iff n=24\)
(3) (答) 24番目
