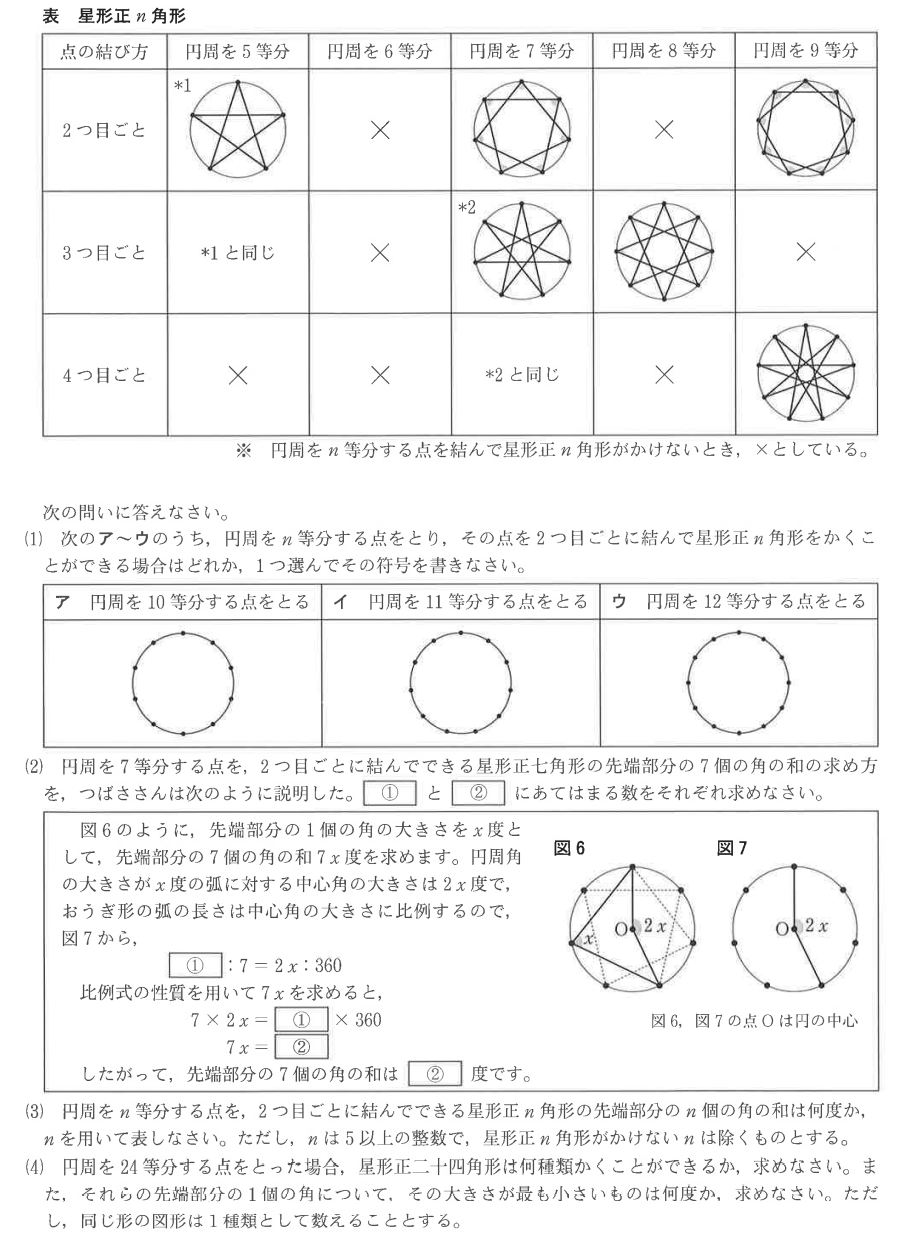
なかなか手ごわい問題が多い。とくに、最後の大問6の(4)は思考時間をたっぷりと必要とする。
大問3
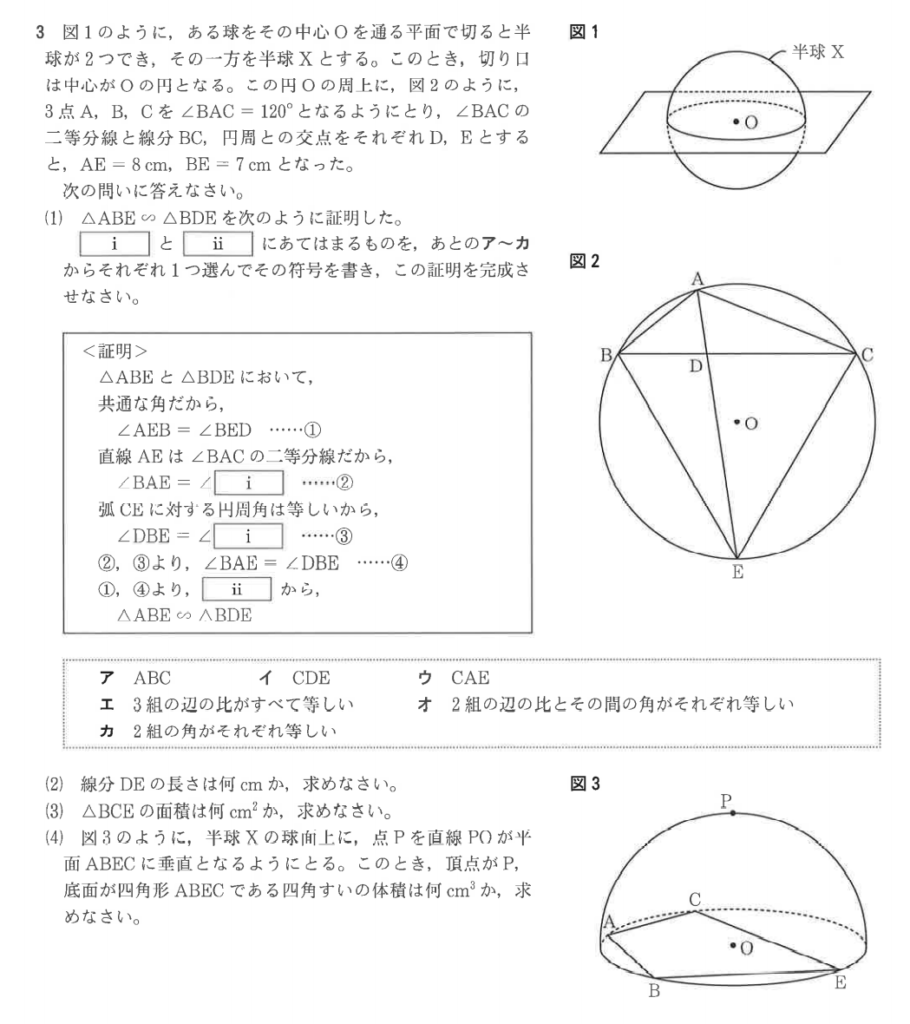
(2)解答例
(1)より\(\triangle ABE \sim \triangle BDE\)
\(AE=8cm, \ BE=7cm\) ゆえ
\(AE:BE=8:7\)
\(\iff BE:DE=8:7\)
\(\iff DE=BE\times \frac{7}{8}\)
\(=7\times \frac{7}{8}=\frac{49}{8}\)
(2) (答) \(\large \frac{49}{8}\) \((cm)\)
(3)解答例
右下の図のように
\(E\)から線分\(BC\)に下した垂線の足を\(H\)とする。
題意より
\(\angle BAE=\angle CAE=60^{\circ}\)
\(\iff \angle EBC=\angle ECB=60^{\circ}\)
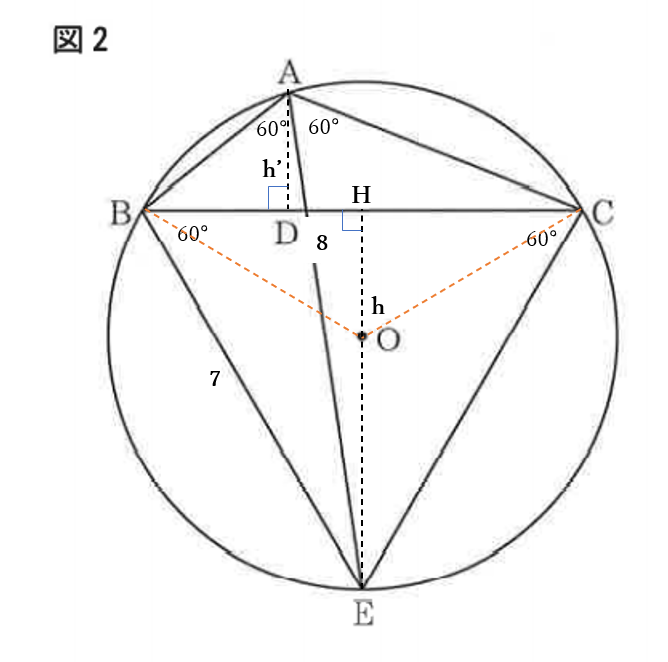
よって、\(\triangle BCE\) は、正三角形
\(EB:EH=2:\sqrt{3}\)
\(\iff EH=\large \frac{7\sqrt{3}}{2}\)
\(\iff \triangle BCE=BC\cdot EH\cdot \frac{1}{2}\)
\(=7 \cdot \large \frac{7\sqrt{3}}{2} \cdot \frac{1}{2}=\frac{49\sqrt{3}}{4}\)
(3) (答) \(\large \frac{49\sqrt{3}}{4}\) \((cm^2)\)
(4)解答例
四角形\(ABEC\) の面積をもとめる
右の図のように\(A\)から線分\(BC\)に下した垂線の長さを\(h’\)、\(EH=h\)とする
(1)(2)より
\(AD=AE-DE=8-\frac{49}{8}\)
\(=\frac{15}{8}\)
\(h’:h=AD:DE\)
\(=\frac{15}{8}:\frac{49}{8}=15:49\)
\(\iff h’=\frac{15}{49}h=\large \frac{15}{49}\frac{7\sqrt{3}}{2}\)
\(=\large \frac{15\sqrt{3}}{14}\)
\(\triangle ABC\)の面積は
\(BC\cdot h’\times \frac{1}{2}=7 \large \frac{15\sqrt{3}}{14}\frac{1}{2}\)
\(=\large \frac{15\sqrt{3}}{4}\)
(3)より 四角形\(ABEC\) の面積は
\(\triangle ABC+\triangle BCE\)
\(=\large \frac{15\sqrt{3}}{4}+\frac{49\sqrt{3}}{4}\)
\(=\large \frac{64\sqrt{3}}{4}=16\sqrt{3}\cdots\)①
・・・・・・・・・・・・・・・・・・・・
《①の別解》
\(h:h’=DE:AD\)より
\(\frac{h+h’}{h}=\frac{AE}{DE}\)
四角形\(ABCE=\triangle BCE \times \frac{AE}{DE}\)
\(=\large \frac{49\sqrt{3}}{4} \times \frac{8}{\frac{49}{8}}\)
\(=16\sqrt{3}\)
・・・・・・・・・・・・・・・・・・・・・
\(PO\)は四角錐\(P-ABCE\)の高さであり、半球の半径でもあり
\(PO=OB=OE=OC\)
また、\(\triangle BEC\) は正三角形であり、
\(\triangle OBE \equiv \triangle OEC \equiv \triangle OCB\) だから、
\(\triangle OBH\) は \(\angle OBH=30^{\circ}\) の直角三角形
よって、\(\large OB=BH\times \frac{2}{\sqrt{3}}\)
\(\large =\frac{7}{2}\frac{2}{\sqrt{3}}\)
\(\large =\frac{7}{\sqrt{3}}\)
ゆえに、求める四角錐の体積は①より
\(\large 16\sqrt{3} \times \frac{7}{\sqrt{3}} \times \frac{1}{3}\)
\(=\frac{112}{3}\)
(4) (答) \(\large \frac{112}{3}\) \((cm^3)\)
大問4
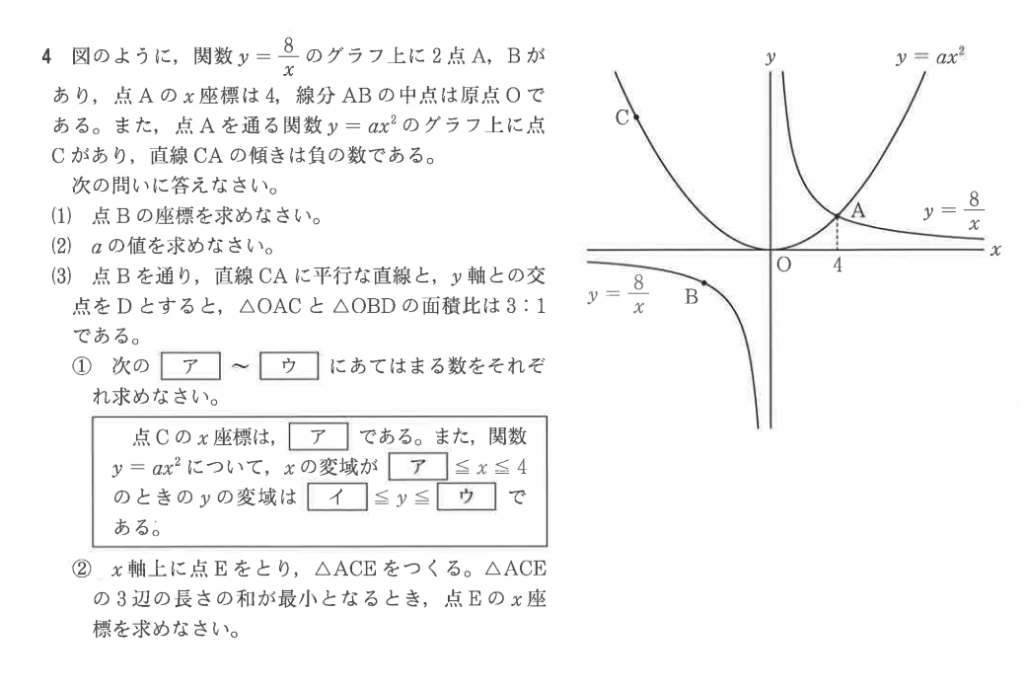
(3)解答例
①
(1)(2)より
2次関数 \(y=\frac{1}{8}x^2\)
\(A(4,2), \ B(-4,-2)\)
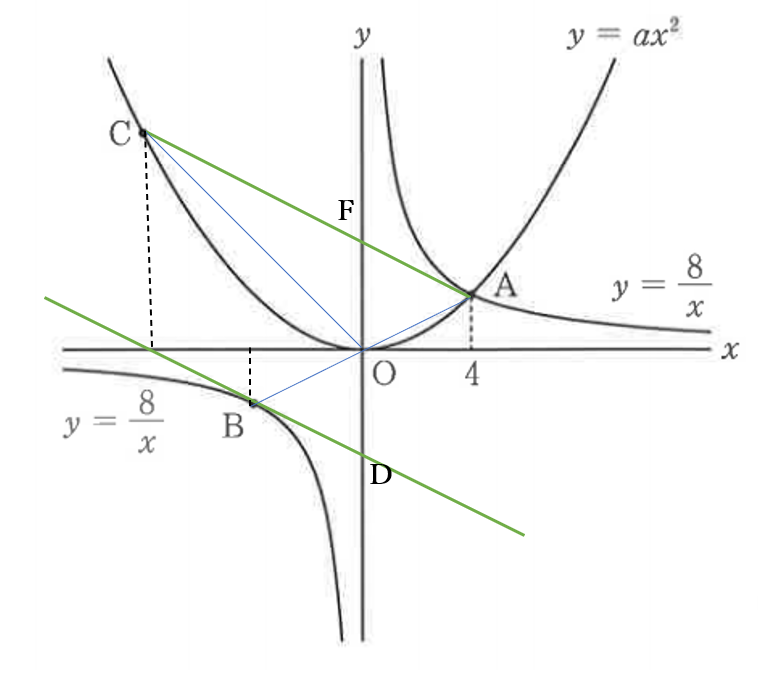
右下の図のように、直線\(CA\)と\(y\)軸との交点を\(F\)とする
\(AF // BD\)
\( \iff OF=OD\cdots\)①
\(\iff \triangle OAF=\triangle OBD\)
よって
\(\triangle OAC:\triangle OBD=3:1\) より
\(\iff \triangle OFC:\triangle OBD=2:1\)
\(C\)の\(x\)座標を\(k\)とおくと
①より\(k:-4=2:1\)
\(k=-8\)
\(x=-8, \ C(-8,8)\)
ゆえに \(y=\frac{1}{8}x^2\)について、
\(-8 \leq x \leq 4\) のとき \(0 \leq y \leq 8\)
(3)① (答) ア \(-8\) 、 イ \(0\) 、 ウ \(8\)
②
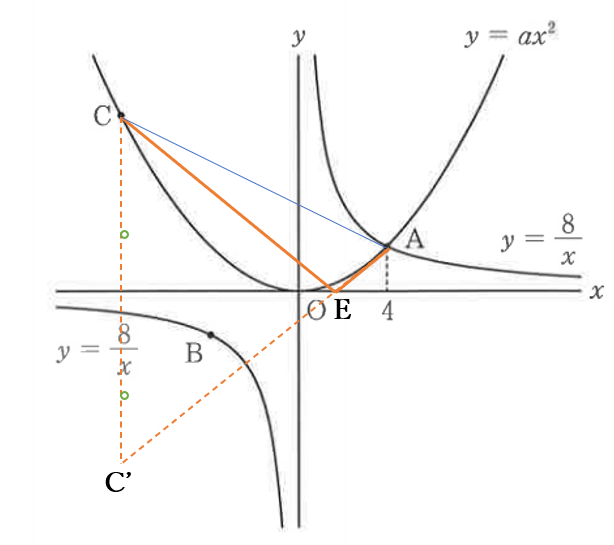
\(\triangle ACE\)の線分\(AC\)は一定であるから、
\(AE+EC\)が最小となる点\(E\)を求めればよい。
右下の図のように、
\(x\)軸に関して\(C\)と対称な点を\(C’\)とする
直線\(AC’\)と\(x\)軸との交点を\(E\)とおくと
\(EC=EC’\)だから
このときの点\(E\)が求める点である。
\(C'(8,-8)\)だから直線\(AC\)の方程式は
\(y=\frac{5}{6}x-\frac{4}{3}\)
\(y=0\iff x=\frac{8}{5}\)
求める点\(E\)の\(x\)座標は \(\frac{8}{5}\)
(3)② (答) \(\large \frac{8}{5}\)
大問5

(3)解答例
落ち着いて漏れなく数える。
\(\sqrt{0},\sqrt{1}\) を忘れないようにしよう
①
表1枚
\(\sqrt{1}, \ \sqrt{4}, \ \sqrt{9}\)
の3通り
表2枚
\((1,4)\Rightarrow \sqrt{4},\quad (1,9)\Rightarrow \sqrt{9}\)
\((2,8)\Rightarrow \sqrt{16},\quad (4,9)\Rightarrow \sqrt{36}\)
の4通り
(3)① (答) 7 (通り)
②
表が0枚
\(\sqrt{0}\) の1通り
①より表が1枚または2枚のとき 7通り
表が3枚
\((1,2,8)\Rightarrow \sqrt{16}, \quad (1,4,9)\Rightarrow \sqrt{36}\)
\((2,4,8)\Rightarrow \sqrt{64}, \quad (2,8,9)\Rightarrow \sqrt{144}\)
の4通り
表が4枚
\((1,2,4,8)\Rightarrow \sqrt{64}, \quad (1,2,8,9)\Rightarrow \sqrt{144}\)
\((2,4,8,9)\Rightarrow \sqrt{576}\)
の3通り
表が5枚
\((1,2,4,8,9)\Rightarrow \sqrt{576}\) の1通り
合わせて16通りだから求める確率は
\(\large \frac{16}{2^6}=\frac{1}{4}\)
(3)② (答) \(\large \frac{1}{4}\)
大問6

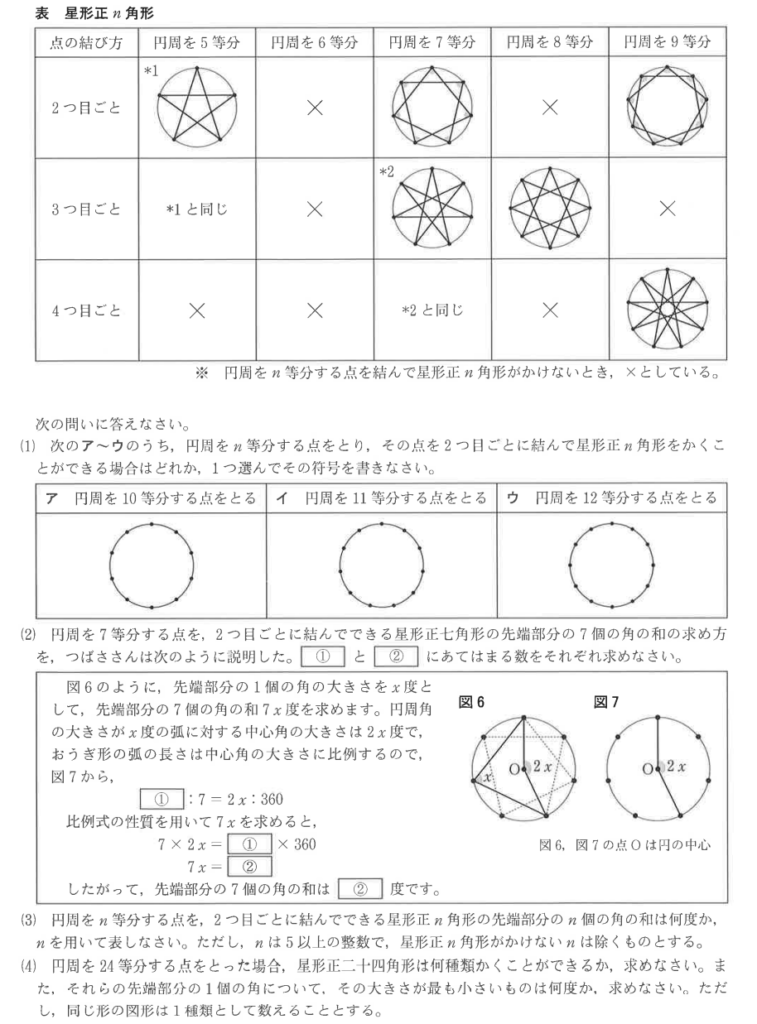
(3)解答例
\((n-4):n=2x:360^{\circ}\)
\(\iff n\cdot 2x=(n-4)360^{\circ}\)
\(\iff nx=180^{\circ}(n-4)\)
(3) (答) \(180^{\circ}(n-4)\)
(4)解答例
24等分する点を\(k\)個目ごとに結んで星形正24角形が作れるのは、\(k\)と\(24\)が互いに素であるときである。ただし、\(2 \leq k \leq 12\) である。\(k \geq 13\) は逆回りで同じことになる。\(k=1\)は星形にならないから除外する。
\(k\)と24が互いに素ならば、\(k\)と24の最小公倍数が\(k \times 24\)となり、すべての点を直線で結んでからスタートの点に戻り、星形正24角形が作れる。
〔解説〕
【2つの整数 \(a\) と \(b\) が互いに素】
\(a\) と \(b\) の公約数が1のみ(1以外に公約数がない)
たとえば、\(k=2,3,4,6,8,12\) は、24の約数なので、1週目でスタートの点に戻ってしまい、24角形は描けない。
残りの候補は、\(k=5,7,9,10,11\) である。
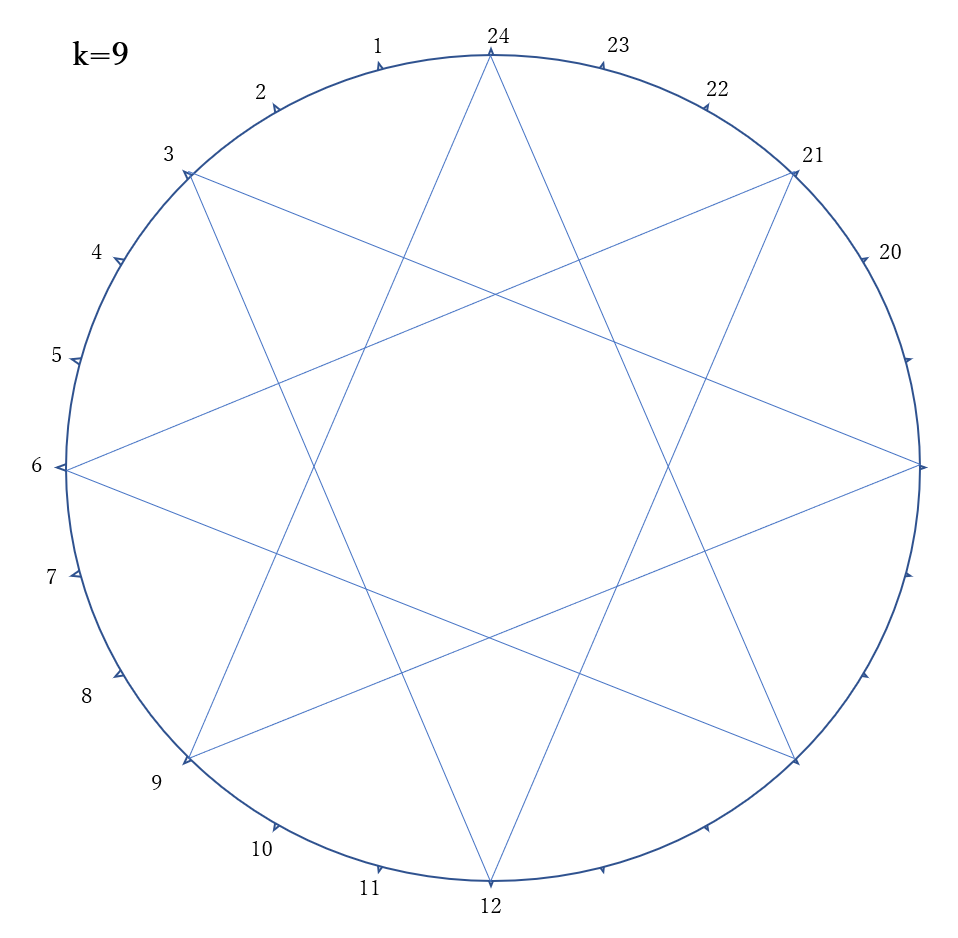
《\(k=9\)のとき》
9と24は互いに素ではない。9と24の最小公倍数は\(9 \times 8=72\)だから、8本目の直線を引いたときにスタートの点に戻ってしまい、星形正8角形になる。
右の図
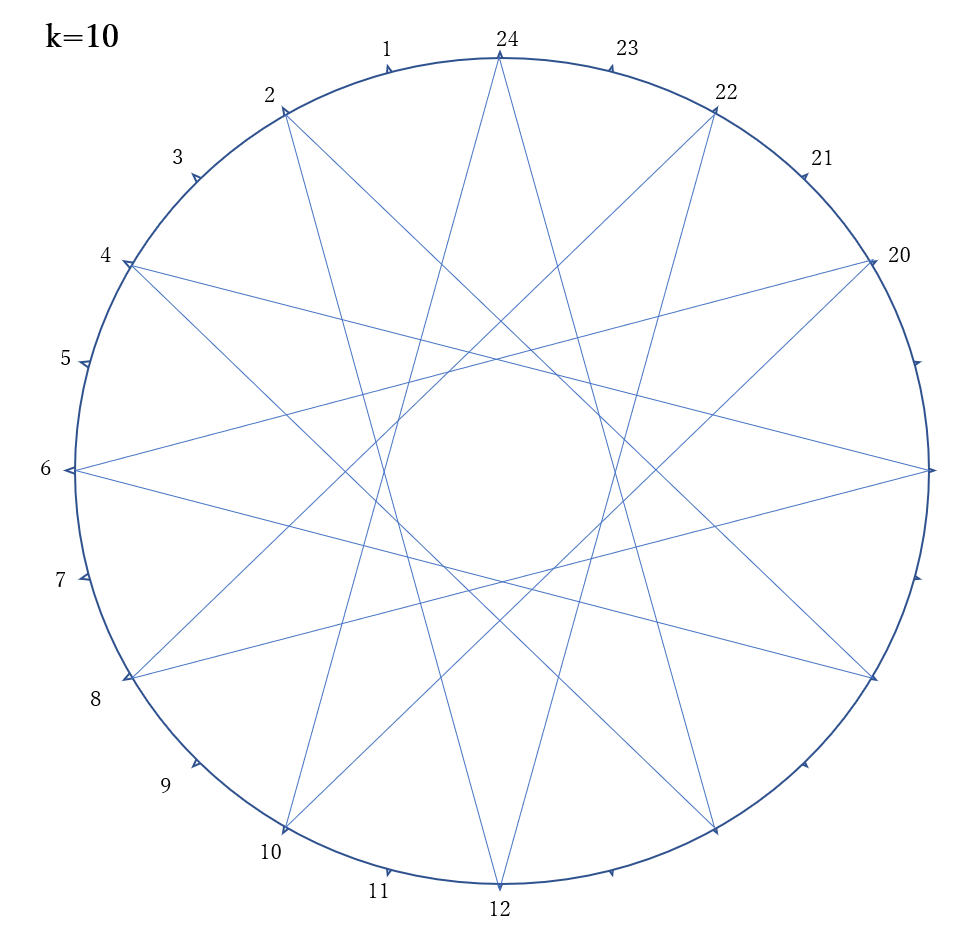
《\(k=10\)のとき》
10と24は互いに素ではない。10と24の最小公倍数は\(10 \times 12=120\)だから、12本目の直線を引いたときにスタートの点に戻ってしまい、星形正12角形になる。
右の図
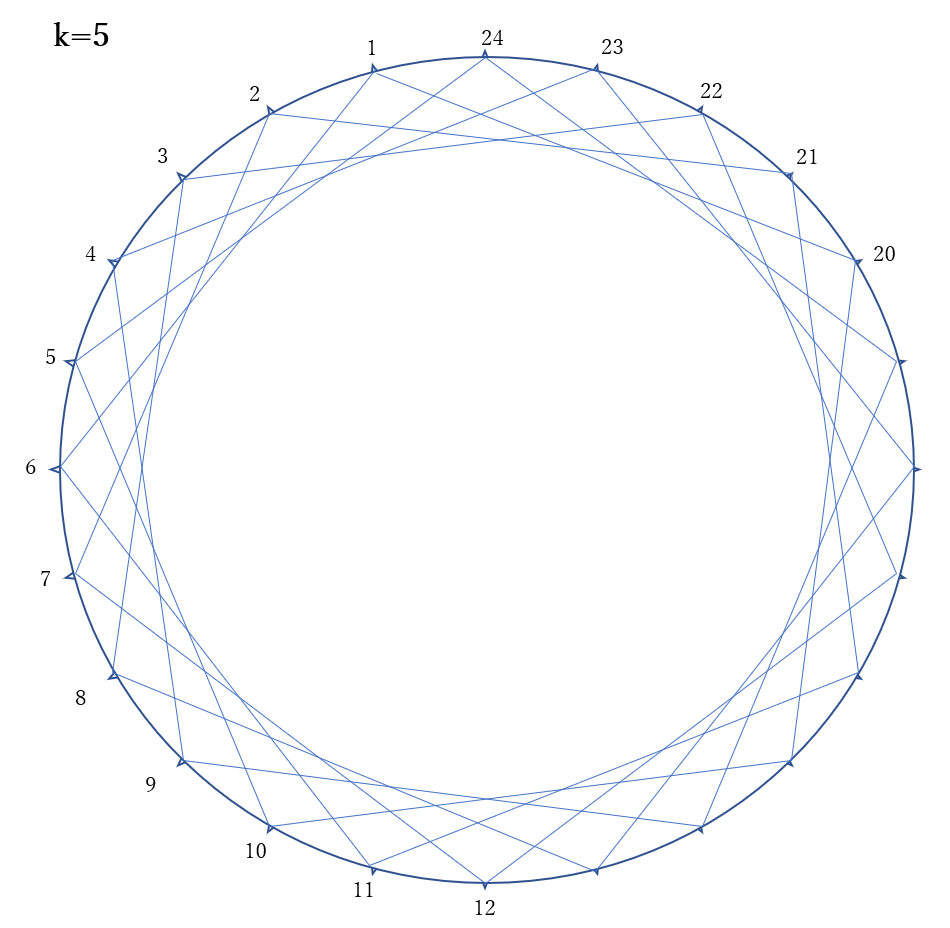
したがって、星形正24角形を作れるのは、\(k\)と24が互いに素のとき、つまり、\(k=5,7,11\)のときである。したがって、3種類かくことができる。
右の図
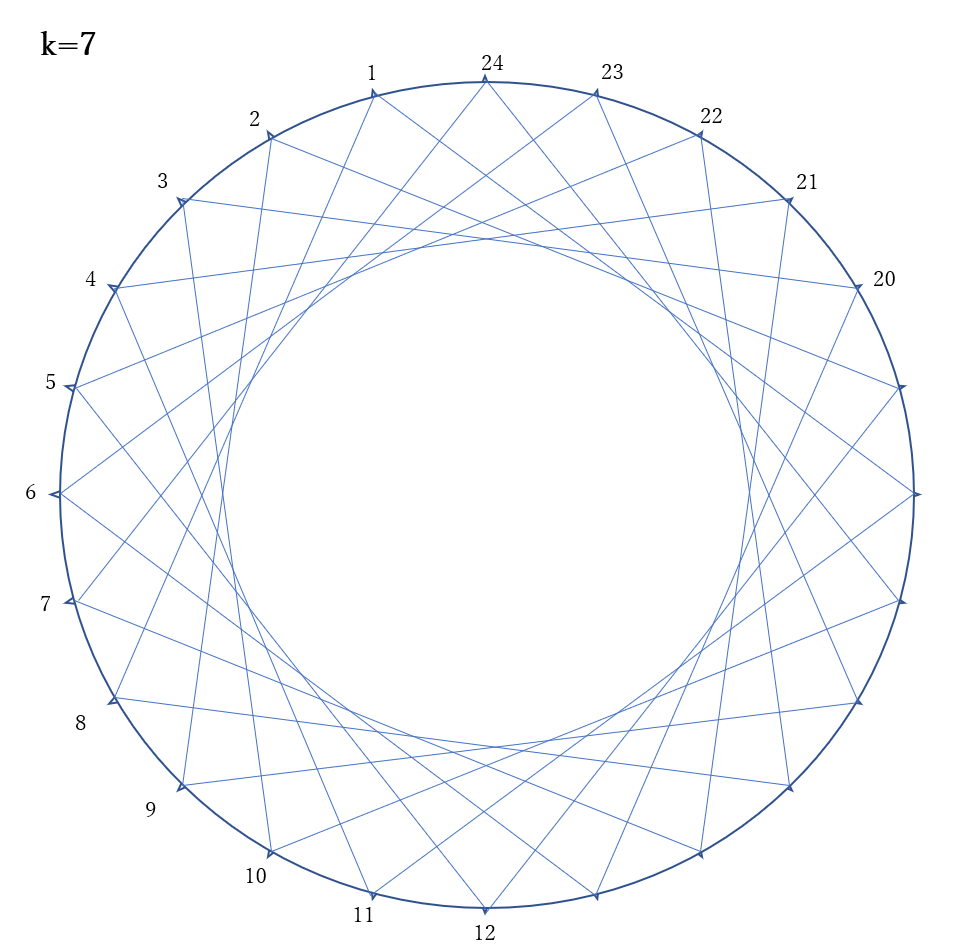
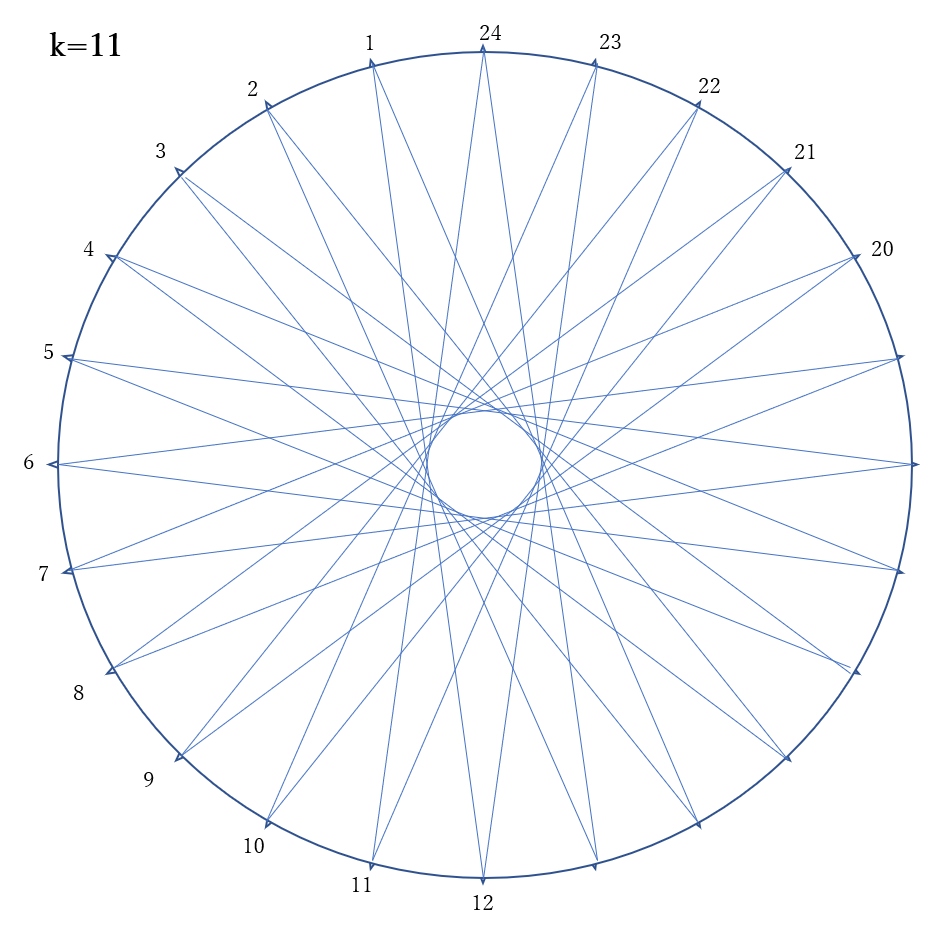
先端部分の角が一番小さくなるのは、11個目ごとに結んだ場合である。11個目ごとに結んでできる星形正24角形の角の大きさは、24等分された円周の2個分の円周角と等しい。よって、その中心角は
\(360^{\circ}\times \frac{2}{24}=360^{\circ}\times \frac{1}{12}=30^{\circ}\)
ゆえに円周角は\(15^{\circ}\)
(4) (答) 3種類 、 15 (度)
追伸
ほとんどの公立中学校では、「互いに素」の意味を教えていないと思う。「約数」とか「最小公倍数」を使って解くことになるだろうが、難解で時間がかかる。(3)まで解ければ成功。