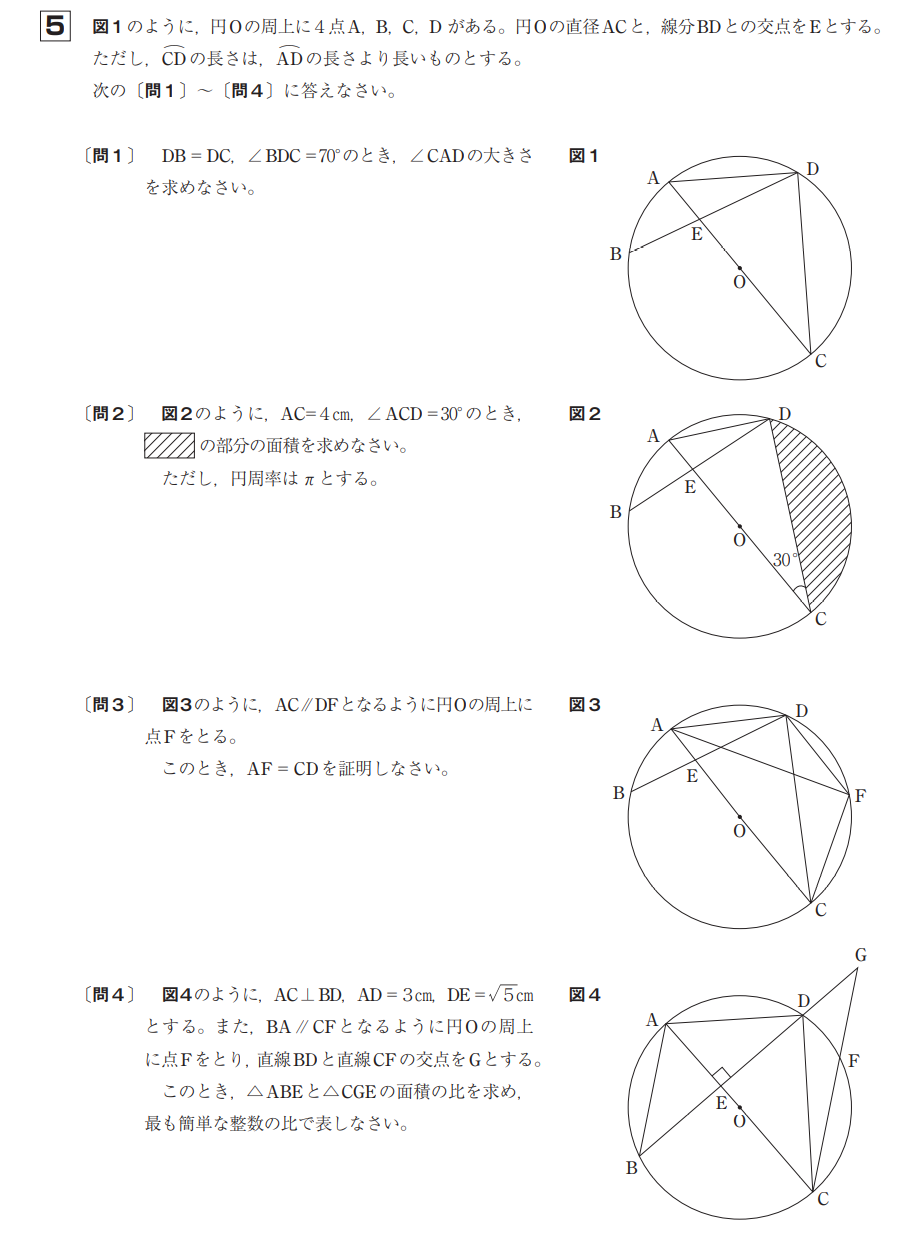
大問3⃣の規則性の問題は、ヒントが随所に書かれていて、解きやすくなっている。問題を落ち着いて読んで理解すれば、比較的楽に答えにたどり着く。大問4⃣〔問3〕の動点の問題は、場合分けして考える。大問5⃣の面積問題は、三角形の相似比を使う。
大問4⃣

〔問3〕 解答例
\(0 \leq x \lt 2\)のとき
\(PO \lt PQ\)
\(4 \leq x \lt 6\)のとき
\(PO \gt PQ\)
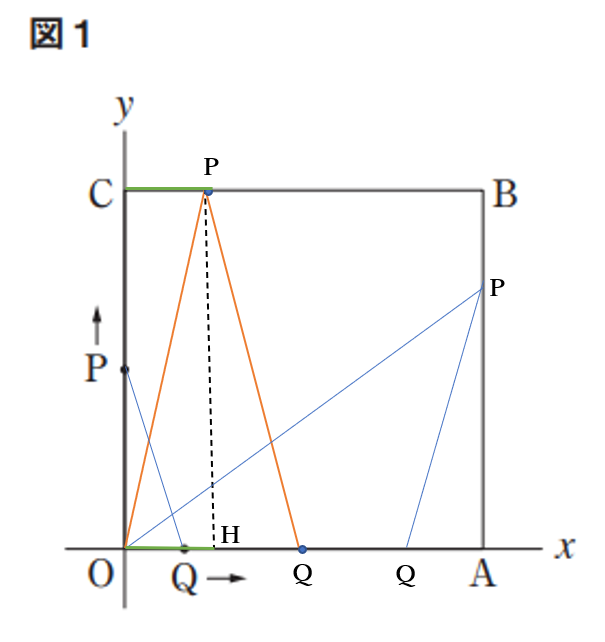
\(2 \leq x \lt 4\)のとき
\(PO=PQ\)になるときがあり
そのとき\(\triangle POQ\)は二等辺三角形
右の図のように
\(P\)から線分\(OQ\)に下した垂線の足を\(H\)とすると
\(CP=OH\)
\(CP=3x-6,OH=\frac{1}{2}x\)
\(\iff 3x-6=\frac{1}{2}x\)
\(\iff x=\frac{12}{5}\)
〔問3〕 (答) \(\large \frac{12}{5}\) (秒後)
〔問4〕解答例
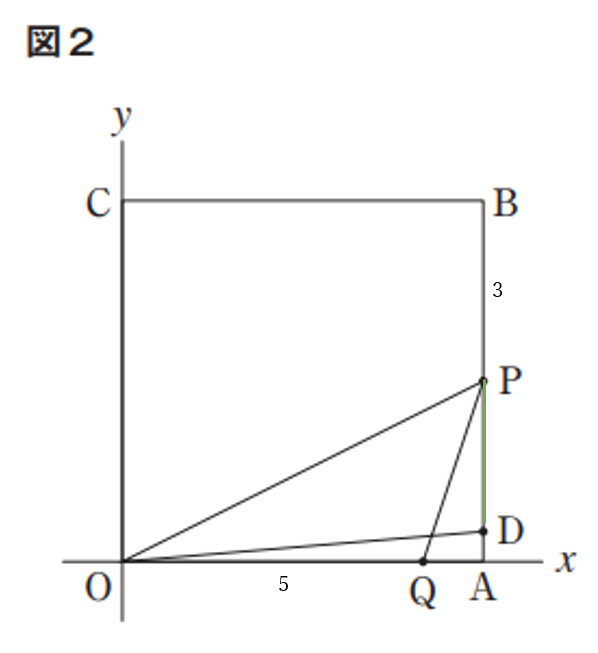
出発してから5秒後のとき
\(BP=PA=3, \ OQ=5\)
よって
\(\triangle OPQ=\frac{15}{2},\ \triangle OPD=3PD\)
\(\triangle OPQ=\triangle OPD\)
\( \iff 3PD=\frac{15}{2}\)
\(\iff PD=\frac{5}{2}\)
\(\iff AD=\frac{1}{2}\)
\(\iff D(6,\frac{1}{2})\)
〔問4〕 (答) \(\large D(6, \ \frac{1}{2})\)
問5⃣
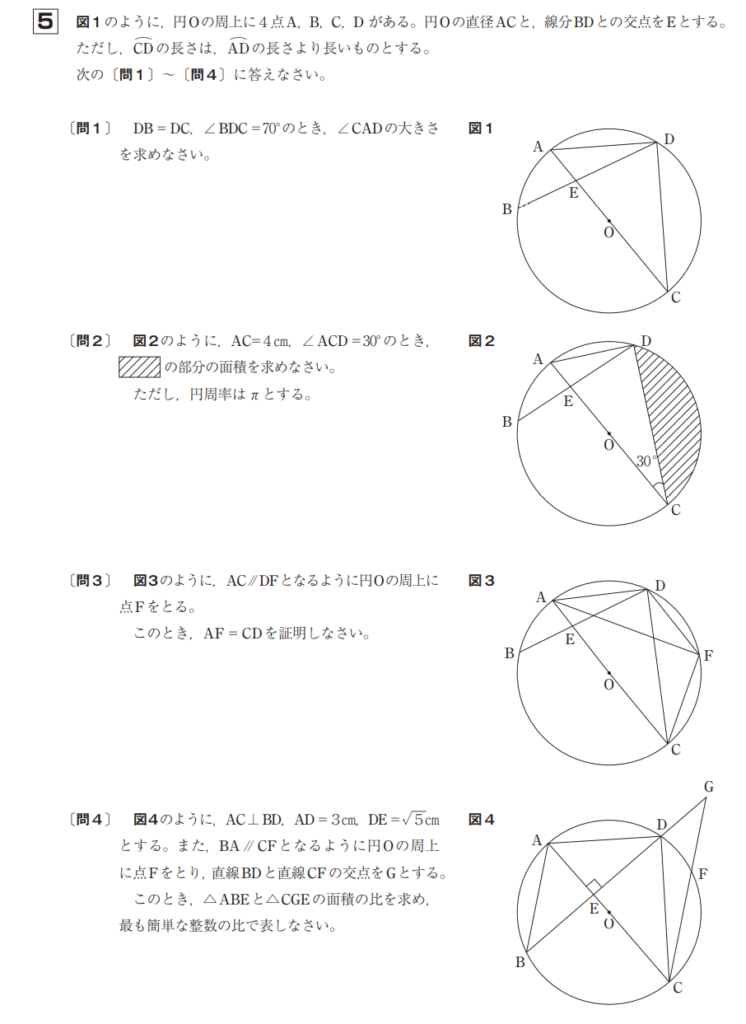
〔問4〕解答例
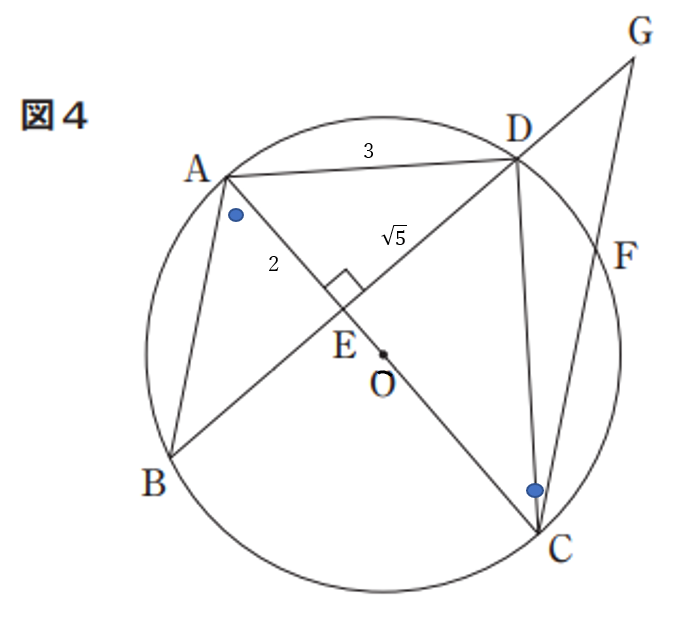
\(AE=\sqrt{3^2-(\sqrt{5})^2}=2\)
また
\(\triangle ADE \sim \triangle DCE\) だから
\(CE:ED=ED:EA\)
\(\iff CE=\frac{\sqrt{5}}{2}\times \sqrt{5}\)
\(=\frac{5}{2}\)
\(\triangle ABE\)と\(\triangle GCE\)において
\(AB//CF\) より
\(\angle BAE=\angle GCE\) (錯角)
よって
\(\triangle ABE \sim \triangle GCE\)
\(AE:CE=2:\frac{5}{2}\)
\(\triangle ABE:\triangle CGE=2^2:(\frac{5}{2})^2\)
\(=16:25\)
〔問4〕 (答) \(\triangle ABE:\triangle CGE \ = \ 16:25\)