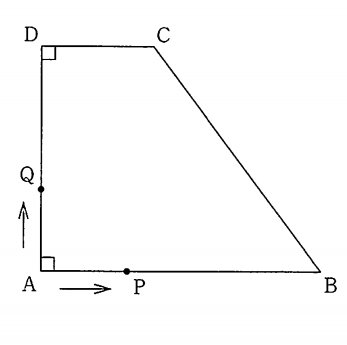
率直に言って、問題数が多い。大問1から大問5まで、制限時間50分ですべてに解答することはかなり難しいと思う。大問1を小問(1)から(10)まで解答するのに15分は欲しい。残りの大問4つを35分で...。考える問題もいくつかあるので、時間との戦いになる。
最後の大問5の(2)(3)は、焦っていたら解答は難しい。大問5の(2)(3)を考察してみよう。

大問5(2)解答例
\(\triangle APQ ,\quad \triangle AQC\) の面積を表す式は
\(0 \lt x \leq 4,\quad 4 \lt x \leq 5\)
\( 5 \lt x \leq 6,\quad 6 \lt x \leq 11\)
で、異なるから、これら4通りに分けて考える。
\(\triangle APQ\) の面積を\(y\)
\(\triangle AQC\) の面積を\(y’\) とおく
① \(0 \lt x \leq 4\) のとき
\(y=\frac{1}{2}x^2,\quad y’=x\)
\(y:y’=3:1 \iff \frac{1}{2}x^2=3x\)
\( \iff \frac{1}{2}x(x-6)=0\)
\(\iff x=0,6\) これは不適
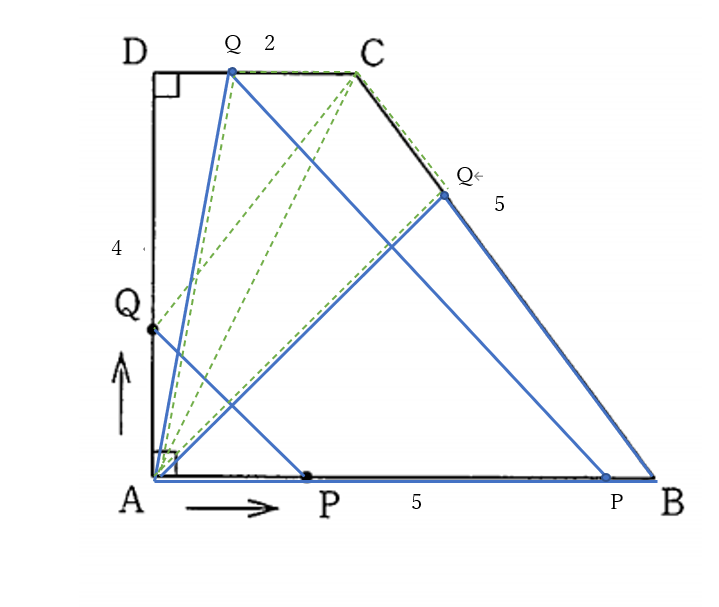
② \(4 \lt x \leq 5\) のとき
\(y=2x,\quad y’=2(6-x)\)
\(y:y’=3:1 \iff 2x=6(6-x)\)
\( \iff 2x=36-6x\)
\( \iff 8x=36\)
\(\iff x=\frac{9}{2}\) これは適する。
③ \(5 \lt x \leq 6\) のとき
点\(P\) は 点\(B\) にあるから
\(y=10,\quad y’=2(6-x)\)
\(y:y’=3:1 \iff y=3y’\)
\( \iff 10=6(6-x)\)
\(\iff x=\frac{13}{3}\) これは不適
④ \(6 \lt x \leq 11\) のとき
点\(P\) は 点\(B\) にあるから
\(y:y’=3:1 \iff QP:CQ=3:1\)
\( \iff CQ= \frac{1}{4} \times CB= \frac{5}{4} \)
\( \iff x=4+2+\frac{5}{4}=\frac{29}{4}\)
これは適する
(答) \(\displaystyle \frac{9}{2}, \quad \displaystyle \frac{29}{4}\)
大問5(3)解答例
台形\(ABCD\)の面積は、\( \frac{1}{2} \times (2+5) \times 4=14\)だから
台形\(ABCD\)の面積の半分は7
\( \triangle APQ \)の面積\(y\)を表す\(x\)の式は
点\(Q\)が、辺\(AD\)上、辺\(DC\)上、辺\(CB\)上にいるときで変わるから
次の3つの場合に分けて考える
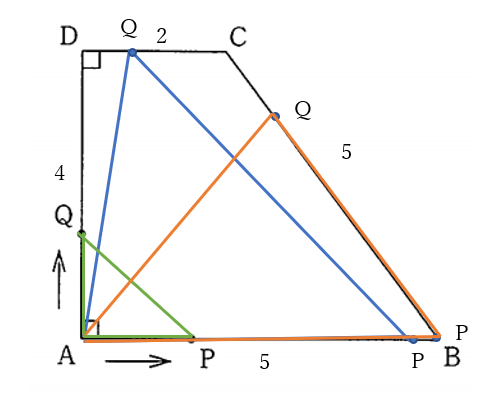
①点\(Q\)が辺\(AD\)上にあるとき、すなわち、
\(0 \lt x \leq 4\) のとき
②点\(Q\)が辺\(DC\)上にあるとき、すなわち、\(4 \lt x \leq 6\) のとき
③点\(Q\)が辺\(CB\)上にあるとき、すなわち、
\(6 \lt x \leq 11\) のとき
① \(0 \lt x \leq 4\)のとき $$ y= \frac{1}{2} x^2=7 \iff x=\sqrt{14} $$ ② \(4 \lt x \leq 6\)のとき
\(\triangle APQ\)の面積は明らかに7より大きくなるから不適
③ \(6 \lt x \leq 11\)のとき(点\(P\)は点\(B\)に止まっている)
\( \triangle CAB\)の面積は10であるから
\(\triangle APQ\)の面積が7\(\iff CQ:QB=3:7\)
\(\iff CQ=CB \times \frac{3}{10}=5 \times \frac{3}{10}=\frac{3}{2}\)
\(\iff x=4+2+\frac{3}{2}=\frac{15}{2}\)
(答)\(x=\sqrt{14},\) \(\displaystyle \frac{15}{2}\)