問題42
長方形\(ABCD\)があります。
\(E,F\)はそれぞれ辺\(BC, \ CD \ \)上の点で、
\(EC=2BE, \ FC=3DF \ \)です。
また、\(G \ \)は線分\(AE \ \)と線分\(BF \ \)との交点です。
\(AB=4 \ cm, \ BC=6 \ cm\)のとき、線分\(AG \ \)の長さは、線分\(GE \ \)の長さの何倍か、求めなさい。
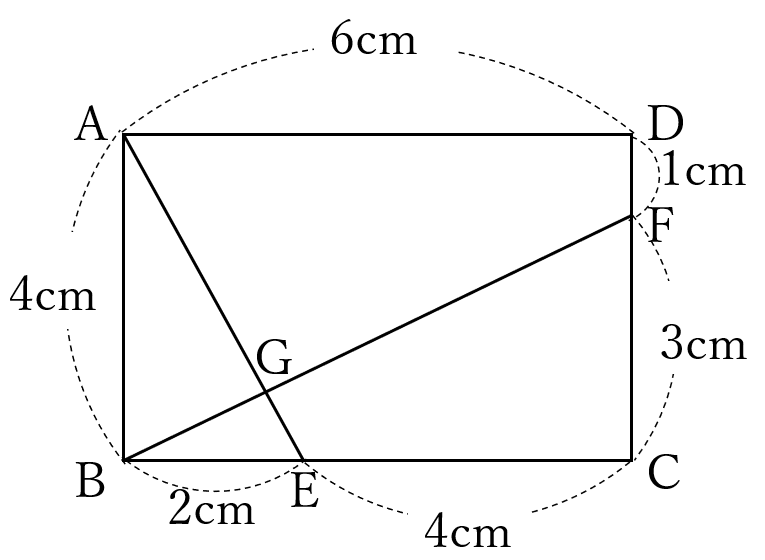
暗算で求めやすいように、図に長さを記入しておきました。ちょっとした工夫で、整数だけで計算できます。
頭の中でイメージしましょう。
解答
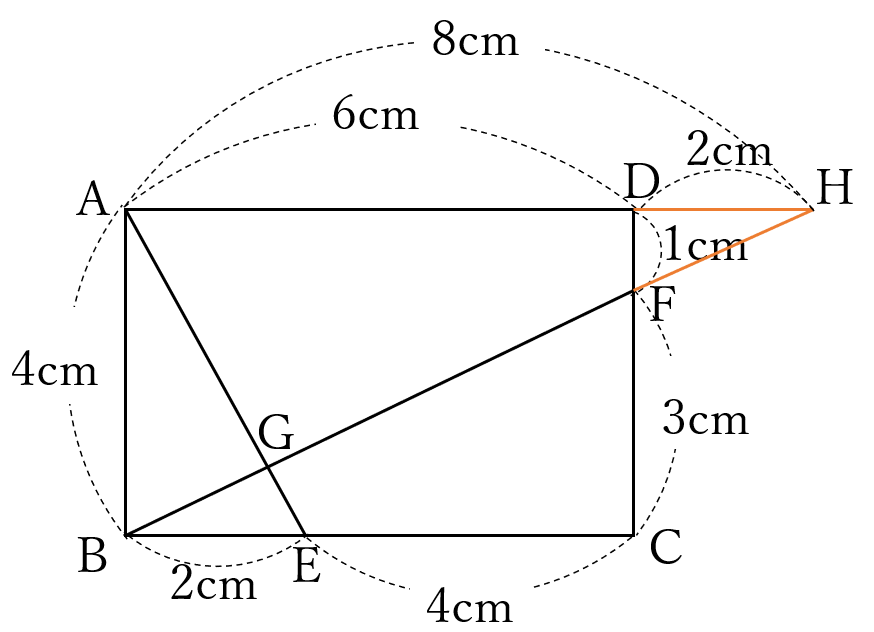
(答) \(\Large 4 \ \)倍
右の図のように、直線\(BF \ \)の延長線と辺\(AD \ \)の延長線との交点を\(H \ \)とします。
\(\triangle ABH \ \)∽\( \ \triangle CFB\)だから、\(AH:AB=CB:CF=2:1\)
よって、\(AH=2AB=8\)
\(\triangle GAH \ \)∽\( \ \triangle GEB\)なので、\(GA:GE=AH:EB=8:2=4:1\)
よって、\(AG=4GE\)
問題34
下の図は、線分\(AB\)を直径とする円\(O\)を底面とし、線分\(AC\)を母線とする円錐です。
\(AC=9 \ cm, \ AB=6 \ cm \ \)のとき
この円錐の表面積を求めなさい。
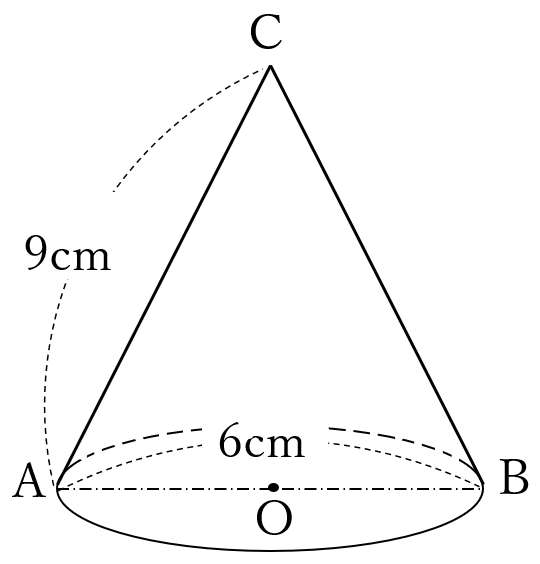
公式を利用すると、暗算で答が出ます。
解答
(答) \(\Large 36 \pi\) \((cm^2)\)
側面の扇形の面積は
\(\pi \times (母線) \times (底面の半径) \)
\(=\pi \times 9 \times 3\)
\(=27\pi\)
底面の面積は
\(\pi \times 3^2=9\pi\)
よって、求める表面積は
\(27\pi + 9\pi\)\(\large =36\pi\)
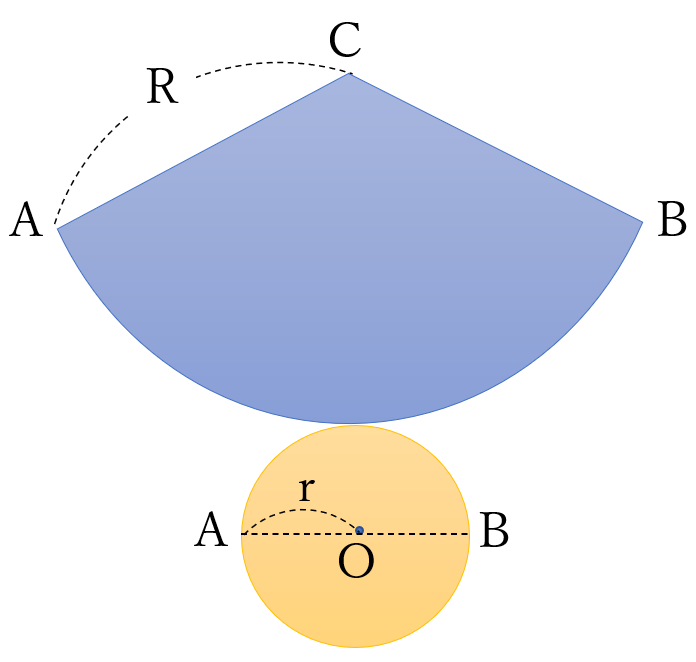
(公式)
側面の扇形の面積
\(=\pi R^2 \times \frac{2\pi r}{2\pi R}=\pi Rr \Leftarrow\)覚えよう!
底面の円の面積
\(=\pi r^2\)
よって、表面積は
\(\pi Rr + \pi r^2=\pi r(R+ r)\)
側面積だけを問われることがあるので
\(\pi Rr \ \)を覚えておこう。
問題35
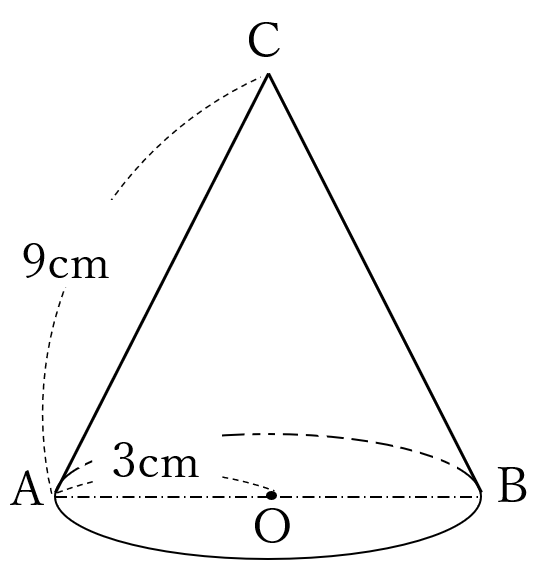
線分\(AB\)を直径とする円\(O\)を底面とし、線分\(AC\)を母線とする円錐です。
\(AC=6 \ cm, \ AB=6 \ cm \ \)のとき
この円錐の体積を>求めなさい。
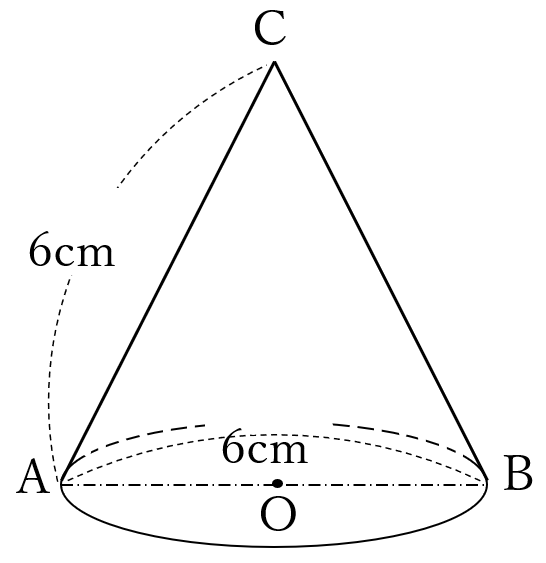
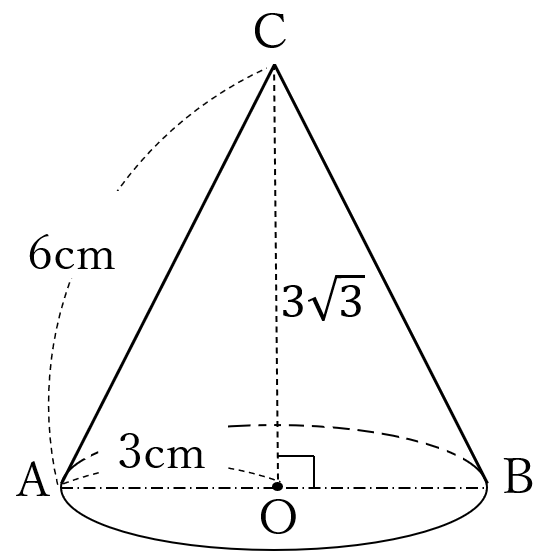
解答
(答)\(\Large 9\sqrt{3} \pi\) \((cm^3)\)
円錐や角錐の体積問題では、高さが√になってしまい、計算しずらくなります。この問題では高さが√になってもなんとか暗算で計算できます。
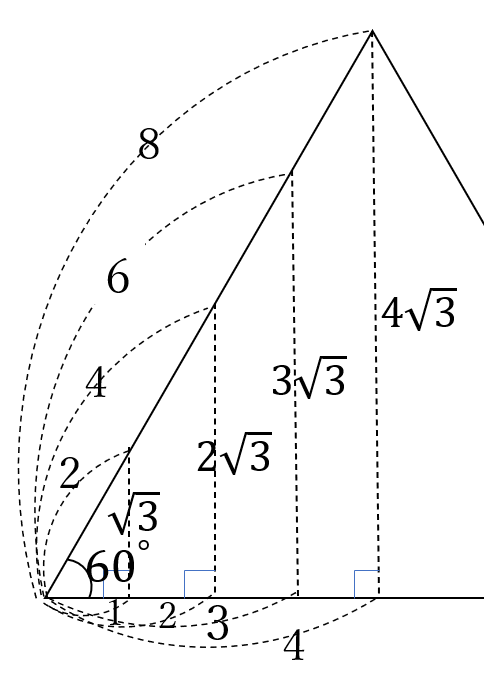
この円錐の高さは\(CO\)です。
\(\triangle CAO \ \)は、\(2:1:\sqrt{3}\)
の直角三角形なので
\(CO=3\sqrt{3} \ \)(右図)
\(V=\frac{1}{3} \pi r^2 h\)
\(=\frac{1}{3} \pi \times 3^2 \times 3\sqrt{3}\)
\(=9\sqrt{3} \ \pi\)
問題41
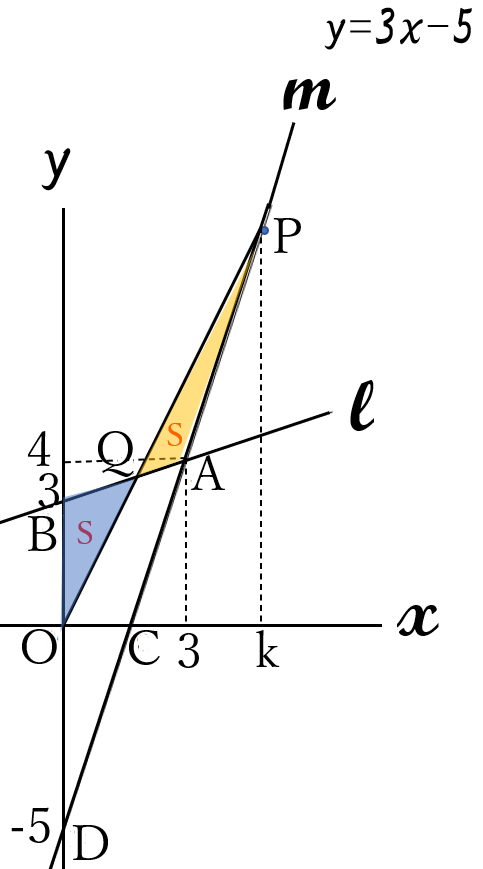
右の図のように、
2点\(A(3,4)\)、\(B(0,3)\)
があります。
直線\(l \ \)は、
2点\(A, \ B \ \)を通り、
直線\(m \ \)は、
関数\( \ y=3x-5 \ \)
のグラフです。
点\(C \ \)は直線\(m \ \)と
\(x \ \)軸の交点、点\(D \ \)は直線\(m \ \)と\(y \ \)軸の交点です。
直線\(m \ \)上に、\(x \ \)座標が
\(x \gt 3 \ \)である点\(P \ \)をとり、
直線\(OP \ \)と直線\(l \ \)の交点を\(Q \ \)とします。
\(\triangle OBQ \ \)の面積と\(\triangle APQ \ \)の面積が等しくなるとき、
点\(P \ \)の\(x \ \)座標を求めなさい。
解答
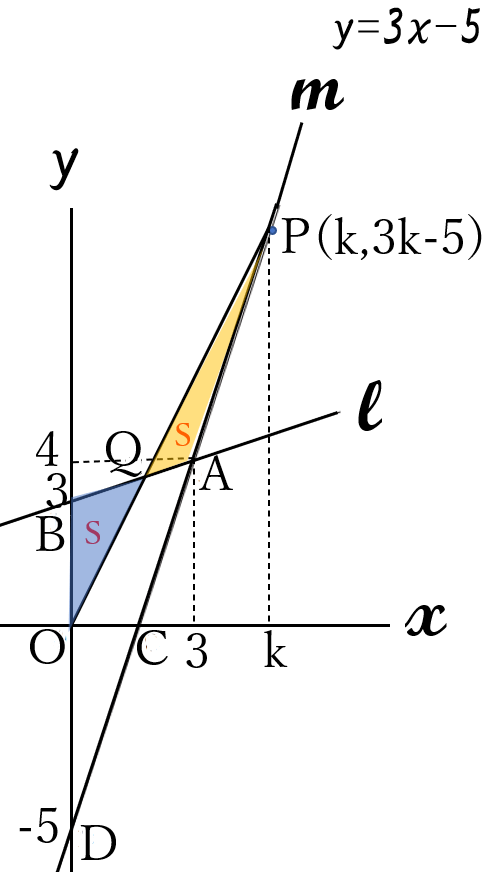
(答) \(\Large \frac{24}{5}\)
求める点\(P \ \)の
\(x \ \)座標を\(k \ \)とします。
\(\triangle OBQ =\triangle APQ\)
だから
\(\triangle DOP=\triangle DBA\)
よって、\(\large \frac{5}{2}k\)\(=12\)
\(\large k=\frac{24}{5}\)
\(\triangle DOP=\triangle DBA\) に気がつけば、上のように簡単に計算できます。暗算での計算も可能です。
問題36
下の図のように、1辺の長さが\(4 \ cm\)の立方体にちょうど入る大きさの球があります。
この球の体積と表面積を求めなさい。
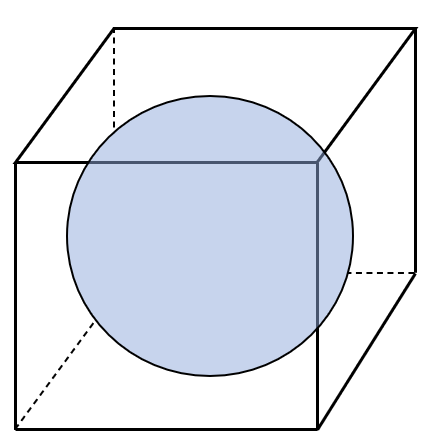
公式を確認しておきましょう!
解答
(答) 体積\(\ \large \frac{32}{3}\pi\) \((cm^3)\) 表面積\( \ \large 16\pi\) \((cm^2)\)
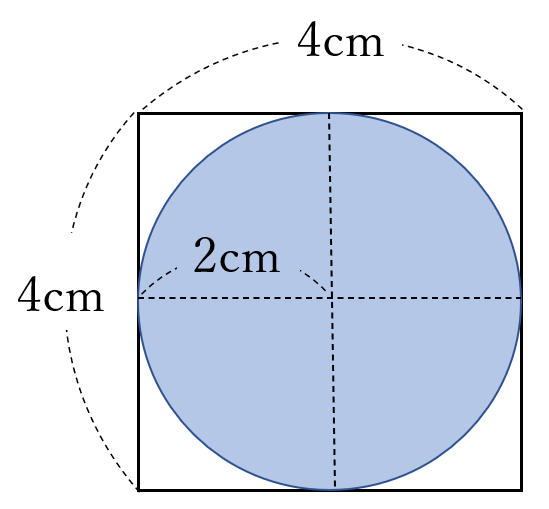
この球の半径は、\(2 \ cm\)
よって、求める球の体積は
\(\Large \frac{4}{3}\pi r^3\)\(\large =\frac{4}{3}\pi 2^3 =\frac{32}{3}\pi\)
求める球の表面積は
\(\Large 4\pi r^2\)\(\large =4\pi 2^2=16\pi\)
前問の類題です。
問題30
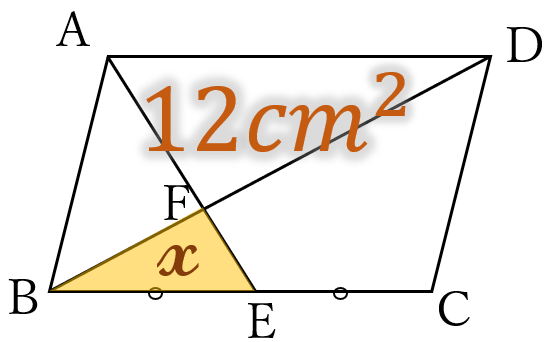
平行四辺形\(ABCD \ \)において、辺\(BC \ \)の中点を\(E\)、線分\(AE \ \)と対角線\(BD \ \)との交点を\(F \ \)とします。
平行四辺形\(ABCD \ \)の面積が\(12cm^2 \ \)のとき、\(\triangle FBE \ \)の面積\(\large \ x \ \)を求めてください。
解答
(答) \(\Large 1\) \((cm^2)\)
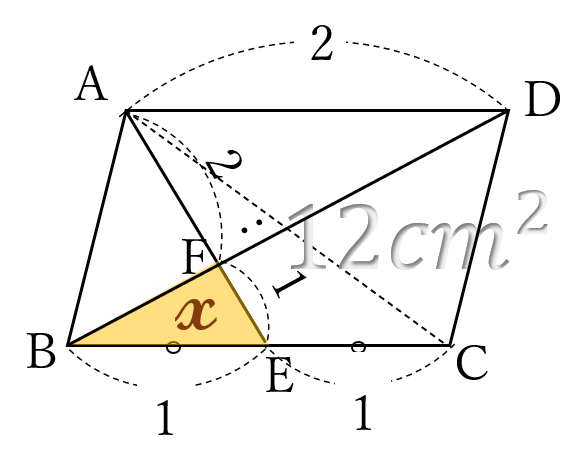
\(\triangle FAD \ \)∽\( \ \triangle FEB, \ AD:EB=2:1\)より
\(FA:FE=2:1\) ここで、
\(\triangle ABC = 平行四辺形ABCD \times \)\(\large \frac{1}{2}\)\(=12\times \)\(\large \frac{1}{2}\)\(=6\)
だから
\(\large x\)\((\triangle FBE) = \triangle ABC \times\)\(\large \frac{BE}{BC}\)\( \times \)\(\large \frac{FE}{AE}\)
\(=6\times \)\(\large \frac{1}{2}\)\( \times \)\(\large \frac{1}{3}=1\)
上の計算は、
\(\triangle ABC\)
\(\rightarrow \triangle ABE\)
\(\rightarrow \triangle FBE\)
の順で
「辺と辺の長さの比」
をかけてます。
問題43
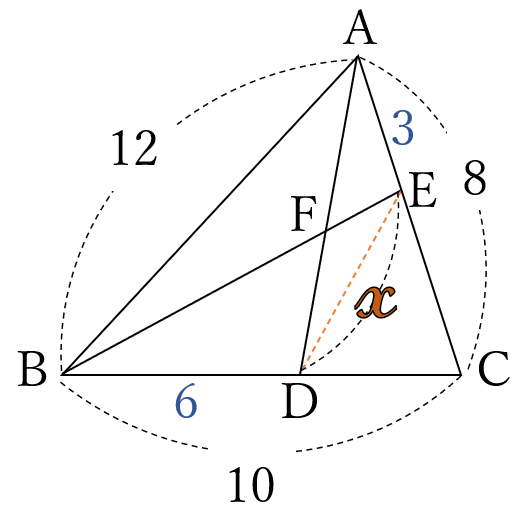
\(\triangle ABC \ \)において、
\(AB=12, \ BC=10, \ CA=8\) です。
辺\(BC \ \)上に\(BD=6 \ \)となる点\(D \ \)をとり、
辺\(AC \ \)上に、\(AE=3 \ \)となる点\(E \ \)をとります。
\(AD \ \)と\( \ BE \ \)の交点を\(F \ \)とするとき、\(DE \ \)の長さ\(\large \ x \ \)を求めてください。
解答
(答) \(\Large 6\)
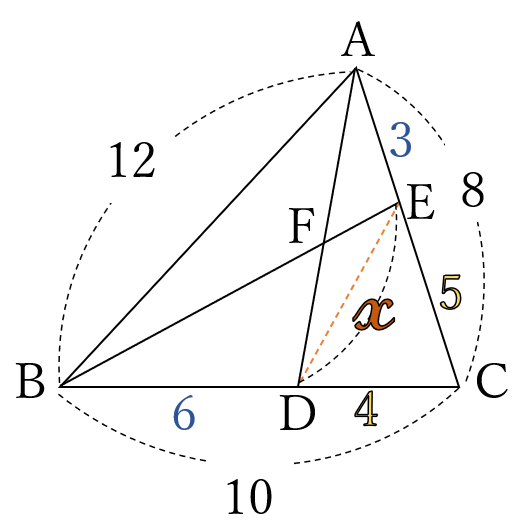
\(\triangle ABC \ \)と\( \ \triangle DEC\)
において
\(AC:BC=4:5\)
\(DC:EC=4:5\)
\(\angle C \ \)は共通だから、2組の辺の比とその間の角が等しいので、\(\triangle ABC \ \)∽\( \ \triangle DEC\)
相似比は\(AC:DC=2:1 \ \)なので
\(\large x\)\((DE)\)\(\large =\frac{1}{2} AB=6\)
前問の続きです。計算というよりは発見です。
問題44
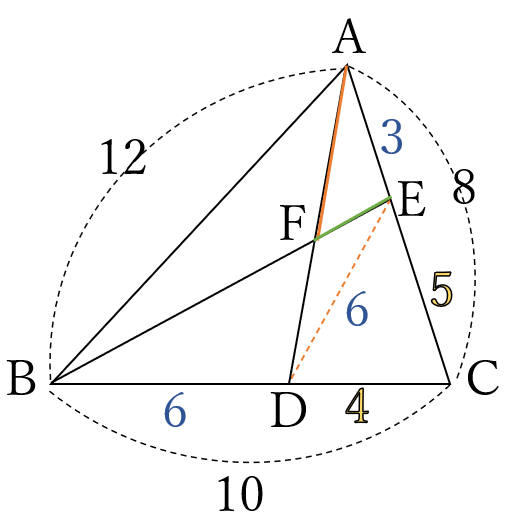
\(AB=12, \ BC=10\)
\(CA=8\) です。
\(\triangle ABC \ \)において、
辺\(BC \ \)上に\(BD=6\)
となる点\(D \ \)をとり、
辺\(AC \ \)上に、
\(AE=3 \ \)となる
点\(E \ \)をとります。
\(AD \ \)と\( \ BE \ \)の
交点を\(F \ \)とするとき、
\(AF:FE\ \ \)を求めてください。
前問より、\(DE=6 \ \)です。
解答
(答) \(\Large AF:FE=2:1\)
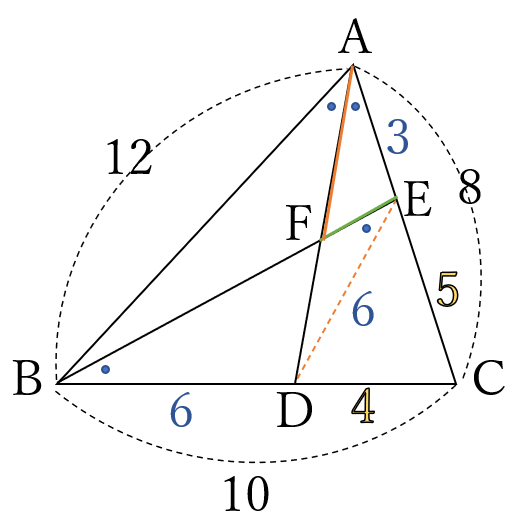
条件より、
\(DC=4, \quad EC=5\)
\(\triangle ADC \ \)∽\( \ \triangle BEC\)
(証明略)\((\ast)\) だから
\(\angle DAC=\angle EBC \ \cdots \ \)①
\(\triangle BDE \ \)は、
\(\angle DEB =\angle DBE \ \cdots \ \)②
の二等辺三角形。さらに
\(AB:AC=BD:DC\)
\(=3:2 \ \)だから\(AD\)は\(\angle BAC \ \)の二等分線
したがって、\(\angle BAD=\angle DAC \ \cdots \ \)③
①②③より \(\angle BAD=\angle DEB\) ゆえに
\(\triangle BAF \ \)∽\( \ \triangle DEF \ \)(証明略)\((\ast \ast)\)
したがって\( \ AF:FE=AB:DE=12:6\)\(\large =2:1\)
\((\ast)(\ast \ast) \ \)の証明は次ページ⇒
証明

\((\ast) \ \triangle ADC \ \)と\( \ \triangle BEC\)
において
\(AC:DC=2:1\)
\(BC:EC=2:1\)
\(\angle ACB\) は共通。
よって2組の辺の比と
その間の角が等しいので
\(\triangle ADC \ \)∽\( \ \triangle BEC \ \)
\((\ast \ast) \ \triangle BAF \ \)と\( \ \triangle DEF\)
において、\(\angle BAF=\angle DEF, \quad \angle AFB=\angle EFD \ (対頂角)\)
2組の角が等しいので\(\triangle BAF \ \)∽\( \ \triangle DEF \ \)
