東京都の問題は、昨年と今年の問題を拝見している。大問が5つあり、すべてに的確に解答するのはかなり難しいと思われる。今回の問題に関しては、問題3⃣の〔問3〕が厄介だ。あと、四角錐の体積問題が2年連続で出題されている。今回の四角錐の体積は比較的求めやすい。
では、大問3⃣の〔問3〕から

〔問3〕の解答例
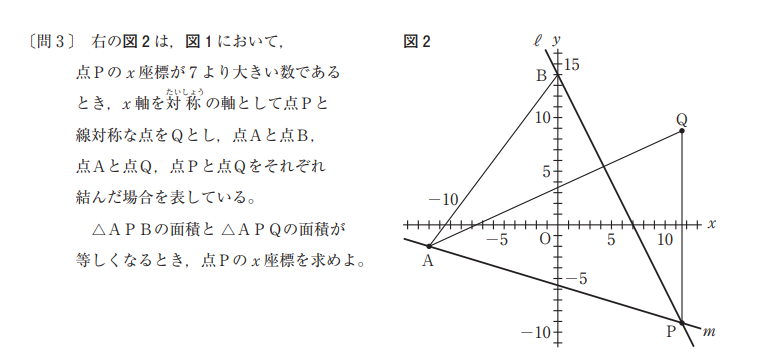
\(A(-12,-2), \quad l:y=-2x+14\)
\(B(0,14)\)
点\(P\)の\(x\)座標を\(a,\quad (a \gt 7)\)とおくと
\(P(a,-2a+14),\quad Q(a,2a-14)\)
\(\triangle APB= \triangle APQ \iff BQ//AP\)
\( \iff \)直線\(AP\)と直線\(BQ\)の傾きは等しい
\(\iff \frac{-2a+14+2}{a+12}=\frac{2a-14-14}{a}\)
\(\iff a(-2a+16)\)
\(=(a+12)(2a-28)\)
\(\iff -2a^2+16a\)
\(=2a^2-4a-12 \times 28\)
\(\iff 4a^2-20a-12 \times 28=0\)
\(\iff a^2-5a-84=0\)
\(\iff (a-12)(a+7)=0\)
\(\iff a=12 \quad (a \gt 7)\)
(答)求める点\(P\)の\(x\)座標は \(12\)
【参考】
\(\triangle APB =\triangle PAQ\)
\(\iff \triangle APB \equiv \triangle PAQ\)
これが検証できれば
\(AB=PQ\) から
以下のように答えが導かれる
\(AB=\sqrt{12^2+(14+2)^2}\)
\(=\sqrt{400}=20\) だから
\(PQ=20\)
\(\iff {2a-14-(-2a+14)}=20\)
\(\iff 4a-28=20\)
\(\iff a=12\)
(答)求める点\(P\)の\(x\)座標は \(12\)
大問4⃣

〔問2〕② 解答例
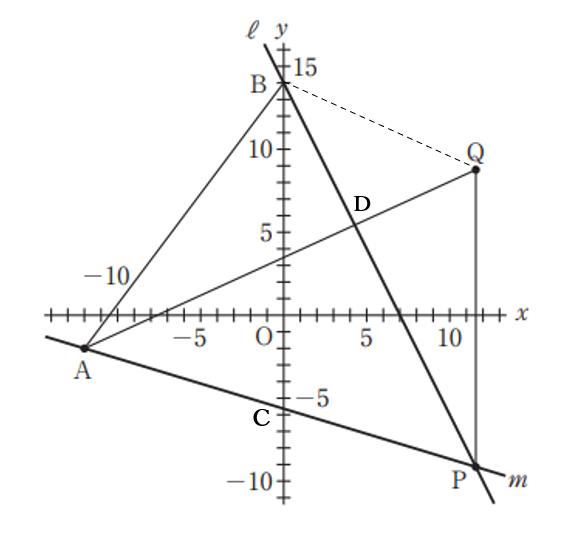
題意より
\(\triangle ABC \sim \triangle BEC \sim \triangle CER\)
\(AB=16,AD=BC=8\)より\(AC=8 \sqrt{5}\)
\(\iff \)
\(BE:EC:BC=2:1:\sqrt{5}\)
よって
\(BC:BE=\sqrt{5}:2\)
\(\iff 8:BE=\sqrt{5}:2\)
\(\iff BE=\frac{16}{\sqrt{5}}\)
\(\iff EC=\frac{8}{\sqrt{5}}\)
\(\iff ER=\frac{4}{\sqrt{5}}\)
面積
\(\triangle BEC = \frac{1}{2} \times BE \times EC\)
\(=\frac{1}{2} \times \frac{16}{\sqrt{5}} \times \frac{8}{\sqrt{5}}=\frac{64}{5}\)
\(\triangle CER=\frac{1}{2} \times EC \times ER\)
\(=\frac{1}{2} \times \frac{8}{\sqrt{5}} \times \frac{4}{\sqrt{5}}=\frac{16}{5}\)
\(\triangle BEC \equiv \triangle PEC\)だから
\(\triangle PEC=\frac{64}{5}\)
\( \iff\)
\( \triangle PRC=\triangle PEC-\triangle CER\)
\(=\frac{64}{5}-\frac{16}{5}=\frac{48}{5}\)
(答) \(\displaystyle \frac{48}{5}\)
【別解】
慣れてくると、相似比を使って一気に計算できます。
\(\triangle ABC \sim \triangle BCE \sim \triangle CER\)
なので相似比は
\(AC:BC:CR=1:\frac{1}{\sqrt{5}}:(\frac{1}{\sqrt{5}}\cdot \frac{1}{2})\)
また
\(\triangle BCE \equiv \triangle CPE\)より
\(\triangle PRC=\triangle BCE-\triangle CRE\)
\(\triangle ABC=64\)
以上より
\(\triangle PRC=\triangle BCE-\triangle CRE\)
\(=\triangle ABC \times (\frac{1}{\sqrt{5}})^2\)
\(-\triangle ABC \times (\frac{1}{\sqrt{5}})^2 \times (\frac{1}{2})^2\)
\(=64\times (\frac{1}{\sqrt{5}})^2\times (1-\frac{1}{4})\)
\(=\frac{64}{5}\times \frac{3}{4}\)
\(=\frac{48}{5}\)
(答) \(\displaystyle \frac{48}{5}\)
大問5⃣

〔問2〕解答例
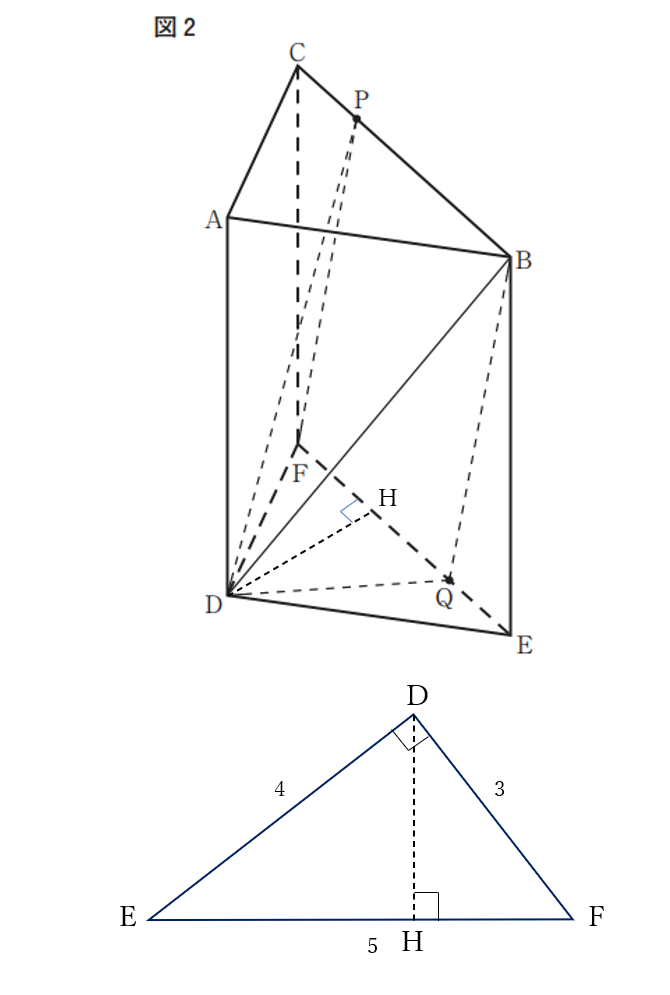
立体\(D-BPFQ\) は、\(D\)を頂点とする四角錐
\(BP=4 \iff FQ=4\)
四角形\(BPFQ\)は平行四辺形だから、
四角形\(BPFQ\)の面積は、\(4 \times 6=24\)
\(\triangle DEF\)の頂点\(D\)から辺\(EF\)に下した垂線の足を\(H\)とすると
\(\triangle DEF \sim \triangle HDF\)
\( \iff DH=3\times \frac{4}{5}=\frac{12}{5}\)
求める立体\(D-BPFQ\)の体積は、
(四角形\(BPFQ\)の面積)\(\times DH \times \frac{1}{3}\)
\(=24 \times \frac{12}{5} \times \frac{1}{3}=\frac{96}{5}\)
(答) \(\displaystyle \frac{96}{5}\)
今回のこの四角錐の高さは、比較的求めやすいので、昨年の四角錐の体積問題よりは解きやすくなっている。