難解な問題は少ないが、思考を要する問題は、大問5⃣の3と大問6⃣の3だろうか。どちらも複雑な計算はないが、落ち着いて慌てずに解く必要がある。
大問5

大問5⃣3の解答例
この問題は、公共交通機関のダイヤグラムに似ている。
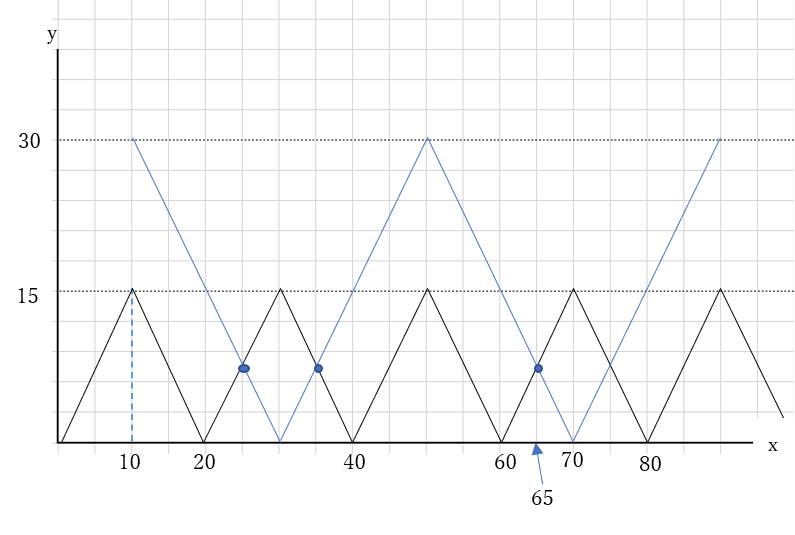
解答は右のグラフのとおりと言ってしまえばそれまでだが、四角形\(BCSR\)の面積を\(t\)の式で表す問題ではない。グラフ上で考える。
点\(R,S\)は10秒後にそれぞれ点\(A,B\)を、秒速0.5cmでスタートとするから、四角形\(BCSR\)の面積は\(30cm^2\)から減少していき、20秒後(\(P,Q\)がスタートして30秒後)に0になる。その後、面積は徐々に増えていき、さらに20秒後に\(30cm^2\)になる。その繰り返しだから、四角形\(BCSR\)の面積と\(t\)(\(x\))の関係は右のグラフのようになる。
二つのグラフの交点で\( \triangle APQ \)の面積と四角形\(BCSR\)の面積は等しくなるので、小さいほうから3番目の\(t\)の値は、65
(答) 65
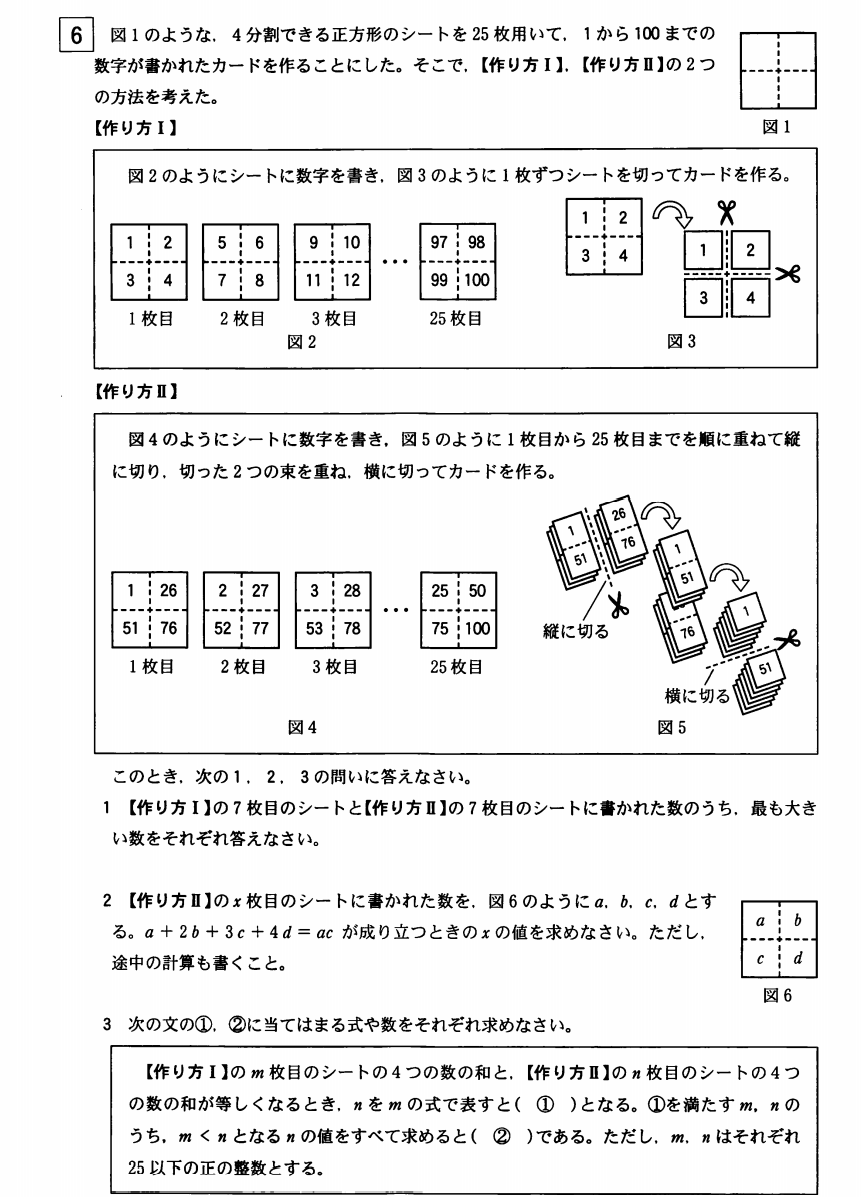
次は、大問6⃣
最近はやりの規則性の問題である。
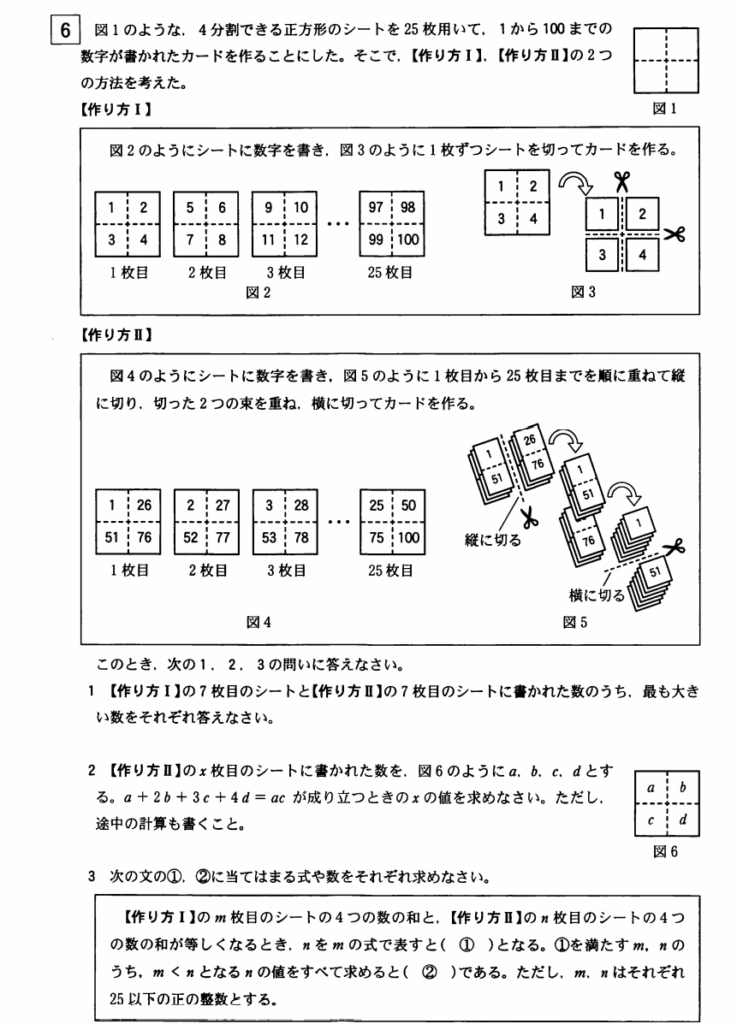
大問6⃣3の解答例
作り方Ⅰの\(m\)枚目、作り方Ⅱの\(n\)枚目の4つの数を\(m,n\)の式で表すと下の図のようになる。
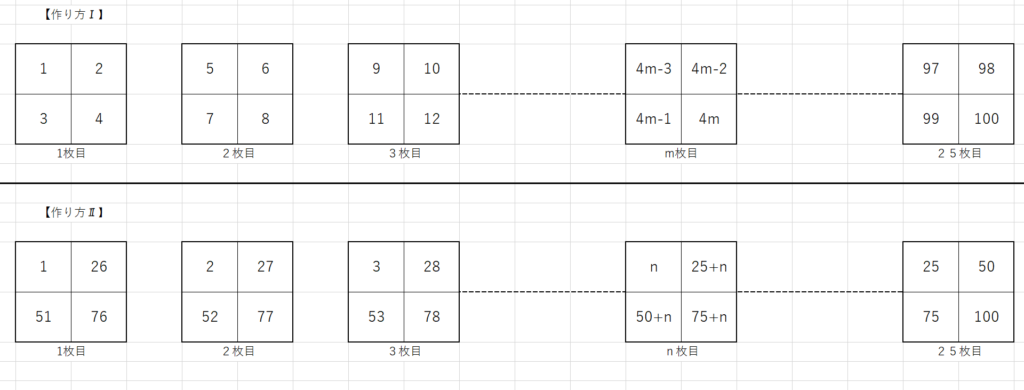
よって、作り方Ⅰの枚目のシートの4つの数と、作り方Ⅱの枚目のシートの4つの数の和が等しくなるとき$$ \begin{eqnarray} (4m-3)+(4m-2)+(4m-1)+4m \\ =n+(25+n)+(50+n)+(75+n) \end{eqnarray}$$ $$ \begin{eqnarray} &\iff& 16m-6=4n+150 \\ &\iff& n=4m-39 \end{eqnarray}$$ ①(答) \(n=4m-39\)
次に、①を満たす\(m,n\)のうち、\(m \lt n \)となる \(n\)の値を求める。
①を変形して$$ n=4(m-10)+1 $$ よって、\(n\) は4の倍数に1を加えた数だから、\(n=25,n=21,n=17,n=13\)などを代入してみる。
\(n=25\)のとき、\(m=16\) 適する
\(n=21\)のとき、\(m=15\) 適する
\(n=17\)のとき、\(m=14\) 適する
\(n=13\)のとき、\(m=13\) 不適
\(n=9\)のとき、\(m=12\) 不適
・・・
② (答) \(n=17, \quad 21, \quad 25\)