問題数が多い。50分という時間の中ですべての問題をそつなく解くことはかなり難しいと思われる。2次関数を含め、図形問題の解法に多少時間がかかるだろう。
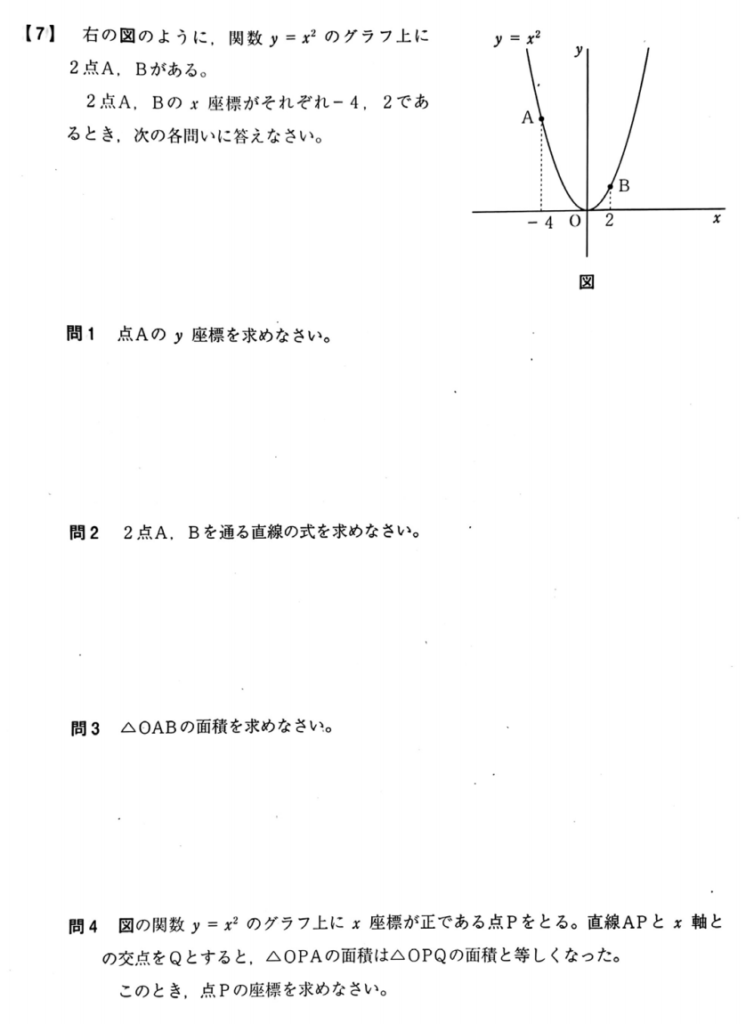
大問【7】
問3 解答例
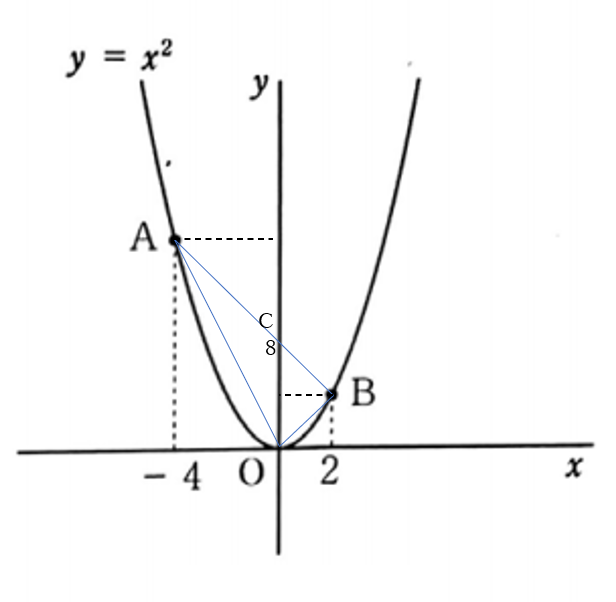
よくある面積問題である。この機会に解き方を覚えてしまおう。
問2より
\(AB\)の方程式は
\(y=-2x+8\)
直線\(AB\)と\(y\)軸との交点を\(C\)とすると
\(C(0,8)\)
求める\(\triangle OAB\)の面積を
\(OC\)を底辺とした二つの三角形の和
として計算すると計算が楽になる。
\(\triangle OAB=\triangle OCA+ \triangle OCB\)
\(=OC\times 4 \times \frac{1}{2} + OC\times 2 \times \frac{1}{2}\)
\(=OC\times (4+2) \times \frac{1}{2}\)
\(=8\times 6\times \frac{1}{2}\)
\(=24\)
問3 (答) \(24\)
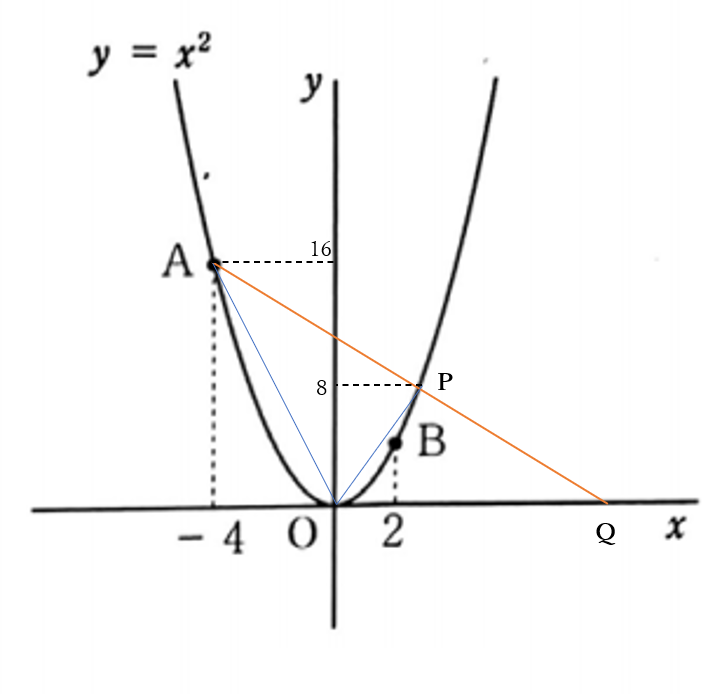
問4 解答例
\(\triangle OPA=\triangle OPQ\)
\(\iff \triangle OPQ=\frac{1}{2} \triangle OAQ\)
よって\(\triangle OPQ\)の高さは
\(\triangle OAQ\)の高さの\(\frac{1}{2}\)である。
よって\(P\)の\(y\)座標は\(8\)
\(x \gt 0\)だから
\(x^2=8 \iff x=2\sqrt{2}\)
問4 (答) \(P(2\sqrt{2},8)\)
大問【8】

問3 解答例
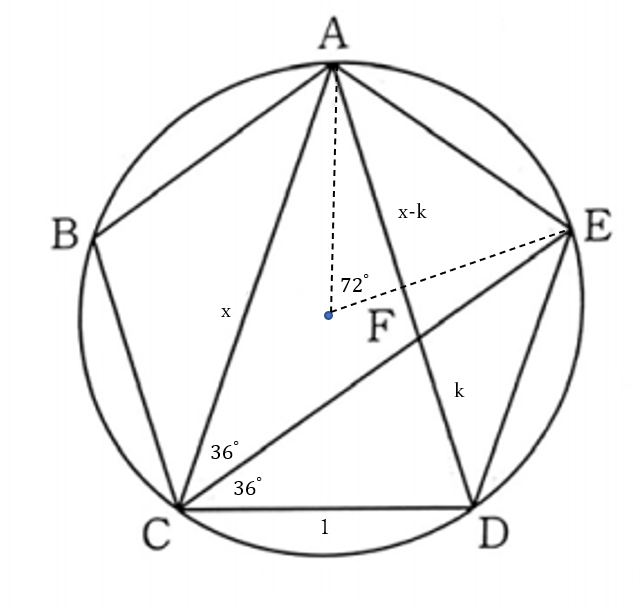
右の図のように
\(AD=AC=x \quad (x \gt 0)\)
\(FD=k\) とおくと
\(AF=x-k\)
\(\triangle ACD \sim \triangle CDF\) だから
\(AC:CD=CD:DF\)
\(\iff x:1=1:k\)
\(\iff k=\frac{1}{x}\cdots\)①
\(CE\)は\(\angle ACD\)の二等分線だから
\(CD:CA=DF:FA\)
\(\iff 1:x=k:(x-k)\)
\(\iff kx=x-k\cdots\)②
①②より
\(1=x-\frac{1}{x}\)
\(\iff x^2-x-1=0\)
\(\iff x=\frac{1+\sqrt{5}}{2}\)
問3 (答) \(\large \frac{1+\sqrt{5}}{2}\) \((cm)\)
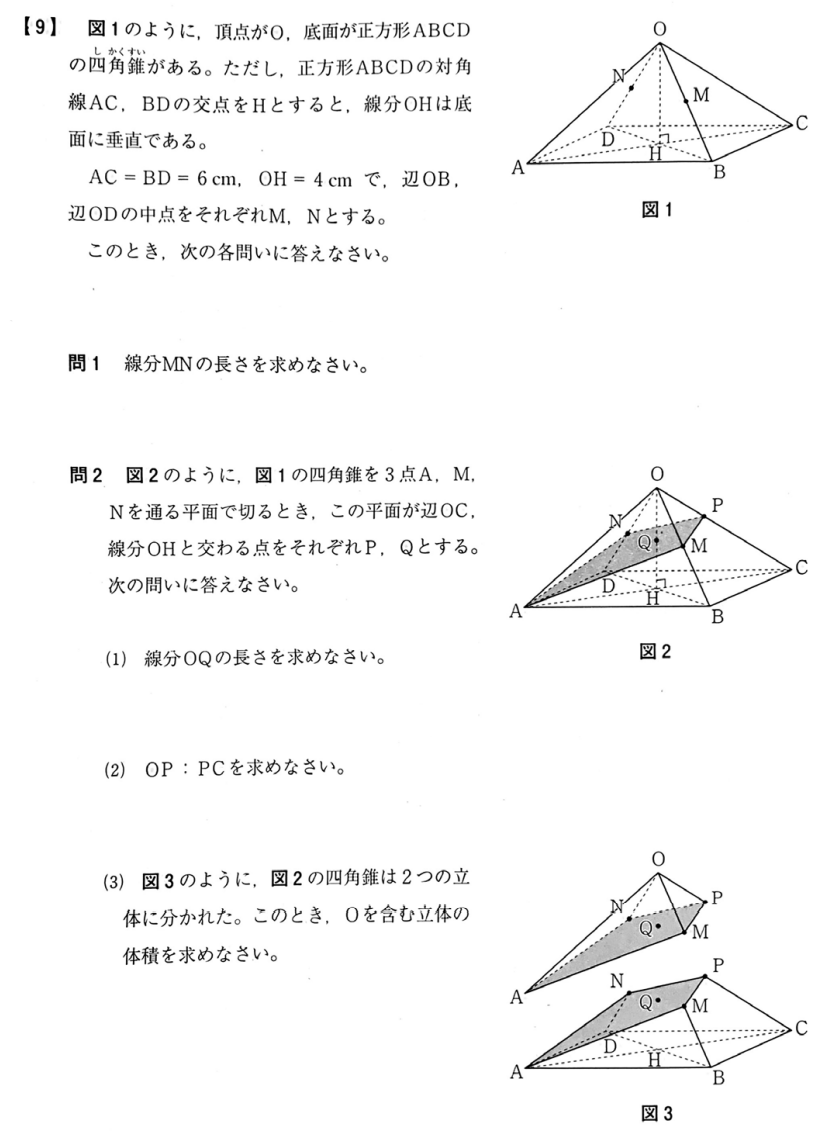
大問【9】
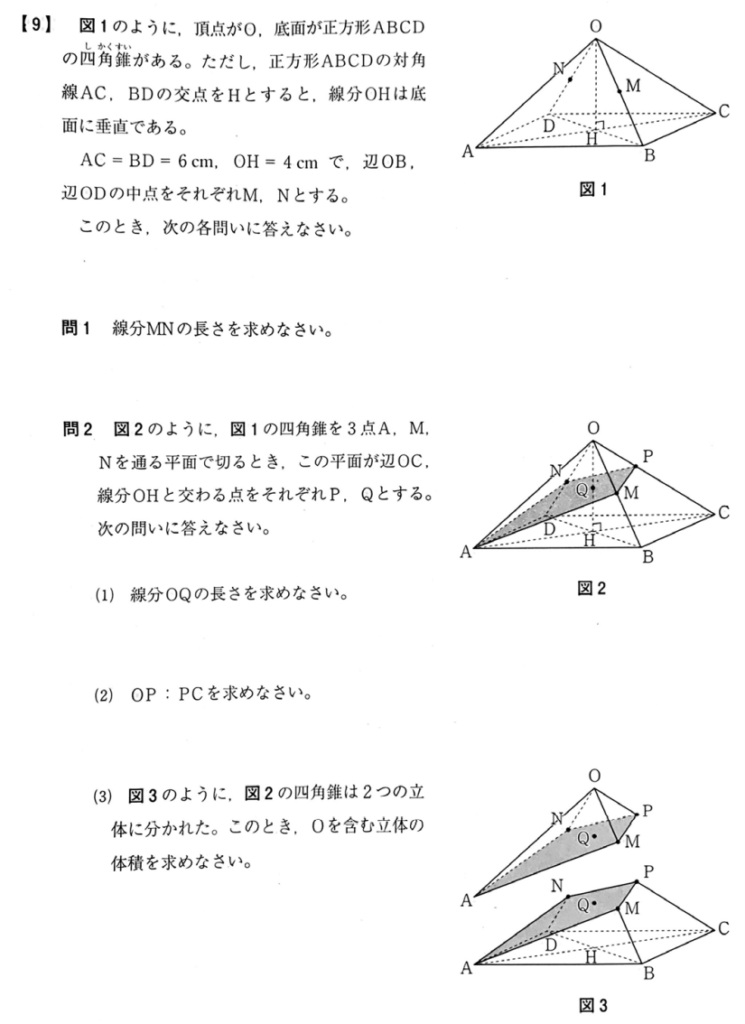
問1解答例
(1)
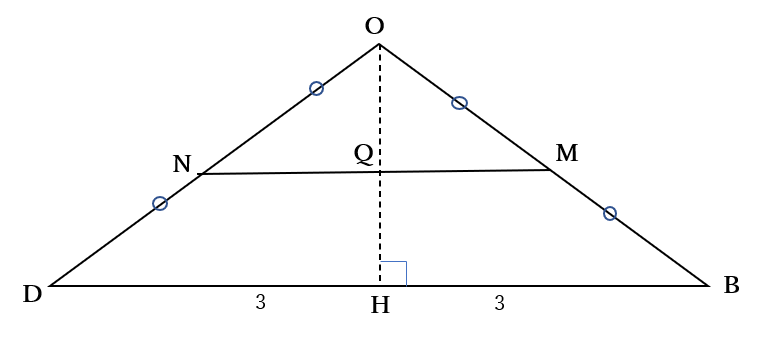
中点連結定理より
\(MN=\frac{1}{2}BD\)
\(=\frac{1}{2}\cdot 6=3\)
(1) (答) \(3\)
(2)
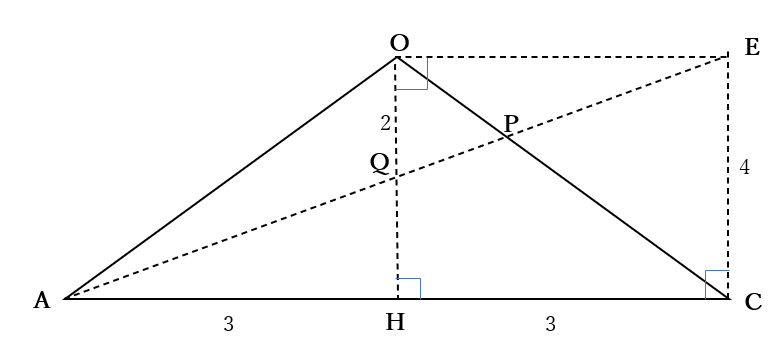
\(AN=AM,PM=PN\)だから
\(A,Q,P\)は一直線上にある。
右の図のように
点\(C\)を通り直線\(AC\)に垂直な直線をひき
この直線と直線\(AP\)との交点を\(E\)とおくと
\(CE=4\)
\(\triangle POQ \sim \triangle PCE\)ゆえ
\(OP:PC=OQ:CE=1:2\)
(2) (答) \(OP:PC=1:2\)
(3)
\(P\)から直線\(AC\)におろした垂線の足を\(F\)とする
\(OP:PC=1:2, \ HC=3\)より
\(HF=1\)
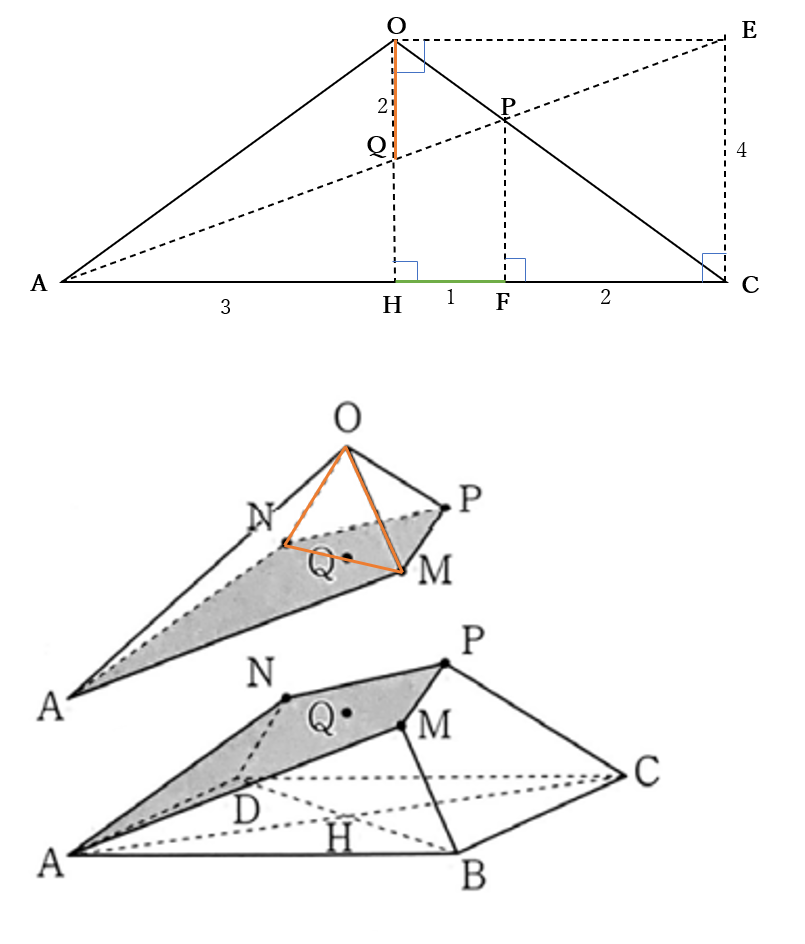
求める立体の体積は
\(\triangle OMN\)を底面とする二つの三角錐
\(A-OMN\)の体積と\(P-OMN\)の体積の和である
\(\triangle OMN\)は正方形\(ABCD\)に垂直であるから
三角錐\(A-OMN\)の高さは\(AH=3\)
三角錐\(P-OMN\)の高さは\(HF=1\)である
\(\triangle OMN=\frac{1}{2}MN\cdot OQ\)
\(=\frac{1}{2}\cdot 3\cdot 2=3\) だから
三角錐\(A-OMN\)の体積は
\(3\times AH\times \frac{1}{3}\)
\(=3\times 3\times \frac{1}{3}=3\)
三角錐\(P-OMN\)の体積は
\(3\times FH\times \frac{1}{3}\)
\(=3\times 1\times \frac{1}{3}=1\)
よって求める立体の体積は
\(3+1=4\)
(3) (答) \(4\) \((cm^3)\)