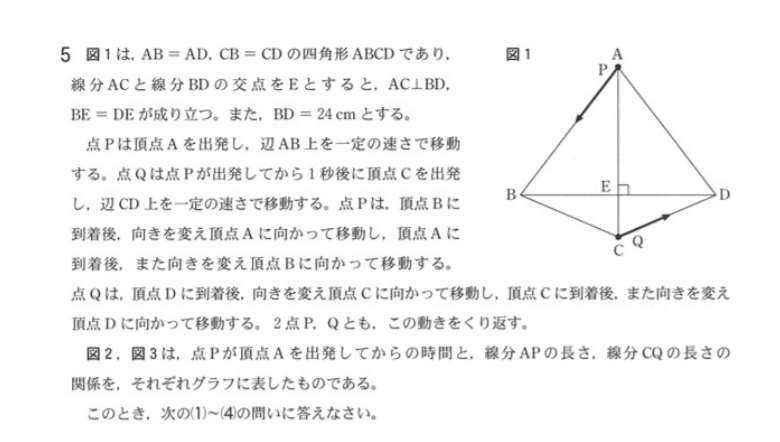
今回の問題で、受験生を苦しめたのが大問5の(4)②ではないだろうか。
問題の下に、一応、解答を示しておきました。参考にしてください。
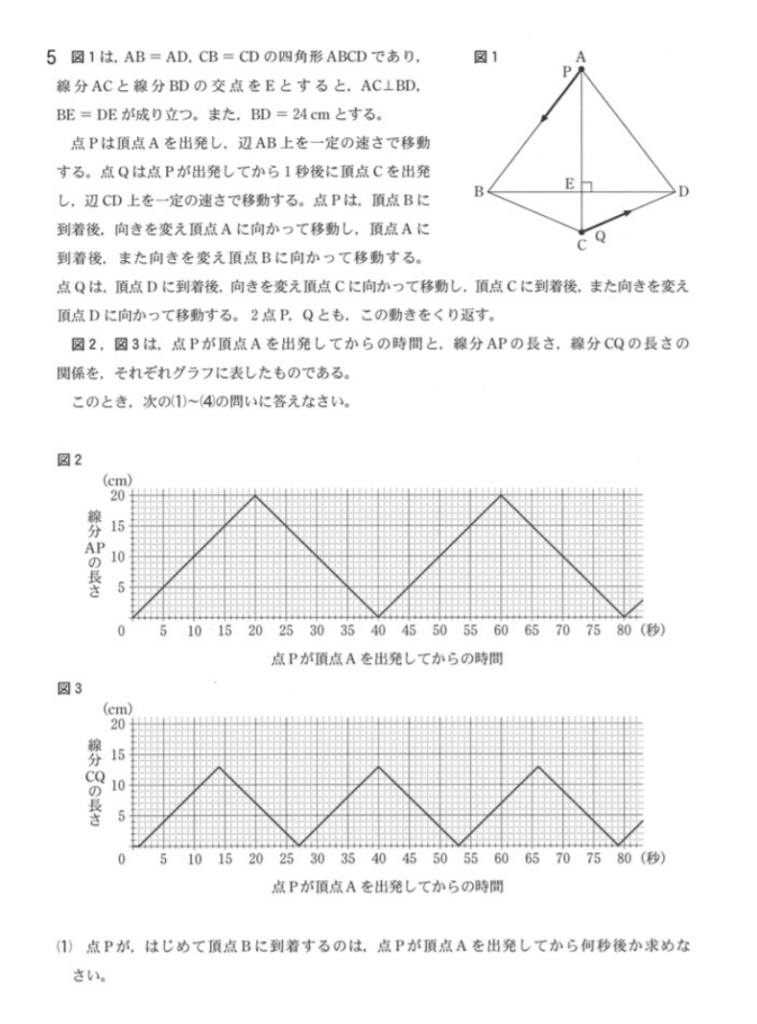

大問5の(4)② 解答例
《考え方》
⊿APCと⊿AQCの底辺をACとすれば、底辺は共通であるから、
「面積が等しい⇔高さが等しい」
したがって、
⊿APCの高さを\(PH\)、⊿AQCの高さを\(QH’\)とおいて、それぞれを\(x\)の式で表して、\(PH=QH’\)から、\(x\)の一次方程式を解けばよい。
このことに気が付けば、あとは計算だけである。
解法の障害となるのが、高さ\(PH\)と\(QH’\)を\(x\)の式で表すこと。とくに\(QH’\)はやっかいである。また、\(PH=QH’\)からの\(x\)についての一次方程式の計算がちょっとてこずる。計算慣れしていないと計算ミスにつながる。
・・・・・・・・・・・・・・・・・・・・
大問5(3)までに解っている事柄
\(AB=AD=20cm,CD=CB=13cm\),
\(EB=ED=12cm,AC=21cm\)
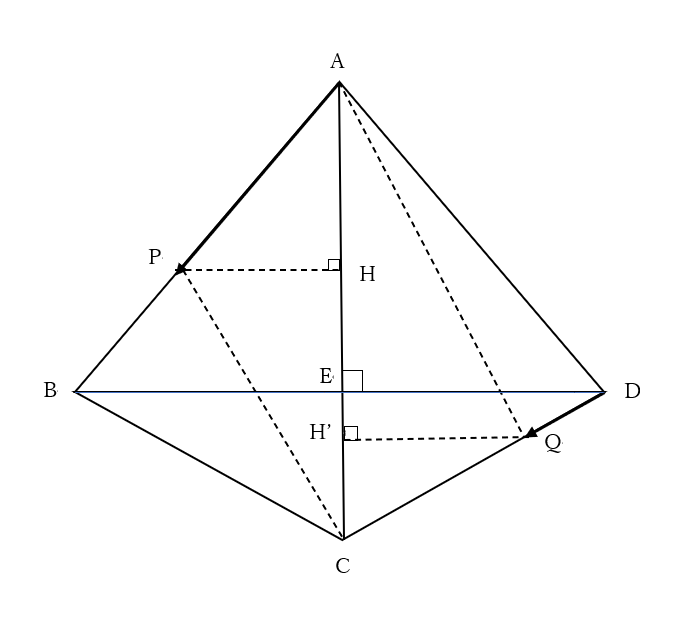
また、\(14\le x\le 20\)だから、点PはAからBに向かって、点QはDからCに向かって動いてる。
したがって\(x\)秒後、\(AP=x,DQ=x-14\)
点PからACに下した垂線の足をHとすると、⊿ABE∽⊿APHだから相似比より
\(AB:BE=AP:PH\) よって、\(20:12=x:PH⇔PH=\frac{3}{5}x\)
(①で既に計算済み)
点QからACに下した垂線の足をH’とすると、⊿CDE∽⊿CQH’だから相似比より
\(DC:DE=QC:QH’\) よって、\(13:12=QC:QH’\) ここで、
\(QC=13-DQ=13-(x-14)\)
\(=27-x\) ゆえ
\(13:12=(27-x):QH’\)
⇔ \(13QH’=12(27-x)\)
⇔ \(QH’=\frac{12(27-x)}{13}\)
⊿APCと⊿AQCの底辺ACは共通だから、
\(S=T⇔PH=QH’\) よって \(\frac{3}{5}x=\frac{12(27-x)}{13}\)
これを解いて、\(x=\frac{180}{11}\)
(補足)
\(\frac{3}{5}x=\frac{12(27-x)}{13}\)を解くとき、いきなり展開してはいけない。
計算が楽になるように工夫しよう。
\(\frac{3}{5}x=\frac{12(27-x)}{13}\)の両辺を見ると、左辺に3が右辺に12がかけられているので、
まず、両辺を、3と12の最大公約数の3で割る。 \(\frac{1}{5}x=\frac{4(27-x)}{13}\)
分数のまま計算するとめんどくさくなるで、両辺の分母を見て、
左辺の分母5と右辺の分母13を両辺にかける。(5と13の最小公倍数をかける。)
\(13x=20(27-x)\) これで解きやすくなったけど、展開して
\(33x=20\times27\) 、20と27をそのままかけないで
\(x=\frac{20\times3\times9}{3\times11}=\frac{180}{11}\)
ちょっとした工夫で計算は楽になります。